Равносильные преобразования формул
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой. Формулы можно упрощать с помощью определенных правил.
Законы алгебры логики:
1.Коммутативность
относительно конъюнкции относительно дизъюнкции
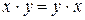
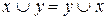
2.Ассоциативность
относительно конъюнкции относительно дизъюнкции
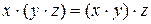
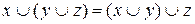
3.Дистрибутивность
конъюнкции относительно дизъюнкции относительно
дизъюнкции конъюнкции
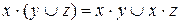
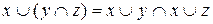
4.Законы де Моргана
относительно конъюнкции относительно дизъюнкции
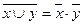
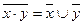
5.Закон поглощения
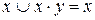
6.Законы идемпотентности
относительно конъюнкции относительно дизъюнкции

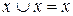
7.Законы противоречия
относительно конъюнкции относительно дизъюнкции
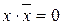
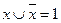
8.Законы действие с константами
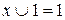
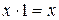
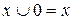
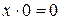
Одни операции можно выразить через другие: импликация выражается через дизъюнкцию и отрицание, эквиваленция – через отрицание, дизъюнкцию и конъюнкцию:
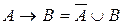 ,
, 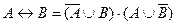 ,
,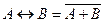 ,
, 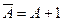 .
.
Таким образом, операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания. Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок считается, что сначала выполняется операция отрицания («не»), затем конъюнкция («и»), после конъюнкции – дизъюнкция («или») и в последнюю очередь – импликация.
Пример 1. Упростить формулу 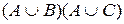 .
.
Решение:
а) Раскроем скобки:
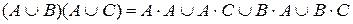 .
.
б) По закону идемпотентности
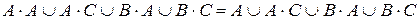 .
.
в) Из высказываний  и
и 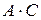 вынесем за скобки
вынесем за скобки 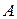 и, используя законы констант, получим:
и, используя законы констант, получим: 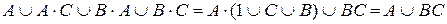 , таким образом, мы доказали закон дистрибутивности.
, таким образом, мы доказали закон дистрибутивности.
Всякую формулу  можно преобразовать так, что в ней не будет отрицаний сложных высказываний – все отрицания будут применяться только к простым высказываниям.
можно преобразовать так, что в ней не будет отрицаний сложных высказываний – все отрицания будут применяться только к простым высказываниям.
Пример 2.Преобразовать формулу 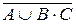 так, чтобы не было отрицаний сложных высказываний.
так, чтобы не было отрицаний сложных высказываний.
Решение:
а) воспользуемся формулой де Моргана  ;
;
б) для выражения  применим еще раз формулу де Моргана, получим:
применим еще раз формулу де Моргана, получим: 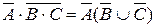 .
.
Любую формулу можно тождественно преобразовать так, что в ней не будут использованы знаки логического сложения или знаки логического умножения, а будут использованы знаки отрицания и логического умножения или знаки отрицания и логического сложения.
Пример 3.
Преобразовать формулу 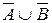 так, чтобы в ней не использовались знаки логического сложения.
так, чтобы в ней не использовались знаки логического сложения.
Решение:
Воспользуемся законом двойного отрицания, а затем формулой де Моргана: 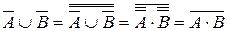 .
.
Пример 4. Преобразовать формулу 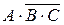 так, чтобы в ней не использовались знаки логического умножения.
так, чтобы в ней не использовались знаки логического умножения.
Решение:
Используя формулы де Моргана и закон двойного отрицания, получим:
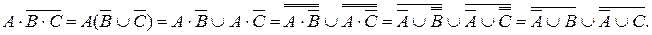 В алгебре логики всякую логическую функцию можно выразить через другие логические функции, но при этом должно быть по меньшей мере две операции, при этом одной из них обязательно должно быть отрицание.
В алгебре логики всякую логическую функцию можно выразить через другие логические функции, но при этом должно быть по меньшей мере две операции, при этом одной из них обязательно должно быть отрицание.
Все операции можно выразить через конъюнкцию и отрицание, дизъюнкцию и отрицание, импликацию и отрицание.
Через эквиваленцию и отрицание остальные операции выразить нельзя.
Упражнения
1. Упростить логические выражения:
a) (A Ù B)Ú(AÙØB);
b) (A Ú B)Ù(ØAÚB);
c) (ХÙY);
d) (XÚY)ÙX;
e) (AÚB);
f) (AÚB)(AÚC)(BÚC);
g) AÙCÚCÙ(BÚC)Ú(AÚB)ÙC;
h) (AÚC)Ù(AÙC)Ù(BÚC)Ù(BÙC).
2. Формулы данных высказываний преобразовать в эквивалентные, исключив логическое сложение:
а) 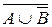 ; б)
; б) 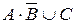 ; в)
; в) 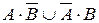 .
.
3. Формулы данных высказываний преобразовать в эквивалентные, исключив логическое умножение:
а) 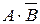 ; б)
; б) 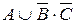 ; в)
; в) 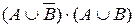 .
.
4. Упростить:
а) 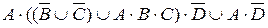 ; б)
; б) 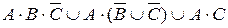 .
.
5. Записать данные высказывания, используя операции логического умножения и отрицания:
a) 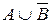 ; б)
; б) 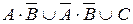 ; в)
; в) 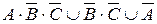 .
.
6. Записать высказывания, используя только операции логического сложения и отрицания:
а) 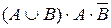 ; б)
; б) 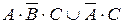 ; в)
; в) 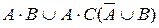 .
.
Дата добавления: 2016-04-11; просмотров: 3790;
