Индивидуальное задание. 6. Привести функцию к ДНФ, затем к СДНФ, с помощью законов алгебры логики:
6. Привести функцию к ДНФ, затем к СДНФ, с помощью законов алгебры логики:
6.1 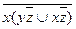 ;
;
6.2 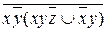 ;
;
6.3 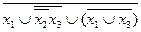 ;
;
6.4 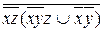 ;
;
6.5 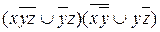 ;
;
6.6 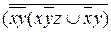 ;
;
6.7 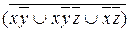 ;
;
6.8 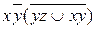 ;
;
6.9 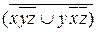 ;
;
6.10 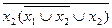 ;
;
6.11 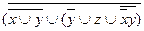 ;
;
6.12 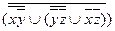 ;
;
6.13 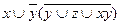 ;
;
6.14 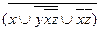 ;
;
6.15 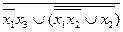 .
.
7. Найти по таблице истинности СДНФ и СКНФ:
7.1 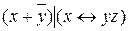 ;
;
7.2 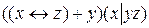 ;
;
7.3 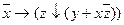 ;
;
7.4 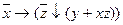 ;
;
7.5 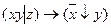 ;
;
7.6 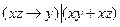 ;
;
7.7 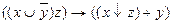 ;
;
7.8 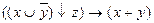 ;
;
7.9 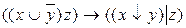 ;
;
7.10 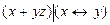 ;
;
7.11 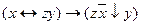 ;
;
7.12 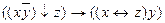 ;
;
7.13 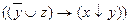 ;
;
7.14 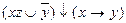 ;
;
7.15 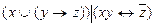 .
.
8. От ДНФ перейти к КНФ, затем к СКНФ:
8.1 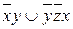 ;
;
8.2 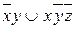 ;
;
8.3 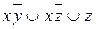 ;
;
8.4 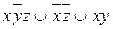 ;
;
8.5 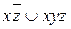 ;
;
8.6 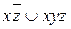 ;
;
8.7 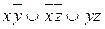 ;
;
8.8 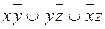 ;
;
8.9 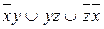 ;
;
8.10 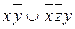 .
.
8.11 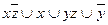 ;
;
8.12 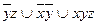 ;
;
8.13 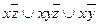 ;
;
8.14 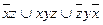 ;
;
8.15 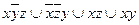 .
.
Сокращенная ДНФ
Любую функцию (кроме тождественного нуля) можно представить в виде СДНФ. На практике часто бывает удобно получить (вместо СДНФ) как можно более “короткую” ДНФ. Словам “короткая ДНФ” можно придать разный смысл, а именно ДНФ называется:
– минимальной, если она содержит наименьшее число букв (среди всех ДНФ ей равносильных);
– кратчайшей, если она содержит минимальное количество знаков дизъюнкции;
– тупиковой, если уничтожение одной или нескольких букв в ней приводит к неравной ДНФ;
– сокращенной ДНФ, если ее упрощение проведено с помощью правила Блейка.
На практике наиболее важной представляется нахождение минимальной ДНФ, но алгоритм ее нахождения по существу является вариантом перебора всех равносильных ДНФ. Проще всего находить сокращенную ДНФ по карте Карно.
Алгоритм получения сокращенной ДНФ по карте Карно:
· составляем таблицу истинности;
· построим таблицу – карту Карно;
· объединяем две рядом стоящие единицы (или 4, 8, 16), наборы (10) и (00) считаются рядом стоящими;
· выписываем строки, соответствующие объединенным единицам одну под другой, к i–му столбцу, в котором повторяются все нули, – переменную 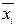 , к столбцу, в котором стоят все единицы, – переменную
, к столбцу, в котором стоят все единицы, – переменную 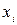 , затем переменные объединить знаком конъюнкции;
, затем переменные объединить знаком конъюнкции;
· все полученные конъюнкции объединяем знаком дизъюнкции, получится сокращенная ДНФ.
Метод Блейка построения сокращенной ДНФ из произвольной ДНФ:
1 этап. Производится операция обобщенного склеивания по формуле 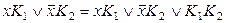 до тех пор, пока это возможно: если среди дизъюнктных слагаемых в ДНФ имеются слагаемые
до тех пор, пока это возможно: если среди дизъюнктных слагаемых в ДНФ имеются слагаемые 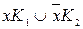 , то ко всей дизъюнкции добавляем слагаемое К1К2, проделываем эту операцию несколько раз (можно последовательно, можно одновременно) для всех возможных пар слагаемых, а затем применяем обычное поглощение.
, то ко всей дизъюнкции добавляем слагаемое К1К2, проделываем эту операцию несколько раз (можно последовательно, можно одновременно) для всех возможных пар слагаемых, а затем применяем обычное поглощение.
2 этап. Производится операция поглощения 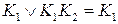 . Операции применяются слева направо: если добавляемое слагаемое уже содержалось в ДНФ, то его можно отбросить совсем, например,
. Операции применяются слева направо: если добавляемое слагаемое уже содержалось в ДНФ, то его можно отбросить совсем, например, 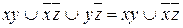 .
.
Пример 1.Сократить ДНФ по правилу Блейка:
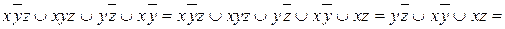
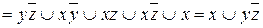 .
.
Пример 2. Сократить функцию по карте Карно:
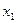
| 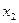
| 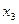
| f |
Составляем карту Карно:
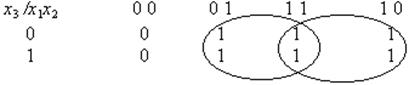
Выписываем строки, соответствующие четырем единицам:
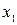
| 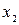
| 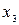
|
Ко второму столбцу выписываем одну переменную – 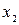 . К следующим четырем единицам выписываем переменную –
. К следующим четырем единицам выписываем переменную – 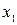 .
.
СДНФ функции содержит (по числу единиц) шесть дизъюнктных слагаемых, но ее сокращенная ДНФ содержит (после объединения единиц) всего две буквы: f = x1  x2.
x2.
Упражнения
1. Сократить функцию по карте Карно:
а)
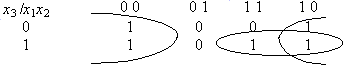
Ответ: 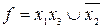 .
.
b)
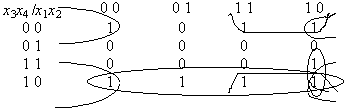
Ответ: 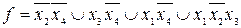 .
.
с)
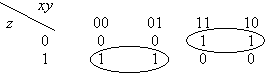
Ответ: f(x, y, z) = 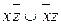 .
.
d)
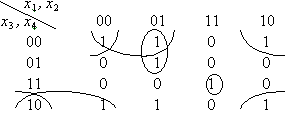
Ответ: f(x, y, z) = 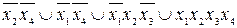 .
.
2.Составить карту Карно и найти сокращенную ДНФ для функций:
a) f(x,y)=(xy 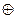
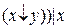 ;
;
b) f(x,y)=((x 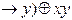 );
);
c) f(x,y)=(x 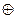 y)
y)  0;
0;
d) f(x,y)=(x 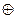 y)
y) 
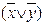 ;
;
e) f(x,y)=(x 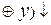 (x
(x  y);
y);
f) f(x,y)=(x  (x
(x 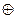 y))(x
y))(x 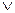 y).
y).
Дата добавления: 2016-04-11; просмотров: 1805;
