Индивидуальное задание. 14 Решить логическую задачу табличным способом или способом упрощения логических функций.
14 Решить логическую задачу табличным способом или способом упрощения логических функций.
14.1 В некотором царстве-государстве повадился Змей Горыныч разбойничать. Послал царь четырех богатырей погубить Змея, а награду за то обещал великую. Вернулись богатыри с победой и спрашивает их царь: «Так кто же из вас главный победитель, кому достанется царева дочь и полцарства?» Засмущались добры молодцы и ответы дали туманные: Сказал Илья Муромец: «Это все Алеша Попович, царь-батюшка». Алеша Попович возразил: «То был Микула Селянинович». Микула Селянинович: «Не прав Алеша, не я это». Добрыня Никитич: «И не я, батюшка». Подвернулась тут баба Яга и говорит царю: «А прав то лишь один из богатырей, видела я всю битву своими глазами». Кто же из богатырей победил Змея Горыныча?
14.2Обсуждая конструкцию нового трехмоторного самолета, трое конструкторов поочередно высказали следующие предположения:
- при отказе второго двигателя надо приземляться, а при отказе третьего можно продолжать полет;
- при отказе первого двигателя лететь можно или при отказе третьего двигателя лететь нельзя; при отказе третьего двигателя лететь можно, но при отказе хотя бы одного из остальных надо садиться. Летные испытания подтвердили правоту каждого из конструкторов. Определите, при отказе которого из двигателей нельзя продолжать полет.
14.3 В соревнованиях по плаванию участвовали Андрей, Виктор, Саша и Дима. Их друзья высказали предположения о возможных победителях: первым будет Саша, Виктор будет вторым; вторым будет Саша, Дима будет третьим; Андрей будет вторым, Дима будет четвертым. По окончании соревнований оказалось, что в каждом из предположений только одно из высказываний истинно, другое ложно. Какое место на соревнованиях занял каждый, если все они заняли разные места.
14.4 Определить, кто из четырех студентов сдал экзамен, если известно:
1) Если первый сдал, то и второй сдал.
2) Если второй сдал, то третий сдал или первый не сдал.
3) Если четвертый не сдал, то первый сдал, а третий не сдал.
4) Если четвертый сдал, то и первый сдал.
14.5 Известно следующее: если Петя не видел Колю на улице, то Коля либо ходил в кино, либо Петя сказал правду; если Коля не ходил в кино, то Петя не видел Колю на улице, и Коля сказал правду. Если Коля сказал правду, то либо он ходил в кино, либо Петя солгал. Выясните, ходил ли Коля в кино.
14.6 Украли у Ивана Царевича Василису Прекрасную. Поехал он выручать ее. Поймал Змея Горыныча, Бабу Ягу, Кощея Бессмертного и Лешего – Иван Царевич знал, что один из них украл ее. И спрашивает: «Кто украл Василису?» Змей Горыныч, Баба Яга и Кощей Бессмертный ответили: «Не я», а Леший – «Не знаю». Потом оказалось, что двое из них сказали правду, а двое – неправду. Знает ли Леший, кто украл Василису?
14.7 Жили-были на свете три поросёнка, три брата: Ниф-Ниф, Наф-Наф, Нуф-Нуф. Построили они три домика: соломенный, деревянный и кирпичный. Все три брата выращивали возле своих домиков цветы: розы, ромашки и тюльпаны. Известно, что Ниф-Ниф живет не в соломенном домике, а Наф-Наф – не в деревянном; возле соломенного домика растут не розы, а тот, у кого деревянный домик, выращивает ромашки. У Наф-Наф аллергия на тюльпаны, поэтому он не выращивает их. Узнайте, кто в каком домике живет и какие цветы выращивает.
14.8 Ирена любит мороженое с фруктами. В кафе был выбор из таких вариантов: пломбир с орехами; пломбир с бананами; пломбир с черникой; шоколадное с черникой; шоколадное с клубникой. В четырех вариантах Ирене не нравились или тип мороженого, или наполнитель, а в одном варианте ей не нравились ни мороженое, ни наполнитель. Она попросила приготовить из имеющихся продуктов порцию по своему вкусу. Какое же мороженое и с какими фруктами любит Ирена?
14.9Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?
14.10В поездке пятеро друзей - Антон, Борис, Вадим, Дима и Гриша знакомились с попутчицей. Они предложили ей отгадать их фамилии, причем каждый из них высказал одно истинное и одно ложное утверждение. Дима сказал: "Моя фамилия - Мишин, а фамилия Бориса - Хохлов". Антон сказал: " Мишин - это моя фамилия, а фамилия Вадима - Белкин". Борис сказал: " Фамилия Вадима - Тихонов, а моя фамилия - Мишин". Вадим сказал: " Моя фамилия - Белкин, а фамилия Гриши - Чехов". Гриша сказал: " Да, моя фамилия - Чехов, а фамилия Антона - Тихонов". Какую фамилию носит каждый из друзей?
14.11 Три ученика, Саша, Коля и Вова, прогуляли информатику. Когда их спросили, кому пришла в голову эта идея, они ответили следующее: Саша: «Я никогда не призывал к прогулу, это была идея Коли». Коля: «Я никогда не предложил бы это первым, во всем виноват Вова». Вова: «Эта идея пришла в голову Коле. Я просто пошел за компанию».
Внутренним чутьем учитель почувствовал, что один ученик говорит правду, второй говорит правду только наполовину, а третий – лжет. Кто из учеников был инициатором прогула? Ответ дайте в виде первой буквы имени.
14.12 В симфонический оркестр приняли на работу трех музыкантов – Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе. Известно, что: (1) Смит – самый высокий
(2) играющий на скрипке меньше ростом играющего на флейте
(3) играющие на скрипке и флейте и Браун любят пиццу
(4) когда между альтистом и трубачем возникает ссора, Смит мирит их
(5) Браун не умеет играть ни на трубе, ни на гобое.
Выясните, на каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами.
14.13Ученицы – Галина, Наташа, Юлия и Светлана –участвовали в лыжных соревнованиях и заняли места с 1-гопо 4-е. На вопрос, кто какое место занял, были полученытри ответа: «Юлия заняла 1-е место, Наташа – 2-е» ;«Юлия – 2-е, Светлана – 3-е»; «Галина – 2-е, Светлана – 4-е». Отвечающие при этом признали, что одна частькаждого ответа верна, а другая – неверна. Какое место заняла каждая из учениц?
Пять мальчиков играли во дворе в футбол и разбили мячом окно.
Ваня сказал: "Это или Паша, или Денис".
Паша сказал: "Это сделал не я и не Вова".
Митя сказал: "По-моему, один из них говорит правду, а другой - нет".
А Вова сказал: "Митя, ты ошибаешься".
А бабушка сидела на лавочке и всё видела. Она сказала, что только один мальчик сказал неправду, но не выдала того, кто разбил окно.
14.14 В бюро переводов приняли на работу троих сотрудников: Диму, Сашу и Юру. Каждый из них знает ровно два иностранных языка из следующего набора: немецкий, японский, шведский, японский, китайский, французский и греческий. Известно, что
(1) Ни Дима, ни Юра не знают японского
(2) Переводчик со шведского старше переводчика с немецкого
(3) Переводчик с китайского, переводчик с французского и Саша родом из одного города
(4) Переводчик с греческого, переводчик с немецкого и Юра учились втроем в одном
институте
(5) Дима – самый молодой из всех троих, и он не знает греческого
(6) Юра знает два европейских языка
В ответе запишите первую букву имени переводчика со шведского языка и, через запятую, первую букву имени переводчика с китайского языка.
14.15Три ученика, Саша, Коля и Вова, прогуляли информатику. Когда их спросили, кому пришла в голову эта идея, они ответили следующее:
Саша: «Я никогда не призывал к прогулу, это была идея Коли».
Коля: «Я никогда не предложил бы это первым, во всем виноват Вова».
Вова: «Эта идея пришла в голову Коле. Я просто пошел за компанию».
Внутренним чутьем учитель почувствовал, что один ученик говорит правду, второй говорит правду только наполовину, а третий – лжет. Кто из учеников был инициатором прогула? Ответ дайте в виде первой буквы имени.
Полином Жегалкина
Алгебра над множеством логических функций с двумя бинарными операциями конъюнкции «&» и сложения по модулю два «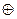 »называется алгеброй Жегалкина.
»называется алгеброй Жегалкина.
В алгебре Жегалкина, очевидно, имеют место следующие соотношения:
1. x 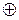 y=y
y=y 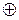 x;
x;
2. x(y 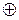 z)=xy
z)=xy 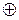 xz;
xz;
3. x 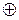 x=0;
x=0;
4. x 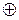 0=x;
0=x;
5. x 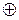 1=
1= 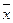 ;
;
6. x  y=xy
y=xy 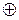 x
x 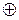 y.
y.
Если в произвольной формуле, выраженной в сигнатуре алгебры Жегалкина, раскрыть скобки и провести возможные сокращения, то получится формула, имеющая вид суммы по модулю два элементарных конъюнкций, в которых не содержатся отрицаний. Такая формула называется полиномом Жегалкина. Всякая булева функция может быть представлена в виде полинома Жегалкина:
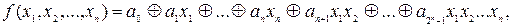
где 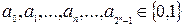 , где знак
, где знак 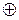 обозначает сумму по модулю два. Функция алгебры логики, для которой полином Жегалкина имеет вид:
обозначает сумму по модулю два. Функция алгебры логики, для которой полином Жегалкина имеет вид:
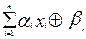
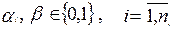 ,
,
называется линейной. Очевидно, что все функции от одной переменной линейны. Линейными являются, например, функции x 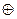 y и x
y и x 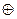 y
y 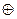 1=x~y. Для построения полинома Жегалкина можно воспользоваться следующими двумя схемами:
1=x~y. Для построения полинома Жегалкина можно воспользоваться следующими двумя схемами:
схема 1: перейти в сигнатуру алгебры Жегалкина {x&y, x 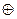 y, 1}, раскрыть скобки и провести возможные сокращения;
y, 1}, раскрыть скобки и провести возможные сокращения;
схема 2: воспользоваться приемом, который называется методом неопределенных коэффициентов, который применим лишь тогда, когда функция от n переменных задана своей таблицей истинности. Решается система линейных уравнений с 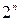 ограничениями, которые задаются через значения функции на двоичных n-мерных наборах, и
ограничениями, которые задаются через значения функции на двоичных n-мерных наборах, и 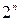 неизвестными – коэффициентами полинома Жегалкина.
неизвестными – коэффициентами полинома Жегалкина.
Алгоритм построения полинома Жегалкина:
1) построить таблицу истинности данной булевой функции; каждому единичному значению булевой функции будет соответствовать конъюнкция 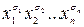 , где
, где 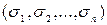 – соответствующий набор значений переменных, конъюнкции соединяются знаком «
– соответствующий набор значений переменных, конъюнкции соединяются знаком « 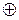 ».
».
2) заменить выражения 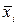 по формуле:
по формуле: 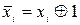 . Раскрыть скобки и привести подобные слагаемые по правилу:
. Раскрыть скобки и привести подобные слагаемые по правилу: 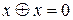 .
.
Пример 1.Построить СДНФ, СКНФ и полином Жегалкина для функции
f = (11110011).
Решение:
СДНФ имеет вид: 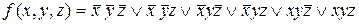 .
.
СКНФ имеет вид: 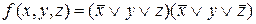 .
.
Построим полином Жегалкина:
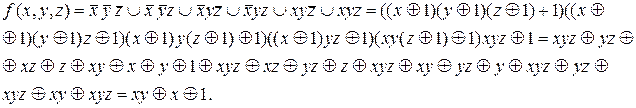 Пример 2.С помощью эквивалентных преобразований привеcти формулу f =
Пример 2.С помощью эквивалентных преобразований привеcти формулу f = 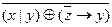 к ДНФ, КНФ, СДНФ, СКНФ, построить полином Жегалкина.
к ДНФ, КНФ, СДНФ, СКНФ, построить полином Жегалкина.
Решение:
Построим КНФ:
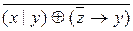 =
= 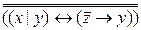 =
= 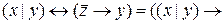
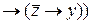
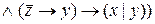 =
= 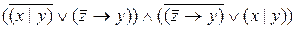 =
= 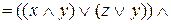
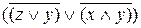 =
= 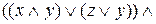
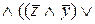
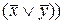
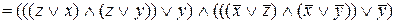 =
=
= 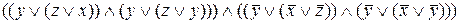 =
=
= 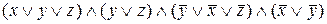 .
.
Построим СКНФ:
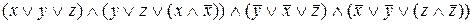 =
=
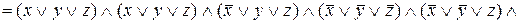
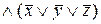 =
= 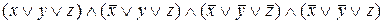 .
.
Построим ДНФ:
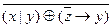 =
= 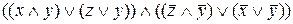 =
= 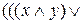
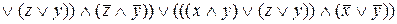 =
= 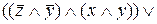
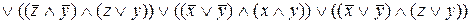 =
=
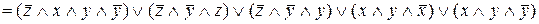
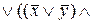
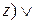
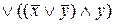 =
= 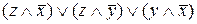 .
.
Построим СДНФ:
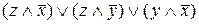 =
= 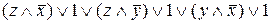 =
=
= 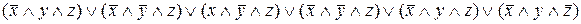
= 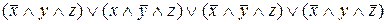 .
.
Построим полином Жегалкина:
f(x,y,z)= 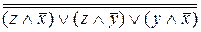 =
= 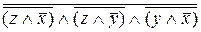 =
= 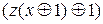
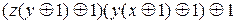
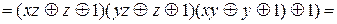
= 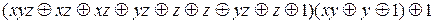
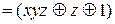
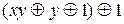 =
= 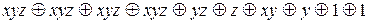 =
= 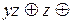
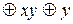 .
.
Пример 3.Найти полином Жегалкина для ДНФ 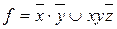 и перейти от ДНФ к КНФ, затем к СКНФ.
и перейти от ДНФ к КНФ, затем к СКНФ.
Решение:
Сначала найдем полином Жегалкина: ставим двойное отрицание и по правилам де Моргана преобразуем дизъюнкцию, потом заменяем отрицания по правилу 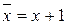 . После этого раскрываем скобки, учитывая при этом, что четное число слагаемых (по модулю два) равно нулю, а нечетное – одному такому слагаемому:
. После этого раскрываем скобки, учитывая при этом, что четное число слагаемых (по модулю два) равно нулю, а нечетное – одному такому слагаемому:
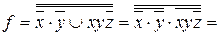 ((x+1)(y+1)+1)(xy(z+1)+1)+1 = (xy+x+y+1+1)
((x+1)(y+1)+1)(xy(z+1)+1)+1 = (xy+x+y+1+1)
(xyz+xy+1)+1=(xy+x+y)(xyz+xy+1)+1=xyz+xyz+xyz+xy+xy+xy+xy+x+y+1= xyz+x+y+1.
Здесь знак 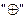 заменен на обычный знак «+» для простоты записи.
заменен на обычный знак «+» для простоты записи.
Последнее выражение и является полиномом Жегалкина.
Для того чтобы перейти к КНФ над формулой два отрицания и, оставляя временно верхнее отрицание безизменения, приводим оставшееся выражение к ДНФ. Затем по правилу де Моргана получаем КНФ. Таким образом, можем получить: 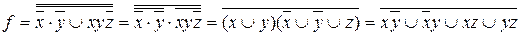 .
.
Далее по правилу Блейка можем из последнего выражения исключить yz, тогда получим: 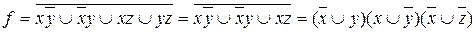 – КНФ.
– КНФ.
Чтобы из последнего выражения получить СКНФ, нужно в первой и второй дизъюнкции добавить 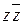 , а в третьей –
, а в третьей – 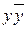 . Затем воспользуемся распределительным законом:
. Затем воспользуемся распределительным законом:
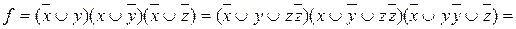
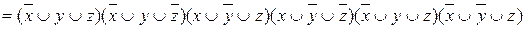 – СКНФ.
– СКНФ.
Пример 4.Для функции f(x, y, z) = (x ~ z) | ((x y) ~ (y z)) найти по таблице истинности полином Жегалкина.
Решение:
Составим таблицу истинности:
| xyz | x ~ z | x y | y z | (x y) ~ (y z) | (x~ z)|((x y) ~ (yz) |
Составим полином Жегалкина по таблице истинности. Напишем его сначала с неопределенными коэффициентами: f(x, y, z) = a0 +a1x+ a 2y+ a 3z+ a4xy+ a5xz+ a6 yz+ a7xyz.
Подставим в него по очереди все восемь наборов переменных (строк таблицы истинности) и найдем коэффициенты полинома Жегалкина.
x = 0, y = 0, z = 0: a0 = 0;
x = 0, y = 0, z = 1: a3 = 1;
x = 0, y = 1, z = 0: a2 = 0;
x = 0, y = 1, z = 1: a2 + a3+ a6 = 1, a 6 = 0;
x = 1, y = 0, z = 0: a1 = 1;
x = 1, y = 0, z = 1: a1+ a3 + a5 = 0, a5 = 0;
x = 1, y = 1,z = 0: a1+ a2 + a4 = 1, a4 = 0;
x = 1, y = 1, z = 1: a0 + a1 + a2 + a3 + a4 + a5 + a6 + a7 =0.
Так как a0 = a2 = a4 = a5 = a6 = 0, тогда a1 + a 3 + a7 = 0, откуда a7 = 0, и полином Жегалкина для данной функции имеет вид: f(x, y, z) = x+ z (для данной функции у является фиктивной переменной).
Упражнения
Определить, является ли функция линейной:
- f(x,y,z)=xyz
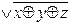 ;
; - f(x,y)=(xy
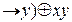 );
); - f(x,y)=(x
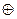 y)
y) 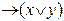 ;
; - f(x,y)=(x
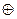 y)
y) 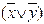 ;
; - f(x,y)=(xy
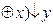 ;
; - f(x,y)=(xy
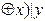 ;
; - f(x,y,z)=(xy
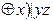 ;
; - f(x,y,z)=(xy
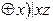 ;
; - f(x,y)=(x
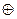 y)
y) 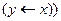 ;
; - f(x,y,z)=xyz
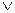
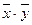 ;
; - f(x,y,z)=xyz
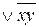 .
.
Дата добавления: 2016-04-11; просмотров: 2691;
