Индивидуальное задание. 1Определить значение высказывания, полученного из трехместного предиката на множестве X.
1Определить значение высказывания, полученного из трехместного предиката на множестве X.
1.1  x
x  y
y  z (xz = y), X = N;
z (xz = y), X = N;
1.2  z
z  x
x  y (xz = y
y (xz = y 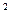 ), X = Z;
), X = Z;
1.3  z
z  y
y  x (xy > xz), X = N;
x (xy > xz), X = N;
1.4  x
x  y
y  z (xyz < yz), X = Z;
z (xyz < yz), X = Z;
1.5  x
x  z
z  y (x + y = z), X = N;
y (x + y = z), X = N;
1.6  x
x  y
y  z (xyz = yz), X = R;
z (xyz = yz), X = R;
1.7  x
x  y
y  z (xz = y), X = N;
z (xz = y), X = N;
1.8  z
z  x
x  y (x+z = y
y (x+z = y 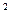 ), X = Z;
), X = Z;
1.9  z
z  y
y  x (xy > x+z), X = N;
x (xy > x+z), X = N;
1.10  x
x  y
y  z (xy-z < yz), X = Z;
z (xy-z < yz), X = Z;
1.11  x
x  z
z  y (2x + y = z), X = N;
y (2x + y = z), X = N;
1.12  x
x  y
y  z (xyz = 8), X = R;
z (xyz = 8), X = R;
1.13  x
x  y
y  z (xyz < 20), X = Z;
z (xyz < 20), X = Z;
1.14  x
x  z
z  y (x + y = z
y (x + y = z 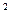 ), X = N;
), X = N;
1.15  x
x  y
y  z (xy
z (xy 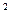 +z = y), X = R.
+z = y), X = R.
2Придумать предложения, соответствующие данным формулам, определить ее истинность, выделить свободные и связанные переменные.
2.1  x
x  y P(x, y);
y P(x, y);
2.2  x →
x →  y P(x, y);
y P(x, y);
2.3  x
x  y P(x, y) → Q(z);
y P(x, y) → Q(z);
2.4 a →  y P(x, y);
y P(x, y);
2.5  x
x  y (P(x, y) → Q(x));
y (P(x, y) → Q(x));
2.6  x P(x) →
x P(x) →  y Q( y);
y Q( y);
2.7 (  x
x  z (P(x, y) → P( y, z)));
z (P(x, y) → P( y, z)));
2.8  x
x  y P(x, y);
y P(x, y);
2.9  x →
x →  y P(x, y);
y P(x, y);
2.10  x
x  y P(x, y) →
y P(x, y) →  z Q(z);
z Q(z);
2.11  z Q(z)→
z Q(z)→  y P( y);
y P( y);
2.12  x
x  y P(x, y) →
y P(x, y) →  x Q(x);
x Q(x);
2.13  x
x  y P(x, y)
y P(x, y) 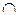
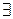 y Q(y);
y Q(y);
2.14  x P(x) →
x P(x) →  y
y  x Q( х,y);
x Q( х,y);
2.15  x
x  y P(x, y) ↔
y P(x, y) ↔  x Q(x).
x Q(x).
3Установить, какие из следующих высказываний истинны, а какие ложны, при условии, что область определения предикатов совпадает с R:
3.1 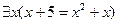 ;
;
3.2 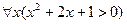 ;
;
3.3 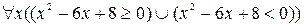 ;
;
3.4 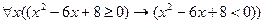 ;
;
3.5 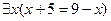 ;
;
3.6 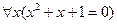 ;
;
3.7 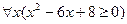 ;
;
3.8 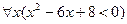 .
.
3.9 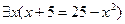 ;
;
3.10 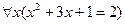 ;
;
3.11 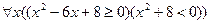 ;
;
3.12 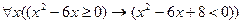 ;
;
3.13 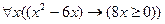 .
.
3.14 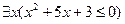 ;
;
3.15 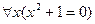 .
.
4Записать следующие логические суждения формулами логики предикатов, установить ее истинность:
4.1 Каждый знает сам себя. Значит, кого-то кто-нибудь знает.
4.2 Все учатся в каком-то учебном заведении. Значит, во всех учебных заведениях кто-то учится.
4.3 Ни одна книга не является ненужной. Учебник – книга. Значит, некоторые учебники нужны.
4.4 Имеются прилежные студенты. Ни один студент не лишен способностей. Значит, некоторые студенты, лишенные способностей, не прилежны.
4.5 Некоторые школьники и студенты – отличники, значит некоторые отличники – студенты.
4.6 Все старосты отличники и работают, значит среди работающих студентов есть отличники.
4.7 Каждый смотрит телевизор. Значит, телевизор есть у всех.
4.8 Не все студенты учатся хорошо. Значит, во всех учебных заведениях есть отличники.
4.9 Все дикие кошки имеют вертикальные зрачки. Значит, некоторые домашние кошки имеют круглые зрачки.
4.10 Существуют равнобедренные треугольники. Не все треугольники равносторонние. Значит, некоторые равнобедренные треугольники - равносторонние.
4.11 Некоторые параллелограммы - ромбы, все ромбы – четырехугольники, значит некоторые четырехугольники – не ромбы.
4.12 Все круглые предметы не имеют углов, значит все треугольные предметы не могут быть круглыми;
4.13 Все учебники – книги. Значит, все книги - учебники.
4.14 Имеются положительные числа. Ни одно отрицательное число не является натуральным. Значит, некоторые натуральные числа положительные.
4.15 Не все уравнения имеют решение, значит среди нерешенных уравнений есть решаемые.
2.2 Применение предикатов для записи предложений
С помощью предикатов можно записывать различные предложения, в том числе математические утверждения.
При этом квантор « 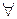 » обозначает слова – «любой», «все», «каждый», квантор «
» обозначает слова – «любой», «все», «каждый», квантор «  » обозначает слова – «существует», «некоторый», «какой-либо», сочетание «
» обозначает слова – «существует», «некоторый», «какой-либо», сочетание « 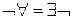 » – значит «не все», «
» – значит «не все», « 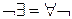 » – «никакой».
» – «никакой».
Предложение разбивается на логические части, выбираются переменные, свойства предметных переменных записываются одноместным (двухместным, трехместным) предикатом с помощью кванторов.
Пример 1.Записать предложение «Все маленькие собаки кусаются, некоторые большие кошки тоже» с помощью предикатов.
Решение:
Предметные переменные – кошки и собаки, свойства – маленькие, большие, кусаются.
Предикаты:
P(x) – x кошка,
Q(x) – x собака,
F(x) – x маленький,
L(x) – x большой,
R(x) – xкусается.
Предложение запишется в виде: 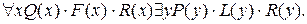
Пример 2.Записать предложение «Не всякий человек имеет друзей, так как не на всех людей можно положиться» с помощью предикатов.
Решение:
Предметная переменная – человек, свойства – друг, можно положиться.
Предикаты:
P(x) – x человек,
Q(x,у) – x друг у,
F(x) – на x можно положиться.
Предложение запишется в виде: 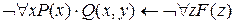 .
.
Пример 3.Записать предложение «Не все то золото, что блестит» с помощью предикатов.
Решение:
Предметная переменная – золото, свойства – блестит.
Предикаты:
P(x) – x– золото,
Q(x) – x– блестит.
Предложение запишется в виде: 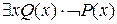 .
.
Запись 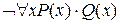 обозначает – «не все золото блестит», что является ложным.
обозначает – «не все золото блестит», что является ложным.
Пример 4. Записать предложение «Любые две непараллельные прямые пересекаются в одной точке» с помощью предикатов.
Решение:
Предметные переменные – прямая, точка, свойства – пересекается в точке.
Предикаты:
P(x) – x прямая,
Q(x) – x точка,
L(x,y,z) – x и y пересекаются в z.
Предложение запишется в виде:
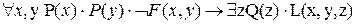 .
.
Пример 5.Записать утверждение: «числовая последовательность { 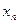 } имеет пределом число a» формулой логики предикатов и найти инверсию формулы.
} имеет пределом число a» формулой логики предикатов и найти инверсию формулы.
Решение:
Запишем данное утверждение с помощью кванторов и обозначим его A:
A =  ε
ε  N
N  n(ε >0→ (n > N →
n(ε >0→ (n > N → 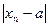 < ε )).
< ε )).
Запишем инверсию (отрицание) данного высказывания:
A =  ε
ε  N
N  n (ε >0→ (n > N →
n (ε >0→ (n > N → 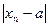 < ε ))=
< ε ))=
=  ε
ε  N
N  n (ε >0→ (n > N →
n (ε >0→ (n > N → 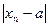 < ε ))=
< ε ))=
=  ε
ε  N
N  n (ε >0→ (n > N →
n (ε >0→ (n > N → 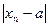 < ε ))=
< ε ))=
=  ε
ε  N
N  n (ε >0→ (n > N →
n (ε >0→ (n > N → 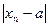 < ε )).
< ε )).
Инверсия импликации преобразуется следующим образом:
(K → M)= (K  M)= K
M)= K  M = K
M = K  M .
M .
Отсюда получаем:
A =  ε
ε  N
N  n (ε >0
n (ε >0  (n > N →
(n > N → 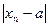 < ε)) =
< ε)) =
=  ε
ε  N
N  n (ε >0
n (ε >0  (n > N
(n > N  (
( 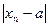 < ε))) =
< ε))) =
=  ε
ε  N
N  n (ε >0
n (ε >0  (n > N
(n > N 
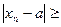 ε)) .
ε)) .
Утверждение A означает, что число a не является пределом числовой последовательности { 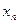 }.
}.
Многие теоремы формулируются в виде условного предложения: «Если любой элемент 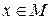 обладает свойством P(x), то он обладает свойством Q(x)»:
обладает свойством P(x), то он обладает свойством Q(x)»: 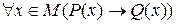 .
.
Очевидно, что если данная теорема неверна, то будет истинным утверждение: 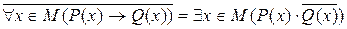 .
.
Поэтому для доказательства несправедливости теоремы нужно указать хотя бы один элемент из множества M, при котором условие P(x) истинно, а значение Q(x) ложно. Другими словами, нужно привести контрпример.
Две теоремы 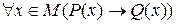 и
и 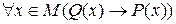 называются взаимно обратными, так как условие P(x) одной теоремы является заключением второй, а условие Q(x) второй теоремы является заключением первой. При этом одна из них называется прямой теоремой, другая – обратной.
называются взаимно обратными, так как условие P(x) одной теоремы является заключением второй, а условие Q(x) второй теоремы является заключением первой. При этом одна из них называется прямой теоремой, другая – обратной.
Теоремы 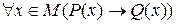 и
и 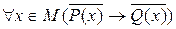 называются взаимно противоположными. В них условие P(x) и заключение Q(x) одной являются отрицанием соответствующего условия
называются взаимно противоположными. В них условие P(x) и заключение Q(x) одной являются отрицанием соответствующего условия 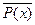 и заключения
и заключения 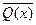 другой. Теоремы
другой. Теоремы 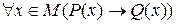 и
и 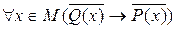 равносильны, на этом факте основывается метод доказательства от противного.
равносильны, на этом факте основывается метод доказательства от противного.
Известно, что если 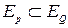 то предикат Q(x) есть следствие предиката P(x):
то предикат Q(x) есть следствие предиката P(x): 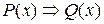 .
.
Отсюда следует, что предикат 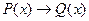 является истинным для
является истинным для 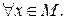 При этом предикат P(x)называют достаточным условием для Q(x), а предикат Q(x) – необходимым условием для предиката P(x).
При этом предикат P(x)называют достаточным условием для Q(x), а предикат Q(x) – необходимым условием для предиката P(x).
Если 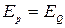 , то
, то 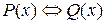 , предикаты равносильны.
, предикаты равносильны.
В этом случае взаимно обратные теоремы истинны при 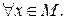 Условие P(x) является необходимым и достаточным для Q(x). Аналогично, условие Q(x) является необходимым и достаточным для P(x).
Условие P(x) является необходимым и достаточным для Q(x). Аналогично, условие Q(x) является необходимым и достаточным для P(x).
Пример 1. Записать на языке предикатов формулировку теоремы о необходимом признаке сходимости числового ряда 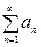 ,
, 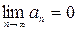 .
.
Решение:
Пусть P(x) – свойство x быть сходящимся рядом, где M = {x} – множество всех числовых рядов; Q(x) – общий член при n. Тогда формула 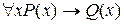 есть запись формулировки данной теоремы.
есть запись формулировки данной теоремы.
Упражнения
1. Запишите на языке логики предикатов определения:
a) Линейно упорядоченного множества (упорядоченное множество называется линейным, если для любых элементов этого множества x и y либо x = y , либо x < y , либо x > y ).
b) Ограниченной функции(функция f (x) называется ограниченной на множестве M, если существует такое неотрицательное число L, что для 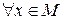 верно f (x)
верно f (x) 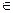 L).
L).
c) Четной функции(функция f называется четной, если область ее определения симметрична относительно начала координат и для каждого x из области определения верно f (– x) = f (x)).
d) Периодической функции (функция f называется периодической, если существует такое число T 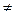 0, что при любом x из области определения f элементы x – T и x + T также принадлежат этой области, и при этом выполнено равенство f (x ± T) = f (x)).
0, что при любом x из области определения f элементы x – T и x + T также принадлежат этой области, и при этом выполнено равенство f (x ± T) = f (x)).
e) Возрастающей функции на множестве M (функция f называется возрастающей на множестве M, если для любых чисел 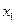 и
и 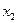 , принадлежащих множеству M, из неравенства
, принадлежащих множеству M, из неравенства 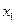 <
< 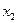 следует неравенство
следует неравенство 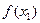 <
< 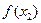 .
.
2. Пользуясь полученными в предыдущем упражнении формулами, ответьте на следующие вопросы:
1) Упорядоченное множество не является линейным?
2) Функция не является ограниченной?
3) Функция не является четной?
4) Функция не является периодической?
5) Функция не является возрастающей на множестве M ?
3. Доказать несправедливость утверждений:
a) «Если функция непрерывна в точке 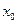 , то она и дифференцируема в этой точке»;
, то она и дифференцируема в этой точке»;
b) «Если предел n–го члена числового ряда равен нулю, то ряд сходится»;
c) «Если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником»;
d) «Если функция интегрируема на [a, b], то непрерывна на нем»;
e) «Если функция интегрируема на [a, b], то монотонна на нем»;
f) «Если числовая последовательность имеет предел, то она монотонна»;
g) «Если числовая последовательность ограничена, то она имеет предел».
4. Для каждого из следующих условий выясните, является ли оно необходимым или является ли оно достаточным для того, чтобы выполнялось неравенство 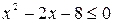 .
.
5. В следующих предложениях вместо многоточия поставьте слова «необходимо, но недостаточно», «достаточно, но не необходимо», «не необходимо и недостаточно», «необходимо и достаточно» так, чтобы получилось истинное утверждение:
1) Для того чтобы четырехугольник был прямоугольным, …, чтобы длины его диагоналей были равны.
2) Для того чтобы 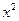 – 5x + 6 = 0 , …, чтобы x = 3.
– 5x + 6 = 0 , …, чтобы x = 3.
3) Для того чтобы сумма четного числа натуральных чисел была четным числом, …, чтобы каждое слагаемое было четным.
4) Для того чтобы функция f (x) была интегрируема на отрезке [a,b], …, чтобы f (x) была ограничена.
5) Для того чтобы окружность можно было вписать в четырехугольник, …, чтобы суммы длин его противоположных сторон были равны.
6) Для того чтобы множество A было счетным, …, чтобы его элементы можно было записать в виде нумерованной последовательности.
7) Для того чтобы числовая последовательность имела предел, …, чтобы она была ограниченной.
8) Для того чтобы числовая последовательности имела предел, …, чтобы она была монотонной и ограниченной.
6. Сформулируйте:
1) Необходимый и достаточный признак параллелограмма.
2) Необходимый, но недостаточный признак параллелограмма.
3) Достаточный, но необходимый признак параллелограмма.
4) Необходимое, но недостаточное условие того, чтобы уравнение sin x = a имело решение.
5) Достаточное, но не необходимое условие для того, чтобы уравнение
sin x = a имело решение.
6) Достаточное, но не необходимое условие для того, чтобы уравнение x 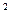 + +px+ q = 0имело вещественные корни.
+ +px+ q = 0имело вещественные корни.
Дата добавления: 2016-04-11; просмотров: 3457;
