Аналитическое задание булевых функций

Рассмотрим один вид аналитического задания булевых функций, который называется совершенной дизъюнктивной нормальной формой (СДНФ).

Пусть булева функция f ( x ) = f (x 1, x 2, …, xn) задана табл. 6.1.

Определение 6.2.Булева функция f ( x ) = f (x 1, x 2, …, xn) вида

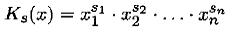
называется совершенной элементарной конъюнкцией, или конъюнктом. Здесь участвуют все переменные или их отрицания без повторений и обозначены через 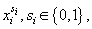переменная 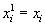или ее отрицание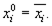

Число различных конъюнктов п переменных равно 2 n. (Почему?) Каждый конъюнкт обладает следующим важным свойством.

Теорема 6.1.Конъюнкт 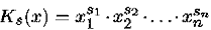равен 1 лишь на одном наборе s = ( s 1, s 2,…, sn) нулей и единиц, когда xi= si, т. е. Ks( s ) = 1.

Из этой теоремы следует, что дизъюнкция т различных конъюнктов равна 1 лишь на т наборах из нулей и единиц, соответствующих этим конъюнктам. Теперь можно сделать вывод.

Теорема 6.2.Если булева функция f ( x ) = f ( x 1, x 2, ..., xn) не является тождественно равной нулю и задана таблицей с т ≥ 1 единичными значениями, то существует единственная дизъюнкция т различных конъюнктов, соответствующих этим значениям, которая задает булеву функцию

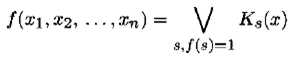
и называется совершенной дизъюнктивной нормальной формой(СДНФ) данной булевой функции.

Таблица 6.4