Полные системы булевых функций

Аналитическое задание булевых функций наводит на мысль о представлении всех булевых функций через набор некоторых выделенных основных булевых функций подобно тому, как любая элементарная функция высшей математики выражается через основные элементарные функции.

Определение 6.3.Пусть даны булевы функции f ( x 1, x 2, ..., xm); g 1( x 1, x 2, ..., xn); g 2( x 1, x 2, ..., xn); gm( x 1, x 2, ..., xn). Подставим функции giв функцию f . Получим новую булеву функцию

f ( g 1( x 1, x 2, ..., xn); g 2( x 1, x 2, ..., xn); gm( x 1, x 2, ..., xn)),

которую называют суперпозициейфункций f , g 1,…, gm. При этом такой метод получения новых булевых функций называют операцией суперпозициибулевых функций.

Определение 6.4.Набор булевых функций М = { f 1, ..., fk} называется полной системой булевых функций, или базисом, если любая булева функция выражается через них при помощи операции суперпозиции в конечном числе раз.

Пример 6.2. Набор булевых функций:

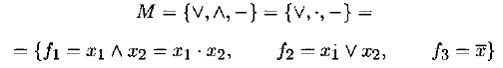
является полной системой булевых функций, так как любая булева функция может быть аналитически представлена в форме СДНФ или СКНФ. Эту полную систему называют стандартным базисом . Вот некоторые примеры разложения булевых функций в стандартном базисе:

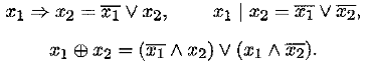
Теорема 6.3(о двух системах ). Пусть имеется полная система булевых функций М = { f 1, ..., fm}. Тогда для полноты некоторой другой системы булевых функций N = { g 1, ..., gn}необходимо и достаточно, чтобы любая функция fi∈ M выражалась через функции системы N при помощи операции суперпозиции.

Доказательство . Необходимость очевидна. (Почему?)

Достаточность . Рассмотрим произвольную булеву функцию h . Тогда она выражается через функции fi∈ M при помощи операции суперпозиции в силу полноты системы М . Но, в свою очередь, любая функция fi∈ M выражается через функции gj∈ N при помощи операции суперпозиции. Следовательно, можно через функции gjвыразить любую булеву функцию и, значит, система N — полная.

Определение 6.5.Класс булевых функций K называется замкнутым , если всякая суперпозиция функций этого класса будет функцией из этого класса.

Примеры замкнутых классов.Множество всех булевых функций F является замкнутым классом. (Почему?) Приведем пять важных замкнутых классов Поста, отличных от F :

• класс Т 0— множество булевых функций, равных 0 на нулевых значениях всех переменных;

• класс Т 1— множество булевых функций, равных 1 на единичных значениях всех переменных;

• класс S — множество самодвойственных функций, которые обладают свойством

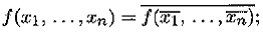
• класс L — множество линейных функций, которые в базисе Жегалкина представляются многочленом не выше первой степени;

• класс М — множество монотонных функций, которые обладают свойством

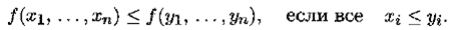
С классами Поста связан второй алгоритм определения полноты системы булевых функций, основанный на следующей теореме.

Теорема 6.4(теорема Поста — Яблонского ). Для того чтобы множество N булевых функций было полной системой, необходимо и достаточно найти для каждого из пяти замкнутых классов Поста Т 0, Т 1, S , L , M функцию из N , которая ему не принадлежит.

Пример 6.5. Рассмотрим множество из одной функции Шеффера N — {|}. Известно, что это — полная система. Проверим это вторым алгоритмом. Согласно теореме Поста, такая единственная функция должна не принадлежать ни одному из классов Поста. Так как 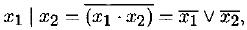то имеем 0 | 0 = 1. Следовательно, штрих Шеффера не принадлежит классу Т 0. Далее, так как 1 | 1 = 0, то штрих Шеффера не принадлежит классу Т 0. Теперь покажем, что он не самодвойственная функция:

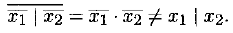
Штрих Шеффера не является линейной функцией, так как

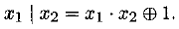
Наконец, штрих Шеффера не принадлежит классу монотонных, так как 0|0=1,1|1 = 0.

Цит. по: Дискретная математика: учебник для студ. вузов /
Т.С. Соболева, А.В. Чечкин; под ред. А.В. Чечкина. —
М.: Издательский центр «Академия», 2006. — С. 84 – 89. —
(Университетский учебник. Сер. Прикладная математика и информатика).