Определения и примеры

Часто объектом изучения в математике и ее приложениях служит множество вместе с определенной на нем структурой. Читателю уже известны поля, формирующие основу обычной арифметики, линейные пространства, обеспечивающие связь геометрических объектов с операциями над числами, множества с введенными на них бинарными отношениями. Все эти структуры образуют алгебраические системы, представляющие собой некоторые миры с определенными в них законами. Перейдем к точному определению алгебраической системы.

Рассмотрим непустое множество А . Введем понятие n -местной операции на множестве 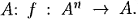Отметим, что, поскольку операция f является функцией, для любого набора (x 1, …, xn) ∈ Апрезультат применения операции f (x 1, …, xn) однозначно определен. Так как область значений операции f лежит в множестве А , то будем говорить, что операция f замкнута на множестве А .

Сигнатурой или языком ∑ называется совокупность предикатных и функциональных символов с указанием их местности. 0-местный функциональный символ называется константным символом или просто константой . Если α — функциональный или предикатный символ, то его местность обозначается через μ(α). n -местные предикатные и функциональные символы часто будем обозначать соответственно через P (n)и f (n). Если в рассматриваемой сигнатуре используются стандартные символы, такие, например, как + для операции сложения, ≤ для отношения порядка, | для отношения делимости, 0 для константного символа и другие, то мы просто пишем ∑ = {≤}, ∑ = {≤, +, ·, 0}, ∑ = { +, –, |, 0, 1} и т. д.

Алгебраической системой 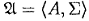сигнатуры ∑ называется непустое множество А , где каждому n -местному предикатному (функциональному) символу из ∑ поставлен в соответствие п- местный предикат (соответственно операция), определенный на множестве А . Множество А называется носителем или универсумом алгебраической системы á А , ∑ñ . Предикаты и функции, соответствующие символам из ∑, называются их интерпретациями . Обозначать интерпретации будем теми же буквами, что и соответствующие символы сигнатуры. Заметим, что интерпретацией любого константного символа является некоторый элемент (константа ) из А .

Алгебраические системы в дальнейшем будут обозначаться готическими буквами 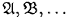(возможно, с индексами), а их носители — соответствующими латинскими буквами А , В ,... (с соответствующими индексами). Иногда мы будем отождествлять носитель с алгебраической системой.

Мощностью алгебраической системы 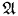называется мощность ее носителя А . В дальнейшем будем часто опускать слово «алгебраическая» и называть 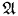системой или структурой .

Сигнатура ∑ называется функциональной , (предикатной ), если она не содержит предикатных (функциональных) символов. Система 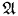называется алгеброй (моделью ), если ее сигнатура функциональна (предикатна).

Алгебра 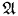сигнатуры ∑ = {f }, где μ(f )= 2, называется группоидом . Единственная здесь операция f обычно обозначается символом ·: 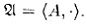Если А — конечное множество, действия операции · можно задать квадратной таблицей, в которой для каждой пары (ai, aj) ∈ А 2записан результат действия · (ai, aj). Такая таблица называется таблицей Кэли группоида 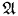. Группоид 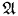называется полугруппой , если · — ассоциативная операция, т. е. для всех элементов x , y , z ∈ А верно х · (у · z ) = (х · у ) · z . Полугруппа 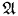называется моноидам , если существует элемент е ∈ А , называемый единицей, такой, что е · х = х · е = х для всех х ∈ А . Полугруппы и моноиды имеют особое значение в теории языков при обработке слов.

Пример 1.2. Пусть W (X ) — множество слов алфавита X . Определим на W (X ) операцию конкатенации ^ следующим образом: если α, β ∈ W (X ), то α^β = αβ, т. е результатом является слово, полученное соединением слов α и β (например. xyz ^zx = xyzzx ). Операция ^ ассоциативна, т. е. для любых слов α, β, γ верно (α^β)^γ = α^(β^γ).

Следовательно, система á W (X ), ^ñ является полугруппой. Так как для всех α ∈ W (X ) верно Λ^α = α^Λ = α, где Λ — пустое слово, то Λ удовлетворяет свойству единицы. Таким образом, система á W (X ), ^ñ является моноидом.

Моноид 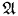= á A , ·ñ называется группой , если для любого элемента х ∈ А существует элемент х –1∈ А , называемый обратным к х , такой, что х · х –1= х –1· х = е . Группа 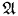называется коммутативной или абелевой , если х · y = y · х для всех x , y ∈ А .

Подсистемы

Алгебраическая система 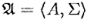называется подсистемой системы 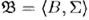(обозначается через 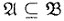), если выполняются следующие условия:

а) А ⊆ В ;

б) для любого функционального символа f n∈ ∑, соответствующих функций 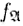и и 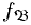любых элементов a 1, a 2, …, an∈ А выполняется равенство 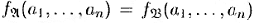, т. е. интерпретации символа f действуют одинаково па элементах из A ;

в) для любого предикатного символа P (n)∈ ∑, соответствующих предикатов 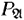и 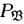справедливо равенство 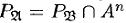, т. е. предикат 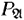содержит в точности те кортежи отношения 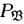, которые состоят из элементов множества А .

Если ∑ — функциональная (предикатная) сигнатура, то подсистема 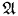алгебры (модели) 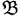называется подалгеброй (подмоделью ).

Теорема 3.1.Если 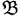— алгебраическая система , X ⊆ В , X ≠ ∅ , то существует единственная подсистема 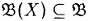с носителем , В (Х ), такая, что X ⊆ B (Х ) м 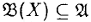для любой подсистемы 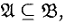для которой X ⊆ A .

Для описания устройства подсистемы 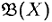определим индукцией по построению понятие терма сигнатуры ∑:

1) переменные и константные символы из ∑ суть термы;

2) f ∈ ∑ — n -местный функциональный символ, t 1, t 2, …, tn— термы, то f (t 1, t 2, …, tn) — терм;

3) никаких термов, кроме построенных по пп. 1, 2, нет.

Таким образом, термом является любое функциональное выражение, составленное с помощью сигнатурных функциональных символов.

Множество всех термов сигнатуры ∑ обозначается через Т (∑).