Топологические пространства, сходимость к точке и направленности

Определение 7.1.Пусть X — произвольное множество, τ = { Ui: i ∈ I } — некоторое семейство его подмножеств. Множество индексов I может иметь произвольную мощность. Говорят, что семейство τ задает топологиюво множестве X , если выполняются три условия:

1) все множество X и пустое множество ∅ принадлежат семейству τ;

2) объединение любого набора множеств из τ принадлежит семейству τ;

3) пересечение конечного числа множеств из τ принадлежит τ.

Множество X вместе с заданной на нем топологией τ называется топологическим пространствоми обозначается X , или подробнее ( X , τ). При этом множества из семейства τ называются открытыми множествамииз X .

Пример 7.1. Метрическая топология.Всякое метрическое пространство á Х , ρ ñ , где ρ: X × X → R +— метрика пространства, является топологическим пространством с метрической топологией . Открытыми множествами метрического пространства называются множества, которые содержат наряду с любой своей точкой x 0некоторый шар радиусом r > 0 с центром в точке x 0,

Or( x 0) = {х : ρ(х , х 0) < r }.

Пример 7.2. Тривиальная топология.Рассмотрим непустое множество X и топологию на нем τ, которая задается двумя множествами X и ∅ . Такая топология называется тривиальной .

Пример 7.3. Дискретная топология.Рассмотрим непустое множество X и зададим на нем топологию τ, которая содержит все одноточечные подмножества. Тогда любое подмножество X будет открытым множеством, т. е. τ содержит все подмножества X . Такая топология называется дискретной .

Пример 7.4. Решетчатая топология.Рассмотрим непустое множество X и разобьем его на непустые подмножества (части). Зададим топологию в X из подмножеств этого разбиения, всевозможных объединений этих подмножеств и пустого множества. Такая топология называется решетчатой . Частным случаем решетчатой топологии является тривиальная, когда разбиение состоит только из одной части X , и дискретная, когда разбиение состоит только из одноточечных подмножеств.

Определение 7.2.Пусть на одном и том же непустом множестве X заданы две топологии τ1и τ2. Если τ1⊆ τ2, то говорят, что топология τ2 мажорируеттопологию τ1. При этом если τ1≠ τ2, то говорят, что топология τ2сильнее топологии τ1или τ1слабее τ2.

Пример 7.5. Для любого непустого множества дискретная топология мажорирует любую другую топологию. В свою очередь любая топология мажорирует тривиальную топологию.

Определение 7.3.Подмножество О топологического пространства X называется окрестностьюточки x 0∈ X и пишут O ( x 0), если оно содержит некоторое открытое подмножество X , содержащее точку x 0.

Определение 7.4.Система 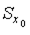окрестностей точки x 0топологического пространства X называется фундаментальной системой окрестностейэтой точки, если для каждой окрестности U этой точки существует окрестность V ∈ 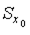, такая, что V ⊆ U .

Пример 7.6. В евклидовом пространстве Rnсовокупность открытых шаров радиусами 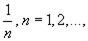содержащих точку x 0, образует фундаментальную систему окрестностей этой точки. Другую фундаментальную систему окрестностей точки x 0образуют открытые шары радиусами — 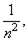содержащие эту точку.

Определение 7.5.Точка x 0топологического пространства называется предельной точкой множестваМ ⊆ X , если любая окрестность точки x 0содержит хотя бы одну точку из М , отличную от x 0.

Определение 7.6.Последовательность точек хп, п = 1, 2, ..., топологического пространства X называют сходящейся к точкеx 0∈ X и пишут 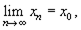если любая окрестность O ( x 0) этой точки содержит все точки последовательности, за исключением некоторого конечного их числа. Иногда говорят по-другому, что любая окрестность содержит все точки последовательности, начиная с некоторого номера.

Определение 7.7.Частично упорядоченное множество S называется направленным, если для любых двух элементов s 1, s 2∈ S существует s ∈ S , такое, что s ≥ s 1и s ≥ s 2.

Направленное множество — обобщение множества натуральных чисел, которое является частным случаем направленного множества. В свою очередь это понятие позволило американским математикам Муру и Смиту обобщить понятие последовательности, к которому переходим.

Определение 7.8.Пусть X — топологическое пространство, S — направленное множество. Тогда отображение f : S → X называется обобщенной последовательностью, или направленностью. Часто пишут xs, s ∈ S . При этом множество S называется множеством индексов направленности.

Очевидно, что любая последовательность точек из X есть направленность в X .

Пример 7.7. Рассмотрим в топологическом пространстве X точку x 0. Пусть 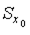— фундаментальная система окрестностей точки x 0, например все окрестности точки x 0. Выбирая по одной точке xsиз каждой окрестности s ( x 0) ∈ 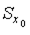, получим направленность xs, s ∈ S , в которой множество индексов S упорядочение по обратному включению, т. е. s 1≤ s 2, если s 1( x 0) ⊇ s 2( x 0).

Теперь перейдем к обобщению понятия предела последовательности.

Определение 7.9.Направленность xs, s ∈ S , в топологическом пространстве X называется сходящейся к точкеx 0∈ X , если для каждой окрестности U этой точки найдется элемент sU∈ S , такой, что при всех s ≥ sUвыполняется xs∈ U . При этом точку x 0называют пределом, направленностиxs, s ∈ S , и пишут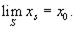

Пример 7.8. Пусть xs, s ∈ S , — направленность из предыдущего примера. Тогда она будет сходящейся к точке x 0. В самом деле, для любой окрестности U точки x 0найдется окрестность sU∈ S (из фундаментальной системы окрестностей S ), такая, что sU∈ U . Тогда для всех окрестностей s ∈ S , s ≥ sUбудет выполняться s ⊆ U и, следовательно, xs∈ U .

Пример 7.9. Всякая сходящаяся в топологическом пространстве последовательность является сходящейся направленностью в том же пространстве и к тому же пределу.