Булевы решетки подмножеств

Среди всех булевых решеток выделим класс решеток, играющих большую роль в математической информатике.

Определение 7.18.Семейство L подмножеств опорного множества X называется решеткой подмножествдля X , если выполнены условия:

1) X ∈ L ; ∅ ∈ L (эти множества играют роль единицы и нуля);

2) из λ 1, λ 2∈ L следует λ 1∩ λ 2∈ L ;

3) из λ 1, λ 2∈ L следует λ 1∪ λ 2∈ L ;

4) из λ 1, λ 2∈ L следует λ 1λ 2∈ L .

Замечание 7.3. 1. Решетка подмножеств — это булева решетка подмножеств с нулем, единицей и с операцией дополнения 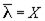λ ∈ L для любого λ ∈ L . При этом

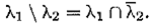
2. Отношение порядка в решетке подмножеств есть отношение включения λ 1⊆ λ 2.

При этом:

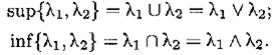
Определение 7.19.Элементы λ 1, λ 2называются дизъюнктными, если их пересечение пусто: λ 1∩ λ 2= ∅ .

Для одного множества X можно определить различные решетки подмножеств. Среди решеток имеются минимальная L 0, состоящая из двух подмножеств ∅ и X , и максимальная L *, где L *= 2 X, состоящая из всех возможных подмножеств опорного множества X .

Пример 7.20. Рассмотрим множество X всех преподавателей вуза.

Для этого множества рассмотрим три решетки подмножеств.

L 1— решетка пола;

L 2— решетка научных званий;

L 3— решетка должностей.

Атомы этих решеток:

в L 1— элементы λ 1, λ 2;

в L 2— элементы μ1, μ2, μ3;

в L 3— элементы ν 1, ν 2, ν 3, ν 4.

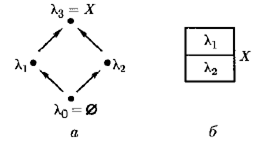
Рис. 7.5.Диаграмма Хассе решетки L 1(а ) и ее диаграмма Венна (б )

Рис. 7.6.Диаграмма Хассе решетки L 2(а ) и ее диаграмма Венна (б )

Элементы решетки изображаются диаграммами Хассе, если этих элементов небольшое число. Диаграмма Хассе решетки L 1(см. рис. 7.5, о) и диаграмма Венна (см. рис. 7.5, б ) изображены на рис. 7.5.

Для решетки L 2диаграмма Хассе будет иметь вид, показанный на рис. 7.6, а , диаграмма Венна — на рис. 7.6, б .