Конгруэнции. Фактор-алгебры. Теорема о гомоморфизме

Конгруэнцией на алгебре 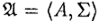называется такое отношение эквивалентности θ ∈ А 2, при котором для любого n ∈ ω, любого n -местного символа f ∈ ∑ (напомним, что сигнатура алгебры состоит только из функциональных символов), произвольных наборов (a 1, a 2, …, an), (b 1, b 2, …, bn) ∈ А n, если a 1θ b 1, a 2θ b 2, …, anθ bnто f (a 1, a 2, …, an)θ f (b 1, b 2, …, bn).

Это означает, что все операции согласованы с отношением эквивалентности θ . Например, для операции сложения это выглядит так: для любых элементов х , у ∈ А , любых а ∈ θ (х ), b ∈ θ (y ) элемент а + b принадлежит классу θ (х + у ).

Рассмотрим фактор-множество множества А по конгруэнции θ : А / θ = {θ (х ) | х ∈ А }. Определим на этом множестве алгебру сигнатуры ∑. Константе с алгебры А поставим в соответствие элемент θ (c ), который в А / θ будет интерпретировать константный символ с . Если f — n -местный символ из ∑, то зададим на множестве А / θ действие функции f по правилу

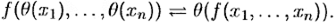
Убедимся, что для любых x 1, …, xn ∈ А это определение корректно, т. е. не зависит от выбора представителей классов эквивалентности. Действительно, 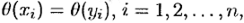то xiθ yi, откуда в силу свойства конгруэнции имеем f (x 1, …, xn)θ f (y 1, …, yn), т. е. θ (f (x 1, …, xn)) = θ (f (y 1, …, yn)).

Получившаяся алгебра 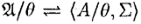называется фактор-алгеброй алгебры 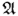по конгруэнции θ .

Очевидно, что отображение А → А / θ , при котором элементу х ∈ А ставится в соответствие класс θ (x ), является эпиморфизмом алгебры 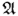на фактор-алгебру 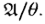Этот эпиморфизм называется естественным гомоморфизмом.

Если 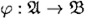— гомоморфизм алгебр, то множество Kerφ ⇌ {a , a ′ | φ (α ) = φ (α ′)} оказывается конгруэнцией на алгебре и называется ядром гомоморфизма φ .

Цит. по: Элементы дискретной математики: учебник /
С.В. Судоплатов, Е.В. Овчинникова. — М.: ИНФРА-М;
Новосибирск: НГТУ, 2003. — С. 48–57. — (Серия «Высшее образование»).