Занятие 2. Теорема Гаусса. Поле в диэлектрике

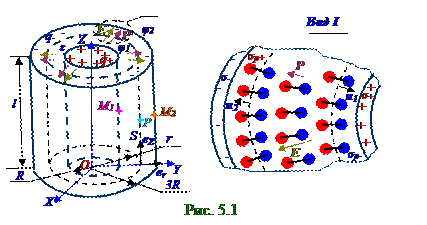
поля", P поляризованности (5.70)из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля" и D электрического смещения (5.87) из раздела 5.2 "Электростатическое поле в диэлектрике.Электрическое поле заряженных проводников. Энергия электростатического поля " представляют собой цилиндрическое векторное поле, поскольку все эти векторы(рис. 5.2.1) ориентированы перпендикулярно OZ оси, направленыс учётом q₊ положительногосвободногозарядас σ₊ поверхностнойплотностью навнутреннемцилиндре и q_- отрицательногосвободногозаряда с σ_-поверхностнойплотностьюнавнешнемцилиндре отэтой OZ оси.

Относительнаяεдиэлектрическая проницаемость диэлектрика непостоянна по всему объёму между внутренними внешнимцилиндром и зависит только от r длины(рис.2.1), т.е. модуля r радиуса-вектора, направленного по e_r орту из O начала координат основной OХY плоскости в проекцию на эту основную OХY плоскость цилиндрическойсистемы координат P точки, поэтому в этой P точке относительная εдиэлектрическая проницаемость диэлектрикаимеетследующее значение: ε = 10R²/(R² + r²), (1.1) где (рис. 05.2.1) R ≤ r ≤ 3R. Выберем l длину (рис.5.1)цилиндрического конденсатора, равную единице длины, т.е. одномуметру,тогда емкостьэтого цилиндрического конденсатораравняется C₀ погонной емкости, а q₊ погонный заряд на внутреннейобкладке цилиндрического конденсатора, заряженного до U напряжения, имеет следующий вид: q₊ = C₀U, Кл/м.(1.2)

Согласно теореме Гаусса (5.87) из раздела 5.2 "Электростатическое поле в диэлектрике.Электрическое поле заряженных проводников. Энергия электростатического поля " поток N_D вектора D электрического смещения череззамкнутую поверхность S площадью воображаемогоцилиндра l длиной и (рис. 5.1) с r радиусом, находящегося в диэлектрике между внутренними внешнимцилиндром и охватывающего свободныезаряды q₊ на внутреннемцилиндре, имеет следующий вид: ∫ DdS= q₊. (1.3) (S) Векторы D электрического смещения представляют собой цилиндрическое векторное поле инаправленыперпендикулярно боковойповерхностивоображаемогоцилиндра S = 2πrl площадью,т.е. соcтавляющая вектора D_X электрического смещения,направленнаяпо e_X орту (рис. 05.2.1) или перпендикулярнооснованиям этого воображаемогоцилиндра, равна нулю. Поэтому поверхностныйинтеграл (1.3) через боковуюповерхностьвоображаемогоцилиндра l длиной, т.е. S = 2πrl площадью имеет следующий вид: ∫ DdS=D_r2πrl = q₊l, (1.4) (S)

где D_r - проекция на направление орта e_r вектора D электрического смещения в диэлектрике.Подставляем q₊ погонный заряд (1.2) на внутреннейобкладке цилиндрического конденсатора, заряженного до U напряжения, в (1.4) и получаем следующее выражение, определяющее D_r проекциюна направление (рис. 5.1)орта e_r вектора D электрического смещения в диэлектрике между внутренними внешнимцилиндром: D_r = C₀U/2πr, Кл/м²,(1.5) где R ≤ r ≤3R; r - модуль r радиуса-вектора, направленного по e_r орту из начала O координат OХY основной плоскости в проекцию на неё P точки, в которой определяется эта D_r проекция.

Вектор D электрического смещения направлен (рис. 5.1)перпендикулярно боковойповерхностивоображаемогоцилиндра с величиной r радиуса.

Согласно (5.87) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля " E_r проекцияна направление

(рис. 5.1)орта e_r вектора E напряжённости электростатического поля в диэлектрике связана с D_r проекцией на направление e_r орта вектора D электрического смещения в диэлектрике между внутренними внешнимцилиндром следующим соотношением: E_r = D_r/ε₀ε, В/м. (1.6)Подставляем (1.5)проекцию D_r на направление (рис. 5.1)орта e_r вектора D электрического смещения в диэлектрике и (1.1) относительнуюεдиэлектрическую проницаемость диэлектрика между внутренними внешнимцилиндром в (1.6) выражение и получаем следующее выражение E_r проекциина направление e_r орта вектора E напряжённости электростатического поля в диэлектрике: E_r = C₀U(R² + r²)/20πε₀rR², В/м.(1.7) где 3R ≤ r ≤ R; r - модуль r радиуса-вектора, направленного по e_r орту из начала O координат

OХY основной плоскости в проекцию на неё P точки, в которой определяется эта E_r проекция; C₀ - погонная емкость цилиндрического конденсатора, заряженного доU напряжения.

Вектор E напряжённостиэлектростатического поля коллинеарен вектору D электрического смещения, т.к. направлен (рис.05.2.1)перпендикулярно боковойповерхностивоображаемогоцилиндра с величиной r радиуса.

Согласно (5.86)из раздела 5.2 "Электростатическое поле в диэлектрике.Электрическое поле заряженных проводников. Энергия электростатического поля " проекция P_r на направление (рис.5.1)орта e_r вектора P поляризованностидиэлектрика связанас (1.5) проекцией D_r на направление e_r орта вектора D электрического смещения в диэлектрикеи (1.7) проекцией E_r на направление e_r орта вектора E напряжённости электростатического поля в диэлектрике следующим выражением: P_r = D_r-ε₀E_r.(1.8) Подставляем (1.5) проекцию D_r на направление (рис.5.1)орта e_r вектора D электрического смещения в диэлектрике и (1.7) проекцию E_r на направление e_r орта вектора E напряжённости электростатического поля в диэлектрике в выражение (1.8) и получаем следующее выражение для проекции P_r на направление e_r орта вектора P поляризованностидиэлектрика: P_r = (C₀U/2πr){1 - [(R² + r²)/10R²]}, Кл/м². (1.9) где 3R ≤ r ≤ R; r - модуль r радиуса-вектора, направленного по e_r орту из начала O координат

OХY основной плоскости в проекцию на неё P точки, в которой определяется эта P_r проекция; C₀ - погонная емкость, цилиндрического конденсатора, заряженного доU напряжения; R - радиусвнутреннейобкладки цилиндрического конденсатора. Вектор P поляризованности диэлектрикаколлинеарен векторам D, E соответственноэлектрического смещенияи напряжённостиэлектростатического поля, т.к. направлен (рис.5.1)перпендикулярно боковойповерхностивоображаемогоцилиндра с величиной r радиуса. Согласно (5.127) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля " для нахождения φ₁ - φ₂ разности потенциаловмежду (рис. 5.1) соответственно внутренними внешнимцилиндром необходимо произвести интегрирование (1.7) проекции E_r на направление e_r орта вектора E напряжённости электростатического поля в диэлектрике по r модулю r радиуса-вектора, направленного по e_r орту из начала O координат OХY основной плоскости в проекции на неё M₁, M₂ точек.

Проекция M₁ точки, лежащей на поверхности внутреннего цилиндра, на OХY основную плоскость цилиндрическойсистемы координат удалена от начала O координатна величину r модуля

r радиуса-вектора, равного Rрадиусу этоговнутреннегоцилиндра.

Проекция точки M₂, лежащей на поверхности внешнего цилиндра, на OХY основную плоскость цилиндрическойсистемы координат удалена от начала O координатна величину r модуляr радиуса-вектора, равного 3Rрадиусуэтоговнешнего цилиндра.

Поэтому (5.127) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля " разность потенциалов φ₁ - φ₂, т.е. U напряжение между (рис. 5.1) соответственно внутренними внешнимцилиндром имеет следующий вид: 3R U = ∫ E_rdr.(1.10) R Подставляем (1.7) проекцию E_r на направление (рис.5.1)орта e_r вектора E напряжённости электростатического поля в диэлектрике, которая зависит от r длины, т.е. модуля r радиуса-вектора, направленного по e_r орту из начала O координат OХY основной плоскости в проекцию на неё P точки, в которой определяется эта E_r проекция, в (1.10) выражение. Производим интегрирование, сокращение U напряжения между внутренними внешнимцилиндром и получаем следующее выражение C₀ погоннойемкости цилиндрического конденсатора: C₀ = 20πε₀ /(4 + ln3),Ф/м.(1.11) Проекцию P_r^R на направление (рис. 5.1)орта e_r вектора P_R поляризованностидиэлектрика на границес внутренней обкладкой цилиндрического конденсатораопределим подстановкой в (1.9) модуля r = R радиуса-вектора r, направленного по e_r орту из начала O координат OХY основной плоскости в проекцию на неё M₁ точки, в которой определяется эта P_r^R проекция, вследствие чего имеет место следующее выражение: P_r^R = 8 ε₀U/R(4 + ln3), Кл/м². (1.12) Согласно (5.75) из раздела 5.2 "Электростатическое поле в диэлектрике.Электрическое поле заряженных проводников. Энергия электростатического поля" поверхностнаяплотность σ_p- поляризационныхзарядов в диэлектрике на границес внутренней обкладкой цилиндрического конденсатора, имеющей R радиус,равна P_n1,R проекциина направление (рис.2.1)внешней n₁ нормали к внутренней поверхности диэлектрика вектора P_Rполяризованности.

Согласно рис. 5.1 внешняя n₁нормаль к внутренней поверхности диэлектриканаправлена к центру цилиндрического конденсатора, а вектор P_R поляризованности диэлектрика на границес внутренней обкладкой цилиндрического конденсаторанаправлен от центраэтогоцилиндрического конденсатора, поэтому P_n1,R проекция на направление внешней n₁нормали к внутренней поверхности диэлектрика вектора P_R поляризованности отрицательна и поверхностнаяплотность σ_p- поляризационныхзарядов на границес внутренней обкладкой цилиндрического конденсатора, имеющей R радиус, согласно (5.75) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля ", с учётом (1.12) тоже отрицательнаиимеет следующий вид:

σ_p- = P_n1,R = -P_r^R = - 8 ε₀U/R(4 + ln3), Кл/м², (1.13) где P_n1,R = - P_r^R - проекция P_n1R на направление внешней n₁ нормали к внутренней поверхности диэлектрика вектора P_R поляризованности равняется(1.12) с противоположным знаком проекции P_r^R на направление (рис. 5.1)орта e_r вектора P_R поляризованностидиэлектрика на границес внутренней обкладкой цилиндрического конденсатора, поскольку e_r орт коллинеарен внешней

n₁ нормали и направлены эти векторы в противоположные стороны.

Проекцию P_r^3R на направление (рис.5.1)орта e_r вектора P_3Rполяризованностидиэлектрика на границес внешней обкладкой цилиндрического конденсатораопределим подстановкой в (1.9) модуля r = 3R радиуса-вектора r, направленного по e_r ортуиз начала O координат OХY основной плоскости в проекцию на неё M₂ точки, в которой определяется эта P_r^3R проекция, вследствие чего имеет место следующее выражение: P_r^3R = 0, Кл/м². (1.14) Согласно (5.75) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля " поверхностнаяплотность

σ_p+ поляризационныхзарядов в диэлектрике на границес внешней обкладкой цилиндрического конденсатора, имеющей 3R радиус,равна P_n2,3R проекциина направление (рис.2.1)внешней

n₂ нормали к внешней поверхности диэлектрика вектора P_3Rполяризованности.

Согласно (1.14) проекция P_r^3Rна направление (рис.5.1)орта e_r вектора P_3Rполяризованностидиэлектрика на границес внешней обкладкой цилиндрического конденсатора равна нулю, поэтому поверхностнаяплотность σ_p+ поляризационныхзарядовтоже равна нулю, вследствие чего имеет место следующее выражение: σ_p+ = P_n2,3R = P_r^3R = 0, Кл/м², (1.15)

где P_n2,3R = P_r^3R - проекция P_n2,3R на направление внешней n₂ нормали к внешней поверхности диэлектрика вектора P_3Rполяризованностиравняется(1.14) проекции P_r^3R на направление (рис.2.1)орта e_r вектора P_3Rполяризованностидиэлектрика на границес внешней обкладкой цилиндрического конденсатора, поскольку e_r орт коллинеарен внешней

n₂ нормали и направлены эти векторы в однусторону.

Объёмное(5.83) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля" распределение ρ_pплотности поляризационных зарядовс учётом определения divP дивергенциивектора P поляризованностидиэлектрика, направленного (рис.5.1) по e_r орту в цилиндрическом векторном поле, имеет следующий вид: ρ_p = - divP= - (1/r)∂(rP)/∂r. (1.16) Подставляем (1.9) проекцию P_r на направление (рис.5.1)орта e_r вектора

P поляризованностидиэлектрика, который зависит от r модуля r радиуса-вектора, направленного по

e_r орту из начала O координат OХY основной плоскости в проекцию на неё P точки, в которой определяется эта P_r проекция и получаем следующее выражение распределенияρ_pплотности поляризационных зарядов по объёму диэлектрика: ρ_p = (C₀U)/10πR², Кл/м³. (1.17) Подставляем выражение(1.11) C₀ погоннойемкости цилиндрического конденсатора в выражение (1.17) и получаем следующее окончательное выражение распределенияρ_pплотности поляризационных зарядовпо объёму диэлектрика: ρ_p = 2ε₀U/R²(4 + ln3), Кл/м³. (1.18) Согласно (1.18) распределениеρ_pплотности поляризационных зарядовпо объёму диэлектрика не зависит (рис.5.1) от r модуля r радиуса-вектора, направленного по e_r орту из начала

O координат OХY основной плоскости в проекцию на неё P точки, в которой определяется это распределение ρ_pплотности поляризационных зарядов, т.е. является постоянной и положительной величиной. Таким образом, поляризационные зарядыраспределеныравномерно по объёму диэлектрика между внутреннейи внешнейобкладкой цилиндрического конденсатора и имеют положительный знак.

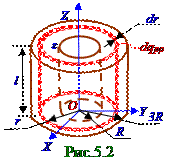
Элементарный (рис. 5.2) dq_pρположительный поляризационный заряд, находящийся в цилиндрическом слое r радиусом с dr элементарной толщиной и l длиной, с учётом выражения (1.18) распределенияρ_pплотности поляризационных зарядов по объёму диэлектрика, а также с учётом dV = 2πrldr элементарного объёма этогоцилиндрического слоя имеет следующий вид: dq_pρ = ρ_pdV = 4πε₀Urldr/R²(4 + ln3). (1.19)Полный q_pρ положительный поляризационный заряд (рис. 5.2) в объёме диэлектрика между внутреннейс R радиусом и внешнейс 3R радиусом обкладкой цилиндрического конденсатора получаем следующим интегрированием (1.19) элементарного (рис.5.2) dq_pρположительного

Полный q_pσ поляризационный заряд на поверхностях диэлектрикаскладываетсяизполяризационныхзарядов на границес внутренней обкладкой цилиндрического конденсатора, имеющей R радиус и σ_p- отрицательную поверхностную(1.13)плотностьэтих поляризационныхзарядов, а также изполяризационныхзарядов на границес внешней обкладкой цилиндрического конденсатора, имеющей3R радиус и σ_p+ положительную поверхностную(1.15)плотностьэтих поляризационныхзарядов.

Согласно (1.15)поверхностнаяσ_p+ плотность поляризационныхзарядовна границес внешней обкладкой цилиндрического конденсатора, имеющей 3R радиус, равна нулю, поэтому полный q_pσ поляризационный заряд на поверхностях диэлектрикабудет определяться толькоповерхностной(1.13) σ_p- плотностью отрицательных поляризационныхзарядов на границес внутренней обкладкой цилиндрического конденсатора, имеющей R радиус и S = 2πRl площадь, вследствие чего для этого полного q_pσ поляризационного заряда на поверхностях диэлектрика имеет место следующее выражение: q_pσ = σ_p- 2πRl, Кл.(1.21) Подставляем (1.13)в (1.21) и получаем следующее выражение для полного

q_pσполяризационного заряда на поверхностях диэлектрика, который имеет отрицательное значение вследствие того, что он определяется толькоповерхностнойσ_p-плотностью отрицательных поляризационныхзарядов на границес внутренней обкладкой цилиндрического конденсатора, имеющей R радиус: q_pσ = -16πε₀lU/(4 + ln3), Кл. (1.22) Диэлектрик(рис. 05.2.1) между внутреннейс R радиусом и внешнейс 3R радиусом обкладкой цилиндрического конденсатора до приложения между этими внутренним с Rрадиусом и внешнимс 3R радиусом цилиндрами U напряжения был электронейтрален. Согласно параграфу "Поляризация диэлектриков в электростатическом поле. Свободные заряды, связанные заряды в поляризованном диэлектрике"из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля"закону сохранения электрического заряда алгебраическая сумма электрических зарядовтел или частиц, образующих электрически изолированнуюсистему не изменяется при любых процессах, происходящих в этой системе, вследствие чего после приложения между внутреннейс R радиусом и внешнейс 3R радиусом обкладкой цилиндрического конденсатора U напряжения диэлектрик должен остаться электронейтральным. Это означает равенство нулюq_∑ суммарного заряда после приложения между внутреннейс R радиусом и внешнейс 3R радиусом обкладкой цилиндрического конденсатора U напряжения, т.е. равенство нулю суммыполного (1.20) q_pρполяризационного заряда в объёме диэлектрикас полным (1.22) q_pσ поляризационным зарядом на поверхностях диэлектрика, т.е. выполнения следующего равенства: q_∑ = q_pρ + q_pσ = 0. (1.23) Выполнение (1.23) равенства свидетельствует о правильностирасчёта.

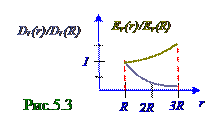
находящейся на внутреннейс R радиусом обкладке цилиндрического конденсатора с использованием (1.5) имеет следующий вид: D_r(r)/D_r(R) = R/r, (1.24)

где 3R ≤ r ≤ R.

Максимальное(рис.5.2.3) D_rmaxзначение проекция D_r(r) на направление (рис.5.2.1)орта e_r вектора D электрического смещения принимает в точках диэлектрика, находящихся на внутреннейс

R радиусом обкладке цилиндрического конденсатораи имеющее (1.5), (1.11) следующее значение: D_rmax= C₀U/2πR = 20πε₀U/(4 + ln3)2πR =10ε₀U/(4 + ln3)R. (1.25) Отношение проекции E_r(r) на направление (рис. 05.2.3)орта e_r вектора E напряжённости электростатического поля в произвольной точке диэлектрика, находящейся (рис.2.1) на r расстояниимежду внутреннейс R радиусом и внешнейс 3R радиусом обкладкой цилиндрического конденсатора, к проекции E_r(R) на направление e_r орта вектора E_R напряжённости электростатического поля в точке диэлектрика, находящейся на внутреннейс R радиусом обкладке цилиндрического конденсатора с использованием (1.7) имеет следующий вид: E_r(r)/ E_r(R) = (R² + r²)/2rR, (1.26) где 3R ≤ r ≤ R.

Максимальное(рис.5.2.3) E_rmaxзначение проекции E_r(R) на направление (рис.5.2.1)орта e_r вектора E напряжённости электростатического поляпринимает в точках диэлектрика, находящихся на внешнемс 3R радиусом обкладке цилиндрического конденсатора и имеющее (1.7), (1.11) следующее значение:

E_rmax = C₀U(R² + 9R²)/20πε₀3RR² = 20πε₀U10R²/(4 + ln3)20πε₀3R³ =10U/(4 + ln3)3R.(1.27)

Задача 1

Внутри шара R = 3, 00 см радиусом из однородного изотропного диэлектрика с

ε = 5, 00 относительной диэлектрической проницаемостью создано однородноеэлектрическое поле с модулем E = 100 В/м вектора E напряжённости этого электрического поля.Найти максимальную

σ_pmax поверхностнуюплотностьполяризационныхзарядов этого шара и его полный

q_p поляризационныйзаряд одного знака. Дано: R; ε; E / σ_pmax = ? q_p = ?

Согласно (5.70)из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля"у изотропногодиэлектрика χ = ε - 1 относительная диэлектрическая χвосприимчивостьвещества величина скалярнаяи вектор

P поляризованностисовпадает по направлению свектором E напряжённостиэлектрическогополя в этом диэлектрике, вследствие чего имеет место следующее выражение: P = ε₀χE = ε₀(ε - 1)E,(2.1)где χ = (ε - 1) - где χ относительная диэлектрическаявосприимчивостьвещества связана согласно (5.87) из раздела 5.2 "Электростатическое поле в диэлектрике.Электрическое поле заряженных проводников. Энергия электростатического поля"cε относительной диэлектрическойпроницаемостью этого вещества.

Согласно (5.75) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля " σ_p поверхностнаяплотностьполяризационныхзарядовравна следующей P_n проекциина внешнюю nнормаль к поверхности диэлектрикавектора P поляризованностив этом диэлектрике:

σ_p = P_n = Pcos(P^n)=ε₀(ε - 1)Ecos(E ^n),(2.2)

где (P^n) =(E ^n) - угол между вектором P поляризованностиили согласно (2.1)между вектором

E электрическогополя и внешней nнормалью к поверхности диэлектрика;

P=ε₀(ε - 1)E - модуль вектора P поляризованностидиэлектрика.

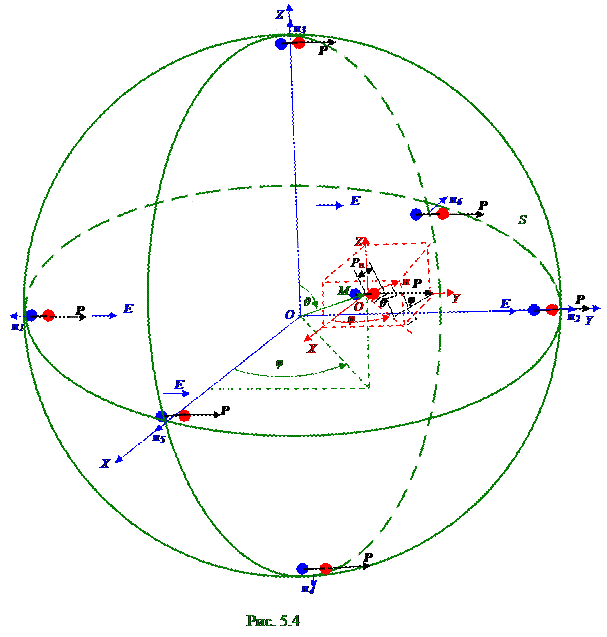
Согласно условию задачи вектор E напряжённостиэлектрическогополя в шаре (рис.5.4), изготовленного из однородного изотропного диэлектрика, совпадает по направлению свнешней nнормалью к поверхности этого диэлектрикав OХY плоскости на OY оси, поэтому (2.1) вектор

P поляризованности диэлектрикана правомполушарии коллинеарени направлен в одну сторону свектором внешней n₂нормали, а на левомполушарии коллинеарени направлен в противоположную сторону свектором внешней n₁нормали.

На правом(рис.5.4) полушарии в OХY плоскости на OY оси(P^n) угол между вектором P поляризованностиивнешней n₂нормалью численно равен 0°, поэтому (2.2) P_n проекцияна внешнюю n₂нормаль к поверхности диэлектрикавектора P поляризованностив этом диэлектрике положительна,максимальна и равна P модулю вектора P поляризованностидиэлектрика.

Вследствие этого (2.2) σ_pmax поверхностнаяплотностьполяризационныхзарядов (рис. 5.4) на поверхностиправогополушария в OХY плоскости на OY осиположительна,максимальнаи имеет следующее значение: σ_pmax = ε₀(ε - 1)E. (2.3) На левом(рис. 5.4) полушарии в OХY плоскости на OY оси(P^n) угол между вектором P поляризованностиивнешней n₁нормалью численно равен 180°, поэтому (2.2) P_n проекцияна внешнюю n₁нормаль к поверхности диэлектрикавектора P поляризованностив этом диэлектрике отрицательна,максимальна по модулю и равна P модулю вектора P поляризованностидиэлектрика с отрицательнымзнаком.

Вследствие этого (2.2) σ_pmax поверхностнаяплотностьполяризационныхзарядов (рис.5.4) на поверхностилевогополушария шара в OХY плоскости на OY осиотрицательна,максимальнапо модулю и имеет следующее значение: σ_pmax = - ε₀(ε - 1)E. (2.4)

В верхнейи нижней(рис. 5.4), а также переднейи задней точках сферической поверхности соответственно по OZ, OX оси (P^n) угол между векторами P поляризованностиивнешними n₃,n₄, n₅,n₆ нормалями численно равен 90°, поэтому (2.2) P_n проекциина эти внешние n₃,n₄, n₅,n₆ нормали к поверхности диэлектрикавектора P поляризованностив диэлектрикеравны нулю.

Вследствие этого (2.2) σ_p поверхностнаяплотностьполяризационныхзарядов (рис. 5.4) в верхнейи нижней(рис. 5.4) точках сферической поверхности по OZ оси равна нулю.

На правом(рис. 5.4) полушарии внешние n нормали ксферической поверхности направлены в одну сторону с вектором P поляризованности диэлектрика, поэтому (2.2) P_n проекциина внешнюю nнормаль к поверхности диэлектрикавектора P поляризованностив этом правомполушарииположительны.

Вследствие этого (2.2) σ_p поверхностнаяплотностьполяризационныхзарядов (рис. 5.4) на поверхностиправогополушария положительна, а полный q_p положительный поляризационныйзаряд на поверхностиправогополушария равен по величине и противоположен по знаку полному

q_p отрицательному поляризационномузаряду на поверхностилевогополушария.

Вектор P поляризованности(рис. 5.4) в произвольнойM точке на поверхностиправогополушария направлен по OY оси, авнешняя n нормаль в этой M точке сферической поверхности диэлектрика направлена в ту же сторону, что ивектор P поляризованности, но под некоторым углом, меньшим 90°. Поэтому (2.2) P_n проекцияна внешнюю nнормаль к поверхности диэлектрикавектора

P поляризованностина поверхностиправогополушария положительна, равнаположительной

σ_pM поверхностнойплотностиполяризационныхзарядов (рис.5.2.4) впроизвольнойM точке этого правогополушария и имеет следующий вид: σ_pM =P_n= Psinφsinθ = ε₀(ε - 1)Esinφsinθ, (2.5)

где φ, θ -соответственноугол долготы и полярный угол всферической системе координат, под которыми направлен радиус - векторвпроизвольнуюM точку на поверхностиправогополушария диэлектрика.

Элементарный положительныйdq_p заряд на элементарной поверхности dS площадью, находящийся (рис. 5.4) в окрестности произвольнойM точки правогополушариядиэлектрикас учётом (2.5) σ_pM поверхностнойплотностиполяризационныхзарядов в этой произвольнойM точке имеет следующий вид: dq_p = σ_pM dS = ε₀(ε - 1)EsinφsinθR²sinθdθdφ = ε₀(ε - 1)ER²sinφsin²θdφdθ, (2.6)

где dS = R²sinθdθdφ - площадь dS элементарной поверхности (9.95) из раздела 9.0 "Электромагнитные волны. Излучение" в сферической системе координат в окрестности произвольнойM точки правогополушариядиэлектрика, имеющей полярный θ уголи φ угол долготы и находящейся от

O начала координат на R расстоянии.

Полный q_p положительный поляризационныйзаряд на (рис.5.4) поверхностиправогополушария S площадью равен следующему кратному интегралу от всех элементарных положительных

dq_p зарядов на элементарных поверхностях dS площадью:

π π

q_p = ∫dq_p = ε₀(ε - 1)ER²∫sinφdφ∫sin²θdθ = ε₀(ε - 1)ER²2(π/2) = πε₀(ε - 1)ER², (2.7)

S 0 0

где φ, θ -соответственноугол долготы и полярный угол изменяется в пределах от 0 до π.

Задача 2