Занятие 1. Электростатическое поле в вакууме. Принцип суперпозиции. Проводники в электростатическом поле
Задача 1
|
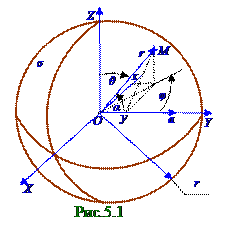
направленным (рис. 05.1) по OY оси, и rрадиусом - вектором произвольной M точки заряженной сферы относительно её O центра.
Радиус - вектор r произвольной M точки сферы относительно её O центра имеет проекции на OX, OY оси, имеющих (рис. 5.1) x, y координаты соответственно, поэтому связь α угла наклона этого r радиуса - вектора произвольной M точки сферы относительно OX оси с φ, θ углами соответственно долготыи полярногов сферической системе координат имеет следующий вид: cosα = y/r = (x2 + y2)1/2cos φ/[(x2 + y2)1/2/sinθ] ↔ cosα = cosφsinθ. (1.2)
Подставляем (1.2) в (1.1) и получаем следующее выражение σ поверхностной плотности
(рис. 05.1.2) заряженной сферы r радиуса в зависимости от aмодуля aпостоянного вектора и φ, θ углов соответственно долготы, полярного rрадиуса - вектора произвольной M точки сферыв сферической системе координат: σ = arcosφsinθ.(1.3)
|
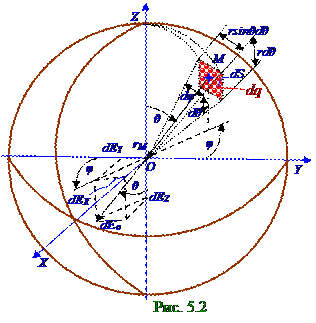
Малый положительный заряд (1.5) dq можно считать точечным электрическимзарядом, поэтому выражение модуля dEOвектора dEOнапряженности электростатическогополя в вакууме, создаваемого в O центре заряженной сферы этим малым положительным dq зарядом, с учётом (5.12) из раздела 5.1 " Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля.Работа и потенциал электростатического поля"имеет следующий вид: dEO=(1/4πε0)(dq/rM2) = (1/4πε0)arMsin2θcosφdθdφ = (1/4πε0)arsin2θcosφdθdφ, (1.6)где rM - модуль (рис. 05.1.2) вектора rM, направленный от малого положительного dq заряда, сосредоточенного в произвольной M точке сферы на (1.4) элементарной поверхности dS площадью, в
O центре заряженной сферы, где вычисляется результирующий вектор EO напряженности электростатическогополя в вакууме; rM = r, т.е. модуль (рис.1.2) вектора rM, направленный от малого положительного dq заряда в O центр заряженной сферы, равенr радиусу заряженной сферы.
Проекции (рис.5.1.2) dEx, dEy и dEz вектора dEOнапряженности электростатическогополя в вакууме, создаваемого в O центре заряженной сферы малым (1.5) положительным dq зарядом, с учётом (1.6) имеет следующий вид: dEY= - dEsinθcosφ = - (ar/4πε0)sin3θcos2φdθdφ; (1.7)
dEZ = - dEcosθ = - (ar/4πε0)sin2θcosθcosφdθdφ; (1.8)
dEX = dEsinθsinφ = (ar/4πε0)sin3θsinφdθdφ, (1.9)
где знак "-" в (1.7) и (1.8) поставлен потому, что вектор dEMнапряженности электростатическогополя в вакууме, создаваемого в O центре заряженной сферы малым (5.30) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля"положительным dq зарядом, направлен по OY и OZ осям в отрицательную сторону.
Проекции (рис. 05.1.2) Ex, Ey и Ez вектораEO напряженности электростатическогополя в вакууме, создаваемого в O центре заряженной сферы всеми малыми (1.5) положительными dq зарядами, с учётом (1.7), (1.8) и (1.9) определяются интегрированиемпо сферической поверхностиr радиусом и имеют следующий вид: π 2π
EX= - (ar/4πε0)∫sin3θdθ∫cos2φdφ = - ar/3ε0; (1.10)
0 0
π 2π
EY= - (ar/4πε0)∫ sin2θcosθdθ∫cosφdφ = 0; (1.11)
0 0
π 2π
EZ= (ar/4πε0)∫ sin3θdθ∫sinφdφ = 0. (1.12)
0 0
Согласно (1.10), (1.11) и (1.12) при (рис. 05.1.2) направлении постоянного a вектора вдоль положительного направлении OY оси векторEO напряженности электростатическогополя в вакууме, создаваемого в O центре заряженной сферы всеми малыми (5.30) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля" положительными dq зарядами на сферической поверхностиr радиусом, направлен в отрицательную сторону OY оси, т.е. этот вектор
EO напряжённости электростатическогополя в вакууме противонаправлен постоянному a вектору.
Поэтому в векторном виде векторEO напряженности электростатическогополя в вакууме, создаваемого в O центре заряженной сферы всеми малыми положительными dq зарядами на сферической поверхностиr радиусом, коллинеарен, направлен в противоположную сторону aпостоянному вектору и имеет следующий вид: E = - ar/3ε0. (1.13)
Задача 2
Бесконечно длинная круглая цилиндрическаяповерхность заряжена равномерно в вакууме по длине с поверхностной плотностью σ = σ0 cosφ, где φ - полярный угол цилиндрическойсистемы координат, т.е. угол долготы; σ0 - положительное число, имеющее размерность [Кл/м2] поверхностной плотности заряда. Ось OZцилиндрическойсистемы координат совпадает с осью данной круглой цилиндрическойповерхности. Найти модуль E и направление вектора E напряжённости электростатическогополя на оси OZцилиндрическойсистемы координат.
Дано: σ = σ0 cosφ /E = ?E = ?
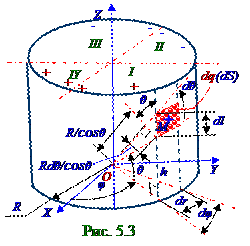
Заряд dq, сосредоточенный (рис. 5.3) в произвольной M точке цилиндрическойповерхности на элементарной поверхности dS площадью с σ = σ0 cosφ поверхностнойплотностью зарядов(5.9)из раздела 5.1."Электростатика", имеет следующий вид: dq = σdS = σ0 cosφdrdl, (2.1)
где согласно знаку cosφ функции dq заряд положителен в I -, IY - ой и отрицателен в II - и III - ой четвертях OXY координатной плоскости.
Длина dl элементарной поверхности dS площадью (рис. 05.1.3) имеет следующее значение: dl=Rdθ/cos2θ, (2.2)
где R/cosθ - длина гипотенузы в прямоугольном треугольнике, у которого один катет образован R радиусомкруглой цилиндрическойповерхности, а вторым катетомявляется h высота, на которой находится цилиндрическойповерхности, а вторым катетомявляется h высота, на которой находится элементарная поверхность dS площадью относительно OXY координатной плоскости; Rdθ/cosθ - длина катета в прямоугольном треугольнике, расположенном напротив малогоdθ угла, а второй катет вследствие малостиэтого dθ угла имеет R/cosθ величину, равную гипотенузе; Rdθ/cos2θ - длина гипотенузы в прямоугольном треугольнике, имеющем Rdθ/cosθ длину катета, прилежащего θ углу.
|
круглой цилиндрическойповерхности I -ой четверти OXY координатной плоскости, имеет симметрично расположенный относительно 0 начала координат отрицательный dq' заряд в M' точке круглой цилиндрическойповерхности в III -ей четверти OXY координатной плоскости, равный по модулю положительному dq' заряду.
Линия (рис.5.3 а), соединяющая M' точку с M' точкой, делится пополам 0 началом координат и r расстояние от элементарной поверхности dS площадью в этих точках от 0 начала координат имеет следующее значение: r = R/cosθ,(2.5)
где θ - угол между линией, соединяющей M' и M' точки, и OXY координатной плоскостью, относительно которой элементарные поверхности dS площадью в M' и M' точках расположены симметрично.
Положительный dq' заряд, сосредоточенный (рис. 5.1.3 а) на элементарной поверхности
dS площадью в произвольной M' точке круглой цилиндрическойповерхности I -ой четверти
OXY координатной плоскости, и симметрично расположенный относительно 0 начала координат отрицательный dq' заряд в M' точке круглой цилиндрическойповерхности в III -ей четверти OXY координатной плоскости находятся на линии, соединяющей M' и M' точки. Эти dq' и dq' заряды отстоят от 0 начала координат на (2.5) одинаковомr = R/cosθ расстоянии, они противоположны по знаку и равны по модулю, поэтому в точке 0 начала координат имеют как точечные зарядывекторы dE'/2 напряженности электростатическогополя в вакууме, одинаковонаправленные и имеющие dE'/2 модули следующего значения: dE'/2 = (1/4πε0)(dq'/r2),(2.6)
где dq' = dq' = | dq' | - модуль положительного dq' заряда, сосредоточенного (рис.5.3 а) на элементарной поверхности dS площадью в произвольной M' точке круглой цилиндрическойповерхности I -ой четверти OXY координатной плоскости, и симметрично расположенный относительно 0 начала координат отрицательного dq' заряд в M' точке круглой цилиндрическойповерхности в III -ей четверти OXY координатной плоскости.
Подставляем (2.5) r расстояние (рис.5.3 а) от элементарной поверхности dS площадью с положительным dq' и отрицательным dq' зарядами до 0 начала координат, а также подставляем (2.4) значение dq' модуля зарядов, сосредоточенных в произвольной M' точке исимметрично расположенный M' точкекруглой цилиндрическойповерхности на элементарной поверхности
dS площадью, вследствие чего получаем следующее выражение dE'/2 модуля вектора
dE'/2 напряженности электростатическогополя в вакууме от положительного dq' или отрицательного dq' заряда в точке 0 начала координат:
dE'/2 = (1/4πε0)[(σ0cosφ'R2/cos2θ)dφdθ]/(R/cosθ) 2 =(1/4πε0)(σ0cosφ'dφdθ) ↔
↔ dE' = (1/2πε0)(σ0 cosφ'dφdθ),(2.7)
где dE' - модуль (рис.5.3 а) суммарного вектора dE' напряженности электростатическогополя в вакууме от положительного dq' и отрицательного dq' заряда в точке 0 начала координат; φ' - полярный угол цилиндрическойсистемы координат, т.е. угол долготы. Этот φ' полярный угол (рис.5.3 а) отсчитывается от OX оси до линиипересечения плоскости, в которой находятся dq' и dq' заряды.
Парасимметрично расположенных относительно OYZ координатной плоскости (рис.5.3 а) зарядам dq' и dq' (рис.5.3 б) отрицательного dq'' заряда в M'' точке круглой цилиндрической
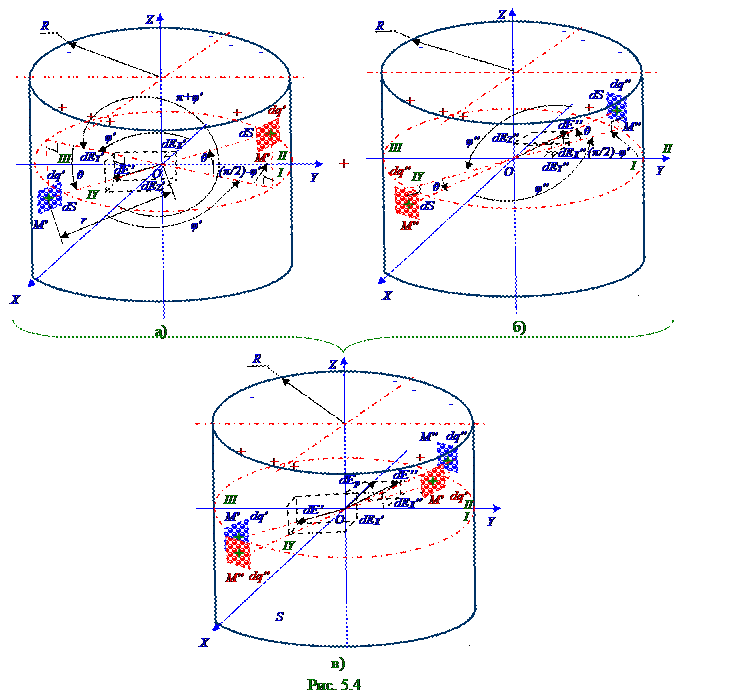
поверхности во II -ой четверти OXY координатной плоскости и положительного dq'' заряда в M'' точке круглой цилиндрическойповерхности в IY - ой четверти OXY координатной плоскости создаёт от этих отрицательного dq'' и положительного dq'' зарядов в точке 0 начала координатсуммарныйвектор dE'' напряженности электростатическогополя в вакууме, имеющий модуль dE'', равный модулю dE',а этот вектор dE'' противоположно направлен вектору dE'напряженности электростатическогополя в вакууме (рис.5.3 а) от зарядов dq' и dq'.
Заряды(рис.5.3 а) dq' и dq', сосредоточенные на элементарной поверхности dS площадью соответственно в произвольной M' точке круглой цилиндрическойповерхности I -ой четверти
OXY координатной плоскости и симметрично расположенной относительно 0 начала координат
M' точке в III -ей четверти этой OXY координатной плоскости находятся в плоскости, перпендикулярной OXY координатной плоскости. Пересечение этой плоскости с OXY координатной плоскостью образует (рис.5.3 а) линию, составляющую φ' угол с OX осью, а эта линия составляет с
OY осью (π/2)-φ' угол.
Парасимметрично расположенных относительно OYZ координатной плоскости (рис. 5.3 а) зарядам dq' и dq' (рис. 5.3 б) отрицательного dq'' заряда в M'' точке круглой цилиндрическойповерхности во II -ой четверти OXY координатной плоскости и положительного dq'' заряда в M'' точке круглой цилиндрическойповерхности в IY - ой четверти этой OXY координатной плоскости находятся в плоскости, перпендикулярной OXY координатной плоскости. Пересечение этой плоскости с OXY координатной плоскостью образует (рис.5.3 б) линию, составляющую φ'' угол с OX осью, а эта линия составляет с OY осью (π/2)-φ' угол, поскольку отрицательный dq'' заряд в M'' точке круглой цилиндрическойповерхности во II -ой четверти OXY координатной плоскости и положительный dq'' заряда в M'' точкекруглой цилиндрическойповерхности в IY - ой четверти
OXY координатной плоскости находятся в плоскости, симметричной относительно OYZ координатной плоскости. Поэтому φ'' угол (рис.5.3 б) имеет следующее значение:
φ'' = (π/2) + (π/2)-φ' = π - φ'.(2.8)
Величина (рис.5.3 а, б) dEX', dEX'' проекций на OX осьс учётом равного (2.7)
dE/2 = dE'/2 = dE''модуля векторов dE'/2, dE''напряжённости электростатическогополя в вакууме от положительных dq', dq'' и отрицательных dq', dq'' зарядов в точке 0 начала координат имеет с учётом (2.8) следующий вид: dEX' = dE/2cos(π + φ')cosθ = - (1/4πε0)(σ0cos2φ'cosθdφdθ); (2.9)
dEX'' = dE/2cos φ''cosθ = dE/2cos(π - φ')cosθ = - (1/4πε0)(σ0cos2φ'cosθdφdθ), (2.10)
где (π + φ') - полярный угол цилиндрическойсистемы координат, т.е. угол долготы; этот φ' полярный угол (рис. 5.3 а) отсчитывается от OX оси до линиипересечения плоскости, в которой находитсявектор dE'/2 напряжённости электростатическогополя в вакууме от положительного dq' и отрицательного dq' зарядов в точке 0 начала координат
Проекции (рис.5.3 в) на OY, OZ оси dE', dE'' векторов напряженности электростатическогополя в вакууме от положительных dq', dq'' и отрицательных dq', dq'' зарядов в точке 0 начала координат равны по величине и имеют противоположныезнаки, поэтому результирующийdEр вектор напряженности электростатическогополя в вакууме от положительных dq', dq'' и отрицательных dq', dq'' зарядов в точке 0 начала координат имеет dEрX проекцию только на OX ось и направлен в сторону, противоположную этой OX оси, о чём свидетельствует "-"отрицательный знак в (2.9), (2.10) выражениях dEX', dEX'' проекций на OX осьвекторов dE'/2, dE''напряжённости электростатическогополя в вакууме от положительных dq', dq'' и отрицательных dq', dq'' зарядов в точке 0 начала координат.
Величина (рис.5.3 в) dEрX проекции на OX осьрезультирующегоdEр вектора напряженности электростатическогополя в вакууме от положительных dq', dq'' и отрицательных dq', dq'' зарядов в точке 0 начала координат имеет с учётом (2.9), (2.10) следующий вид:
dEрX = dEX' + dEX'' = - (1/2πε0)(σ0cos2φ'cosθdφdθ). (2.11) Величина (рис.5.3 в) EрX проекции на OX осьрезультирующегоdEр вектора напряженности электростатическогополя в вакууме от всех положительных dq', dq'' и отрицательных dq', dq'' зарядов в точке 0 начала координат имеет с учётом (2.11) следующий вид: π/2 π
EрX = ∫dEрX = - (σ0/2πε0)∫cosθdθ ∫cos2φ'dφ = - σ0 /2ε0 ,(2.12)
S -π/2 0
где S - площадь круглой цилиндрическойповерхности, заряженной равномерно в вакууме по длине с поверхностной плотностью σ = σ0 cosφ; "- π/2" - "π/2" - пределы (рис.5.3 в) интегрирования по
θ углу; "0" - "π"-пределы интегрирования по φ' полярному углу цилиндрическойсистемы координат, которые включают только I -ую и II -ую четверти OXY координатной плоскости, т.е. толькоправуючасть круглой цилиндрическойповерхности, поскольку в (2.12) подинтегральной функцией является
dEрX проекции на OX осьрезультирующегоdEр вектора напряженности электростатическогополя в вакууме от парположительных dq' и отрицательных dq' зарядов, а также от пар симметрично расположенных относительно OYZ координатной плоскости зарядам dq' и dq' отрицательного dq'' и положительного dq'' зарядов.
Результирующий Eр вектор напряженности электростатическогополя в вакууме от всех положительных dq', dq'' и отрицательных dq', dq'' зарядов, расположенныхв вакууме на круглой цилиндрическойповерхности равномерно по длине с поверхностной плотностью
σ = σ0 cosφ, в произвольной точке осиэтойкруглой цилиндрическойповерхности согласно (2.12) имеет проекцию только по OX оси и направлен этот результирующий Eр вектор напряженности электростатическогополя в вакууме противоположно OX оси.
Задача 3
|
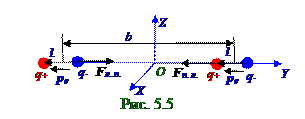
момента, которые направлены противоположно OY оси.
|
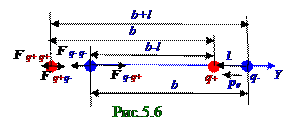
"Электростатика" следующий вид: Fq-q+ = q2/4πε0(b-l)2, (3.1) где F q-q+ - проекция (рис. 5.1.6) на OY ось вектораF q-q+ силы, действующего на отрицательный
q- заряд левого диполя со стороны положительного q+ заряда правого диполя; (b-l) - расстояние между этими зарядами; q+ = | q- | = q - модуль суммарногоположительного q+ или отрицательного
q- зарядов; ε0 = 8,85·10-12 Ф/м - электрическая постоянная; Fq- q-= - q2/4πε0b2, (3.2) где F q- q- - проекция (рис.5.6) на OY ось вектораF q- q- силы, действующего на отрицательный
q- заряд левого диполя со стороны отрицательногоq- заряда правого диполя; b - расстояние между этими зарядами; знак "-" в (3.2) потому, что векторF q- q- силынаправлен по OY оси в отрицательную сторону; Fq+q-= q2/4πε0(b+l)2, (3.3) где Fq+q- - проекция (рис. 5.1.6) на OY ось вектораFq+q- силы, действующего на положительный
q+ заряд левого диполя со стороны отрицательногоq- заряда правого диполя; (b+l) - расстояние между этими зарядами; F q+ q+ = - q2/4πε0b2, (3.4) где F q+ q+ - проекция (рис. 5.1.6) на OY ось вектораFq+ q+ силы, действующего на положительный
q+ заряд левого диполя со стороны положительного q+ заряда правого диполя; b - расстояние между этими зарядами; знак "-" в (3.4) потому, что векторFq+ q+силынаправлен по OY оси в отрицательную сторону.
Проекция (рис. 5.5)Fл..п. на OY ось вектораFл.п..силы, действующего на левый диполь со стороны правого диполя, равна сумме (3.1), (3.2), (3.3) и (3.4) и имеет следующий вид:
Fл..п. = Fq-q+ + Fq- q-+ Fq+q- + F q+ q+ = [q2/4πε0(b-l)2] - [q2/4πε0b2]+ [q2/4πε0(b+l)2] - [q2/4πε0b2] =
= q2l2(3b2 - l2)/2πε0b6 ≈ 3pe 2/2πε0b4, (3.5) гдеpe = ql - модульвектора pe дипольногоэлектрического момента (5.61) из раздела 5.1." "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля"; согласно
b >> l условию.
Знак "+" в (3.5) свидетельствует о том, что векторFл.п..силы, действующего на левый диполь со стороны правого диполя, направлен по OY оси в положительную сторону, т.е. левый диполь притягивается к правому диполю.
Согласно третьему закону Ньютона (1.49) из раздела 1.0. "Физические основы механики"в механической системе двух одинаковыхэлектрических диполей геометрическаясумма всех внутренних сил, которыми являются векторы Fл.п., Fп. л.сил, равна нулю, вследствие чего имеет место следующее выражение: Fл.п + Fп. л. = 0 ↔Fл.п = -Fп. л. ↔ Fл.п =Fп.л. = Fвз ≈ 3pe 2/2πε0b4, (3.6) где Fл.п..Fп. л. - векторысил, действующих (рис. 05.1.5) соответственно на левый диполь со стороны правого диполя и направый диполь со стороны левого диполя, имеющих одинаковый модуль
Fвз силы взаимодействия между этими диполями, т.е. левый диполь с(3.6) силойпритягивается к правомусдиполю, а правый диполь с той же самой силойпритягивается к левому диполю.
| <== предыдущая лекция | | | следующая лекция ==> |
| Занятие 8. Равновесные статистические распределения | | | Поляризация диэлектриков в электростатическом поле. Свободные, поляризационные заряды в диэлектрике 1 страница |
Дата добавления: 2016-02-14; просмотров: 1500;
