Занятие 8. Равновесные статистические распределения

Задача 04.3.1.1

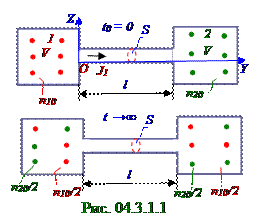
Два сосуда (рис. 04.3.1.2) одинакового V объёма соединены трубкой большой l длины и малой

S площадью поперечного сечения. В начальный t₀ = 0 момент времени в 1 левом сосуде имеется идеальный газ с n₁₀ концентрацией молекул, а в 2 правомсосуде имеется идеальный газ с n₂₀ концентрацией молекул. Давление и температура в обоих сосудах одинакова. Найти n₁⁽¹⁾ концентрацию молекул идеального газа в 1 левом сосуде как функцию t времени, считая D коэффициент диффузии молекул этого идеального газа известным. Дано: l; S; V; D/n₁⁽¹⁾(t) = ? Согласно (4.31) из раздела 04.1.0 "Физическая термодинамика" основному уравнению p = nkT молекулярно - кинетической теории n₁₀ концентрация молекул идеального газа в начальный t₀ = 0 момент времени в 1 левом сосуде равна n₂₀ концентрации молекул идеального газа в

2 правомсосуде, т.к. p давление и T температура в обоих сосудах одинакова, т.е. имеет место следующее выражение: n₁₀ = n₂₀ = n₀ .(1.1)

Количество N₀ молекул в 1 левом сосуде и в 2 правомсосуде в начальный t₀ = 0 момент времени одинаково и имеет следующее значение: N₀ = n₁₀V = n₂₀V = n₀V,(1.2) где n₁₀ - концентрация молекул идеального газа в начальный t₀ = 0 момент времени в 1 левом сосуде, равная n₂₀ концентрации молекул идеального газа в 2 правомсосуде; V -одинаковые объёмы левого и правогососудов.

газа в произвольный момент t времени имеет следующее значение: N₀ = n₁⁽¹⁾V + n₂⁽¹⁾V = n₁₀V ↔ n₁⁽¹⁾ + n₂⁽¹⁾ = n₁₀ ↔ n₂⁽¹⁾ = n₁₀ - n₁⁽¹⁾, (1.3)

где n₁⁽¹⁾ - концентрация молекул 1 идеального газа в произвольный момент t времени в 1 левом сосуде

V объёмом; n₂⁽¹⁾ - концентрация молекул 2 идеального газа в произвольный момент t времени в 1 левом сосуде V объёмом; n₁₀ - концентрация молекул идеального газа в начальный t₀ = 0 момент времени в 1 левом сосуде.

В единицу времени количество молекул 1 идеального газа, перешедших из 1 левого в 2 правый сосуд, равно количеству молекул 2 идеального газа, перешедших из 2 правого в 1 левый сосуд, т.е. в произвольный момент t времени имеет место следующее выражение: n₁⁽²⁾V = n₂⁽¹⁾V↔ n₁⁽²⁾ = n₂⁽¹⁾, (1.4) где n₁⁽²⁾ - концентрация молекул 1 идеального газа в произвольный момент t времени в 2 правомсосуде, которая образовалась за счёт перехода молекул 1 идеального газа из 1 левого в 2 правый сосуд;

n₂⁽¹⁾ - концентрация молекул 2 идеального газа в произвольный момент t времени в 1 левомсосуде, которая образовалась за счёт перехода молекул 2 идеального газа из 2 правого в 1 левый сосуд.

В произвольный момент t времени концентрация молекул 1 идеального газа в 1 левом сосуде

V объёмом равна n₁⁽¹⁾, а концентрация молекул 1 идеального газа в 2 правом сосуде V объёмом равна n₁⁽²⁾, поэтому приращение ∂n₁ концентрации молекул 1 идеального газа, отнесённое (рис. 04.3.1.1) к приращению ∂y по OY оси трубки большой l длины, по которой происходит переход молекул

1 идеального газа из 1 левого в 2 правый сосуд, имеет следующий вид: ∂n₁⁽¹⁾/∂y = (n₁⁽²⁾ - n₁⁽¹⁾)/l,(1.5)

где (n₁⁽²⁾ - n₁⁽¹⁾)/l - изменение концентрации молекул 1 идеального газа на единицу длины трубки, которое численно равно ∂n₁⁽¹⁾/∂y первой производной концентрации этих молекул 1 идеального газа по OY оси трубки большой l длины.

Подставляем в (1.5) вместо n₁⁽²⁾ концентрации молекул 1 идеального газа в произвольный момент t времени в 2 правомсосуде равную ей согласно (1.4) n₂⁽¹⁾ концентрацию молекул 2 идеального газа в тот же произвольный момент t времени в 1 левомсосуде, вследствие чего получается следующее выражение: ∂n₁⁽¹⁾/∂y = (n₂⁽¹⁾ - n₁⁽¹⁾)/l, (1.6)

Подставляем в (1.6) вместо n₂⁽¹⁾ концентрации молекул 2 идеального газа в произвольный момент t времени в 1 левомсосуде её выражение из (1.3) и получаем следующее соотношение между ∂n₁⁽¹⁾/∂x первой производной концентрации молекул 1 идеального газа по OY оси трубки большой

l длины и n₁⁽¹⁾ концентрацией молекул этого 1 идеального газа в тот же произвольный момент t времени в 1 левом сосуде V объёмом: ∂n₁⁽¹⁾/∂y = (n₁₀ - 2n₁⁽¹⁾)/l, (1.7)

где n₁₀ - концентрация молекул идеального газа в начальный t₀ = 0 момент времени в 1 левом сосуде.Диффузионный J₁ поток (4.328)из раздела 04.2.0 "Физическая термодинамика" молекул

1 идеального газа по OY оси трубки большой l длины и малой S площадью поперечного сечения с учётом (1.7) определяется из следующего выражения: J₁ = -DS(∂n₁⁽¹⁾/∂yS = -DS(n₁₀ - 2n₁⁽¹⁾)/l,(1.8)

где J₁ диффузионный поток (рис. 04.3.1.1) до момента t времени установления в результате диффузии равенства концентраций молекул 1 и 2 идеального газа в 1 левом и в 2 правом сосуде направлен по

OY оси трубки большой l длины, т.е. с учётом в (1.8) знака "-" имеет положительное значение, поскольку приращение ∂n₁ и, следовательно, ∂n₁/∂y первая производная концентрации, которую называют градиентом концентрации, молекул 1 идеального газа по этой OY оси имеет отрицательное значение.

Диффузионный J₁ поток (4.328)из раздела 04.2.0 "Физическая термодинамика" молекул

1 идеального газа по OY оси из 1 левого в 2 правый сосуд - это количество молекул 1 идеального газа, пересекающих за единицу t времени малую S площадь поперечного сечения трубки большой l длины. По своему определению этот диффузионный J₁ поток равен убыли N₁ количества молекул

1 идеального газа за единицу t времени 1 левом сосуде, т.е. равен ∂N₁/∂t первой производной от N₁ количества молекул по t времени, взятой с "-" знаком, вследствие чего имеет место следующее выражение: J₁ = - ∂N₁/∂t = - V(∂n₁⁽¹⁾/∂t), (1.9)

где J₁ диффузионный поток (рис. 04.3.1.1) до момента t времени установления в результате диффузии равенства концентраций молекул 1 и 2 идеального газа в 1 левом и в 2 правом сосуде направлен по OY оси трубки большой l длины, т.е. с учётом в (1.9) знака "-" имеет положительное значение, поскольку приращение ∂n₁⁽¹⁾ и, следовательно, ∂ n₁⁽¹⁾/∂t первая производная концентрации молекул по t времени 1 идеального газа в 1 левом сосуде V объёмом имеет отрицательное значение. Приравниваем (1.8) и (1.9), вследствие чего получается следующее дифференциальное уравнение 1 - го порядка с разделяющимися переменными: DS(n₁₀ - 2n₁⁽¹⁾)/l = V(∂n₁⁽¹⁾/∂t) ↔

↔ ∂n₁⁽¹⁾/∂t + (2DS/Vl)n₁⁽¹⁾ = (DS/Vl)n₁₀ ↔ ∂n₁⁽¹⁾/∂t + αn₁⁽¹⁾ = (α/2)n₁₀ ↔ ∂n₁⁽¹⁾/∂t = (α/2)n₁₀ - αn₁⁽¹⁾ ↔ ↔ ∂n₁⁽¹⁾/[(α/2)n₁₀ - αn₁⁽¹⁾] = ∂t. (1.10)

Используем следующую подстановку: z = [(α/2)n₁₀ - αn₁⁽¹⁾] ↔ ∂n₁⁽¹⁾ = -(1/α)∂z.(1.11)

Подставляем (1.11) в (1.10), вследствие чего получается следующее выражение: -(1/α)∂z/z = ∂t (1.12)

Интегрирование левой и правой частей (1.12) приводит к нахождению следующей зависимости n₁⁽¹⁾ концентрации молекул идеального газа в 1 левом сосуде как функции t времени:

z₂ t

-(1/α)∫∂z/z = ∫∂t ↔ ln (z₂/z₁) =- αt ↔ z₂/z₁ = e^-αt ↔ [(α/2)n₁₀ - αn₁⁽¹⁾]/ [-(α/2)n₁₀] = e^-αt ↔ z₁ 0

↔ n₁⁽¹⁾ = (n₁₀/2)(1 + e^-αt), (1.13)

где z₁ = (α/2)n₁₀ - αn₁₀ = -(α/2)n₁₀, z₂ = (α/2)n₁₀ - αn₁⁽¹⁾ - соответственно (1.11) начальное значение z параметра в начальный t₀ = 0 момент времени, когда (рис. 04.3.1.1) концентрация молекул идеального газа в 1 левом сосуде равна n₁₀, и конечное значение z параметра в произвольный t момент времени процесса диффузии, когда концентрация молекул идеального газа в 1 левом сосуде равна n₁⁽¹⁾.

Задача 04.3.1.2

Дано: l; n; d₁; d₂; χ₁; χ₂/ χ_┴ = ? χ_║ = ?

Для определения χ_┴ коэффициента теплопроводности кубика (рис. 04.3.1.3), выполненного из n пар пластинок, т.е. выполненного из неоднородного материала, при распространении q_┴н потока теплоты перпендикулярно плоскостям пластинок, т.е. в вертикальном направлении, нагреем равномерно по всей площади верхнюю грань кубика до T₁ температуры, а нижнюю грань кубика будем поддерживать при T_n температуре, при этом T₁ > T_n. Тогда q_┴н поток теплоты (4.316) из раздела 04.2.0 "Физическая термодинамика" через l² верхнюю площадь грани кубика вследствие своей непрерывности постоянен на всех поверхностях пересекаемых им пластинок и направлен по OZ оси от более горячей верхней грани кубика к менее нагретой нижней грани этого кубика.

Поток q_┴н теплоты направлен по OZ оси, т.е. он положителен, согласно (4.316) из раздела 04.2.0 "Физическая термодинамика" с учётом его постоянства на всех поверхностях, пересекаемых им пластинок, имеет следующий вид:

q_┴н = - χ₁l²dT/dx = - χ₁l²(T₁' - T₁)/d₁, q = - χ₂l²dT/dx = - χ₂l²(T₂ - T₁')/d₂;

q_┴н = - χ₁l²dT/dx = - χ₁l²(T₂' - T₂)/d₁, q = - χ₂l²dT/dx = - χ₂l²(T₃ - T₂')/d₂; .

.

q_┴н = - χ₁l²dT/dx = - χ₁l²(T _n-1' - T _n-1)/d₁, q = - χ₂l²dT/dx = - χ₂l²(T_n - T _n-1')/d₂, (2.1)

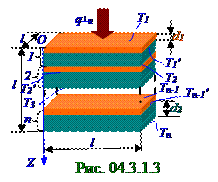
составлен кубик и которые перпендикулярно пересекает поток q_┴н теплоты; d₁, d₂ - толщина соответственно верхней и нижней 1-ой, 2-ой,…, n-ой пары пластин, на которой температура однородного материала с χ₁ коэффициентом теплопроводности линейно изменяется от значения T₁ температуры верхней поверхности до значения T₁' температуры нижней поверхности верхней пластины и от значения T₁' температуры верхней поверхности до значения T₂ температуры нижней поверхности нижней пластины, выполненной из однородного материала с χ₂ коэффициентом теплопроводности, при этом T₁ > T₂ и т.д.

Из (2.1) выражений разность температур на поверхностях каждой из пластин имеет следующий вид: T₁' - T₁ = - q_┴нd₁/χ₁l²; T₂ - T₁' = - q_┴нd₂/χ₂l²; T₂' - T₂ = - q_┴нd₁/χ₁l²; T₃ - T₂' = - q_┴нd₂/χ₂l²;

.

.

T _n-1' - T _n-1 = - q_┴нd₁/χ₁l²; T_n - T _n-1' = - q_┴нd₂/χ₂l². (2.2)

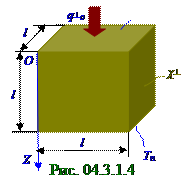
Поток q_┴о теплоты через кубик (рис. 04.3.1.4), выполненный из однородного материала с неизвестным χ_┴ коэффициентом теплопроводности, с T₁ температурой верхней грани и T_n температурой нижней грани этого кубика имеет согласно (4.316) из раздела 04.2.0 "Физическая термодинамика" следующий вид: q_┴о = - χ_┴l²dT/dx = - χ_┴l²(T_n - T₁)/l ↔ (T_n - T₁) = - q_┴о/χ_┴l, (2.4)

где l² - площадь поверхности грани кубика, которую перпендикулярно пересекает поток q_┴о теплоты; l - длина грани кубика, на которой температура однородного материала с неизвестным χ_┴ коэффициентом теплопроводности линейно изменяется от значения T₁ температуры верхней грани до значения T_n температуры нижней грани кубика, при этом T₁ > T_n.

Распределение T температуры (рис. 04.3.1.4) по толщине кубика, выполненного из однородного материала с неизвестным χ_┴ коэффициентом теплопроводности, с T₁ температурой верхней грани и T_n температурой нижней грани этого кубика, представляет собой прямую линию. Распределение T температуры по толщине кубика, выполненного из n пар пластинок, т.е. выполненного из неоднородного материала, представляет собой ломаную линию. При этом сумма приращений T₁' - T₁, T₂ - T₁', T₂' - T₂, T₃ - T₂', …, T _n-1' - T _n-1, T_n - T _n-1' температур соответственно между нижними и верхними поверхностями 1-ой, 2-ой,…, n-ой пар пластин кубика, выполненного из неоднородного материала, равняется приращению T_n - T₁ температур между верхней и нижней гранями кубика, выполненного из однородного материала, т.е. имеет место следующее равенство:

T_n - T₁ = (T₁' - T₁) + (T₂ - T₁') + (T₂' - T₂) + (T₃ - T₂') + (T _n-1' - T _n-1) + (T_n - T _n-1'). (2.5) Подставляем в (2.5) выражение (2.4) приращения T_n - T₁ температур между верхней и нижней гранями кубика, выполненного из однородного материала, и выражения (3.2) приращений

T_n - T₁ температур между верхней и нижней гранями кубика, выполненного из однородного материала, т.е. имеет место следующее равенство: T_n - T₁ = (T₁' - T₁) + (T₂ - T₁') + (T₂' - T₂) + (T₃ - T₂') +

+ (T _n-1' - T _n-1) + (T_n - T _n-1'). (2.7)

Подставляем в (2.7) выражение (2.4) приращения T_n - T₁ температур между верхней и нижней гранями кубика, выполненного из однородного материала, и выражения (2.2) приращений T₁' - T₁, T₂ - T₁', T₂' - T₂, T₃ - T₂', …, T _n-1' - T _n-1, T_n - T _n-1' температур соответственно между нижними и верхними поверхностями 1-ой, 2-ой,…, n-ой пар пластин кубика, выполненного из неоднородного материала, вследствие чего получается следующее выражение: - q_┴о/χ_┴l =

= [(- q_┴нd₁/χ₁l²) + (- q_┴нd₂/χ₂l²)] +[(- q_┴нd₁/χ₁l²) + (- q_┴нd₂/χ₂l²)] + … + [(- q_┴нd₁/χ₁l²) + (- q_┴нd₂/χ₂l²)] ↔ ↔ - q_┴о/χ_┴l = n[(- q_┴нd₁/χ₁l²) + (- q_┴нd₂/χ₂l²)]. (2.8)

Из (2.8) получаем следующее выражение χ_┴ коэффициента теплопроводности этого кубика, выполненного из однородного материала: χ_┴ = l/n[(d₁/χ₁) + (d₂/χ₂)]. (2.9)

По выражению (2.9) можно определить χ_┴ коэффициент теплопроводности кубика, выполненного из однородного материала, выраженного через параметры кубика такого же размера, но составленного из n пар пластинок, т.е. имеющего неоднородный материал, при распространении q_┴н потока теплоты перпендикулярно плоскостям пластинок, т.е. в вертикальном направлении.

Тогда q₁', q₁'', q₂', q₂'', …, q_n', q_n'' потоки теплоты (рис. 04.3.1.6) через соответственно верхнюю и нижнюю 1-ую пару пластин, верхнюю и нижнюю 2-ую пару пластин, …, верхнюю и нижнюю n-ую пару пластин согласно (4.316) из раздела 04.2.0 "Физическая термодинамика", имеет следующий вид:

q₁' = - χ₁d₁ldT/dy = - χ₁d₁l(T_n - T₁)/l, q₁'' = - χ₂d₂ldT/dy = - χ₂d₂l(T_n - T₁)/l;

q₂' = - χ₁d₁ldT/dy = - χ₁d₁l(T_n - T₁)/l, q₂'' = - χ₂d₂ldT/dy = - χ₂d₂l(T_n - T₁)/l; .

.

q_n' = - χ₁d₁ldT/dy = - χ₁d₁l(T_n - T₁)/l, q_n'' = - χ₂d₂ldT/dy = - χ₂d₂l(T_n - T₁)/l, (2.10)

где d₁l, d₂l - площади верхней и нижней поверхности 1-ой, 2-ой … n-ой пары пластин, из которых составлен кубик и которые перпендикулярно пересекают q₁', q₁'', q₂', q₂'', …, q_n', q_n'' потоки теплоты;

l - толщина верхней 1-ой, 2-ой,…, n-ой пары пластин, на которой температура однородного материала с χ₁ коэффициентом теплопроводности линейно изменяется от значения T₁ температуры левой поверхности до значения T_n температуры правой поверхности, а также толщина нижней 1-ой, 2-ой,…, n-ой пары пластин, на которой температура однородного материала с χ₂ коэффициентом теплопроводности линейно изменяется от значения T₁ температуры левой поверхности до значения T_n температуры правой поверхности, при этом T₁ > T_n.

кубик, выполненный из (рис. 04.3.1.6) неоднородного материала, т.е. когда существует следующее равенство: q_║о = q₁' + q₁'' + q₂' + q₂''+ … + q_n'+ q_n'' . (2.11) Поток q_║о теплоты через кубик (рис. 04.3.1.7), выполненный из однородного материала с неизвестным χ_║ коэффициентом теплопроводности, с T₁ температурой левой грани и T_n температурой правой грани этого кубика имеет согласно (4.316) из раздела 04.2.0 "Физическая термодинамика" следующий вид: q_║о = - χ_║l²dT/dx = - χ_║l²(T_n - T₁)/l, (2.12)

где l² - площадь поверхности грани кубика, которую перпендикулярно пересекает поток q_║о теплоты; l - длина грани кубика, на которой температура однородного материала с неизвестным χ_║ коэффициентом теплопроводности линейно изменяется от значения T₁ температуры левой грани до значения T_n температуры правой грани кубика, при этом T₁ > T_n.

Подставляем в (2.11) выражение (2.12) потока q_║о теплоты через кубик (рис. 04.3.1.7), выполненный из однородного материала с неизвестным χ_║ коэффициентом теплопроводности, и выражения (3.10) q₁', q₁'', q₂', q₂'', …, q_n', q_n'' потоков теплоты (рис. 04.3.1.6) через соответственно верхнюю и нижнюю 1-ую пару пластин, верхнюю и нижнюю 2-ую пару пластин, …, верхнюю и нижнюю n-ую пару пластин, вследствие чего получается следующее выражение:

- χ_║l²(T_n - T₁)/l = {[- χ₁d₁l(T_n - T₁)/l] + [- χ₂d₂l(T_n - T₁)/l]} + {[- χ₁d₁l(T_n - T₁)/l] + [- χ₂d₂l(T_n - T₁)/l]} +…

…+{[- χ₁d₁l(T_n - T₁)/l] + [- χ₂d₂l(T_n - T₁)/l]} ↔ χ_║l = n(χ₁d₁ + χ₂d₂). (2.13) Из (2.13) получаем следующее выражение χ_║ коэффициента теплопроводности кубика, выполненного из однородного материала , выраженного через параметры кубика такого же размера, но составленного из n пар пластинок, т.е. имеющего неоднородный материал, при распространении q_║н потока теплоты параллельно плоскостям пластинок, т.е. в горизонтальном направлении: χ_║ = n(χ₁d₁ + χ₂d₂)/l. (2.14)

Задача 04.3.1.3

Идеальный газ при нормальных условиях с известным ξ коэффициентом вязкости заполняет пространство между двумя длинными коаксиальными цилиндрами. Средний радиус цилиндров равен R, зазор между ними равен ΔR, причём ΔR << R. Внутренний цилиндр неподвижен, а внешний вращают с небольшой ω угловой скоростью по "часовой стрелке". Найти M_тр модуль и направление вектора M_тр момента сил трения, действующих на единицу длины внутреннего цилиндра.

Дано: ξ; R; ΔR; ω/ M_тр = ? Направление вектора M_тр момента сил трения ?

В данной задаче согласно параграфу "Инвариантность уравнений механики относительно преобразований Галилея" из раздела 03.0.0 "Релятивистская механика" в классической механике

координат на неподвижном внешнем цилиндре в плоскости его окружности. Тогда слои идеального газа перемещаются с вектором u линейной скорости по OY оси так, как представлено на рис.04.2.0.30 из раздела 04.2.0 "Физическая термодинамика".

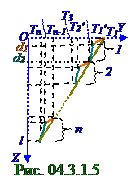
Проекция (рис. 04.3.1.8) u_R-ΔR/2 на OY ось вектора u_R-ΔR/2 линейной скорости движения по окружности слоя идеального газа, контактирующего с боковой поверхностью внутреннего цилиндра, т.е. имеющего координату y = ΔR, согласно (1.23) из раздела 01.0.0 "Физические основы механики " связана (рис. 04.3.1.8) с небольшой ω угловой скоростью вращения этого внутреннего цилиндра вокруг OZ оси следующим выражением: u_R-ΔR/2 ≈ ωR. (3.1)

Проекция (рис. 04.3.1.9) u_R+ΔR/2 на OY ось вектора u_R+ΔR/2 слоя идеального газа, контактирующего с боковой поверхностью неподвижного цилиндра, т.е. имеющего координату y = 0, равна нулю, вследствие чего имеет место следующее выражение: u_R+ΔR/2 = 0. (3.2)

Первая du/dx производная u проекции (рис. 04.3.1.9) на OY ось вектора u линейной скорости движения по окружности слоёв идеального газа, вследствие линейной зависимости этой u проекции от x координаты, имеет с учётом (3.1), (3.2) следующий вид: du/dx = (u_R-ΔR/2 - u_R+ΔR/2)/ΔR = ωR/ΔR,(3.3)

вектор ΔK приращения импульса с проекцией ΔK на OX ось, имеющей с учётом (4.3) следующее значение: ΔK = -ς(du/dx)S ≈ -ς2πωR²L/ΔR,(3.4)

где S ≈ 2πRL - площадь боковой поверхности внутреннего цилиндра, имеющей L длину; ς - коэффициент (4.298) из раздела 04.2.0"Физическая термодинамика" вязкости идеального газа, заполняющего пространство между двумя длинными коаксиальными цилиндрами.

Проекция ΔK на OY ось вектора ΔK приращения импульса в (3.4) отрицательна потому, что этот вектор ΔK приращения импульса (рис. 04.3.1.9) направлен противоположно OY оси, т.е. вследствие явления вязкости или внутреннего трения слои идеального газа, двигающиеся с бόльшей по модулю скоростью, испытывают торможение от слоёв идеального газа, двигающихся с меньшей по модулю скоростью. Поэтому монослой идеального газа, покрывающий вращающийся вокруг OZ оси с небольшой ω угловой скоростью внутренний цилиндр, испытывает торможение от соседних слоёв идеального газа, двигающихся с меньшей по модулю скоростью. Следовательно, испытывает торможение от соседних слоёв идеального газа вращающийся вокруг OZ оси с небольшой ω угловой скоростью внутренний цилиндр и к его боковой поверхности (рис. 04.3.1.9) в единицу t времени от слоя идеального газа,контактирующего с этой боковой поверхностью внутреннего цилиндра, переносится вектор ΔK приращения импульса с (4.4) проекцией ΔK на OY ось.

Вектор ΔL приращения момента импульса (рис. 04.3.1.9), переносимой к вращающемуся вокруг

OZ оси с небольшой ω угловой скоростью внутреннему цилиндру, в единицу t времени от слоя идеального газа,контактирующего с боковой поверхностью внутреннего цилиндра, согласно (1.67) из раздела 01.0.0 "Физические основы механики " имеет следующий вид: ΔL = [R-ΔR/2, ΔK],(3.5)

где R-ΔR/2 - радиус-вектор, направленный из B точки, лежащей (рис. 04.3.1.8) на OZ оси вращения внешнего цилиндра и перпендикулярный этой OZ оси, в A точку (рис. 04.3.1.9) приложения вектора ΔK приращения импульса, переносимого к боковой поверхности вращающегося вокруг OZ оси с небольшой ω угловой скоростью внутреннего цилиндра в единицу t времени, от слоя идеального газа,контактирующего с этой боковой поверхностью внутреннего цилиндра.

Вектор ΔL приращениямомента импульса (рис. 04.3.1.8), переносимой к вращающемуся вокруг OZ оси с небольшой ω угловой скоростью внутреннему цилиндру, в единицу t времени от слоя идеального газа,контактирующего с этой боковой поверхностью внутреннего цилиндра, согласно (1.67) из раздела 01.0.0 "Физические основы механики ", составляет (3.5) с

R-ΔR/2, K векторами правую тройку векторов, вследствие чего этот вектор ΔL приращениямомента направлен перпендикулярно (рис. 04.3.1.9) плоскости от наблюдателя.

Вектор ΔL приращения момента импульса (рис. 04.3.1.9) переносится к вращающемуся вокруг OZ оси с небольшой ω угловой скоростью внутреннему цилиндру в единицу t времени, поэтому (3.5) выражение численно равна (1.75) из раздела 01.0.0 "Физические основы механики "первой производная по t времени от вектора L момента, приложенного к этой неподвижной боковой поверхности, вследствие чего имеет место следующее выражение: dL/dt = [R-ΔR/2, ΔK]. (3.6) Согласно (1.76) из раздела 01.0.0 "Физические основы механики "закону изменения момента импульса механической системы первая производная по t времени от (4.6) вектора L момента импульса, переносимого к неподвижной боковой поверхности (рис. 04.3.1.9) внутреннего цилиндра равна вектору M_тр момента сил трения, действующих на внутренний цилиндр, вследствие чего с учётом (4.6) имеет место следующее выражение: dL/dt = M_тр↔ [R-ΔR/2, ΔK] = M_тр, (3.7)

где M_тр - вектормомента сил трения, действующих на внутренний цилиндр, коллинеарен вектору ΔL приращения момента импульса, переносимого к вращающемуся вокруг OZ оси с небольшой

ω угловой скоростью внутреннему цилиндру и направлен с ним в одну сторону. Этот вектор M_тр момента сил трения возникает вследствие трения слоёв идеального газа, контактирующих с боковой поверхностью внутреннего цилиндра и вращающихся (рис. 04.3.1.9) по часовой стрелки.

Проекция M_тр на OZ ось вращения внутреннего цилиндра вектора M_тр момента сил трения, действующих на этот внутренний цилиндр, вследствие перпендикулярности (рис. 04.3.1.9) векторов R-ΔR/2, ΔK имеет с учётом (3.7), (3.4) и (3.1) следующий вид:

M_тр ≈ RΔK = - ςR(du/dy)S = - ς2πωR³L/ΔR, (3.8) где знак "-" в проекции M_тр на OZ ось вращения внутреннего цилиндра вектора M_тр момента сил трения имеет место потому, что этот вектор M_тр момента сил трения направлен (рис. 04.3.1.9) противоположно направлению вектора ω угловой скорости вращения внутреннего цилиндра, который вращается вокруг OZ оси с небольшой ω угловой скоростью против часовой стрелки, т.е. вращается в положительную сторону.

Проекция M_тр на OZ ось вращения на единицу L длины внутреннего цилиндра вектора

M_тр момента сил трения, действующих на этот внутренний цилиндр, имеет с учётом (3.8) следующий вид: M_тр/L ≈ - 2πςωR³/ΔR, (3.9)

где знак "-" означает, что вектор M_тр момента сил трения, действующих на внутренний цилиндр, направлен в противоположную OZ оси сторону. При возвращении схемы (рис. 04.3.1.8) расчёта к виду, указанному в условии задачи, т.е. внутренний цилиндр неподвижен, а внешний вращают с небольшой

ω угловой скоростью, направление вектора M_тр/L момента сил трения, действующих на единицу L длины внутреннего цилиндра, и его проекция M_тр/L на OZ ось вращения, не изменяют своего направления и (3.9) значения, если внешний цилиндр вращать с небольшой ω угловой скоростью по "часовой стрелке".

Задача 04.3.1.4

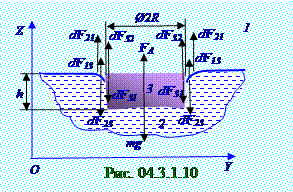
На рис. 04.3.1.10 dF₁₃ (рис. 04.3.0. 46) из раздела 04.3.0 " Физическая термодинамика" - это вектор элементарной силы поверхностного натяжения плёнки 1 воздуха на боковой поверхности

3 алюминиевого диска, направленная в сторону уменьшения площади контакта этой плёнки 1 воздуха с боковой поверхностью 3 алюминиевого диска, т.е. вверх. Вектор dF₁₃ элементарной силыприложен к элементарному участку dl длиной (рис. 04.3.0.47) из раздела 04.3.0 " Физическая термодинамика" поверхности плёнки 1 воздуха на боковой поверхности 3 алюминиевого диска, имеющему при виде сверху форму окружности. Этот вектор dF₁₃ элементарной силывызван взаимодействием боковой поверхности 3 алюминиевого диска с граничащей по этой поверхности плёнкой 1 воздуха. По III закону Ньютона к элементарному участку dl длинойбоковой поверхности 3 алюминиевого диска, имеющему при виде сверху форму окружности, из-за взаимодействия с плёнкой 1 воздуха, граничащейпо этой боковой поверхности с 3 алюминиевого диска, приложен вектор dF₃₁ элементарной силы, равный по модулю и противоположный по направлению вектору dF₁₃ элементарной силы. На рис. 04.3.1.10 dF₂₃ (рис. 04.3.0. 46) из раздела 04.3.0 "Физическая термодинамика" - это вектор элементарной силы поверхностного натяжения плёнки несмачивающей 2 жидкости на боковой поверхности 3 алюминиевого диска, направленный в сторону уменьшения площади контакта этой плёнки 2 жидкости с боковой поверхностью 3 алюминиевого диска, т.е. вниз. Вектор dF₂₃ элементарной силы приложен к элементарному участку dl длиной(рис. 04.3.0.47) из раздела 04.3.0

"Физическая термодинамика" поверхности плёнки несмачивающей 2 жидкости на боковой поверхности 3 алюминиевого диска,имеющему при виде сверху форму окружности. Этот вектор dF₂₃ элементарной силы вызван взаимодействием боковой поверхности 3 алюминиевого дискас граничащей по этой поверхности плёнкой несмачивающей 2 жидкости. По III закону Ньютона к элементарному участку dl длинойбоковой поверхности 3 алюминиевого диска, имеющему при виде сверху форму окружности, из-за взаимодействия с плёнкой 2 жидкости, граничащейпо этой боковой поверхности с 3 алюминиевым диском,приложен вектор dF₃₂ элементарной силы, равный по модулю и противоположный по направлению вектору dF₂₃ элементарной силы.

На рис. 04.3.1.10 dF₂₁ (рис. 04.3.0. 46) из раздела 04.3.0 " Физическая термодинамика" - это вектор элементарной силы поверхностного натяжения на границе раздела 2 вода - 1 воздух, направленный по касательной к поверхности раздела 2 вода - 1 воздух в сторону уменьшения площади этой поверхности. По условию задачи смачивание полное, поэтому вектор dF₂₁ элементарной силы приложен к пленке 2 воды и направлен по боковой поверхности 3 алюминиевого диска вверх, т.е. краевой (рис. 04.3.0. 46) из раздела 04.3.0 " Физическая термодинамика" θ уголмежду боковой поверхностью 3 алюминиевого диска и поверхностью раздела 2 вода - 1 воздух равен 180º. Сумма проекций dF₂₁, dF₂₃ и dF₁₃ на OZ ось векторов dF₂₁, dF₂₃ и dF₁₃ трёх элементарных сил (4.380) из раздела 04.3.0 " Физическая термодинамика" для случая механического равновесия элементарного участка dl длинойграницы 2 вода - 1 воздух, несмачивающей (рис.8.1) боковую поверхностью 3 алюминиевого диска, имеет следующий вид: dF₂₁ + dF₁₃ - dF₂₃ = 0. (4.1) Проекцию dF₂₁ на OZ ось (рис. 04.3.1.10) вектора dF₂₁ элементарной силы поверхностного натяжения выражаем (4.376) из раздела 04.3.0 "Физическая термодинамика" через σ₂₁ коэффициент поверхностного натяжения на границе элементарного участка dl длиной(рис. 04.3.0.47) из раздела 04.3.0 " Физическая термодинамика" на границе поверхности раздела 2 вода - 1 воздух, вследствие чего получаем следующее выражение: dF₂₁ = σ₂₁dl.(4.2) Подставляем (4.2) в (4.1) и получаем следующее выражение результирующей dF_y = dF₁₃ - dF₂₃ проекции OZ ось вектора dF₁₃ элементарной силы поверхностного натяжения плёнки 1 воздуха на боковой поверхности 3 алюминиевого диска и вектора dF₂₃ элементарной силы поверхностного натяжения плёнки несмачивающей 2 жидкости на боковой поверхности 3 алюминиевого диска: σ₂₁dl +(dF₁₃ - dF₂₃) = 0 ↔ σ₂₁dl + dF_y = 0. (4.3) Результирующая dF_y = dF₁₃ - dF₂₃ проекция векторов элементарных сил поверхностного натяжения, действующих на элементарный участок dl длиной 2 водысо стороны поверхности 3 алюминиевого диска отрицательна, т.к. dF₂₃ > dF₁₃. Поэтому результирующий вектор dF_y элементарных сил поверхностного натяжения, действующих на элементарный участок dl длиной 2 водысо стороны поверхности 3 алюминиевого диска, направлен вниз, т.е. в отрицательную сторону OZ оси.

Равный по модулю и противоположный по направлению результирующий вектор dF_y′ элементарных сил поверхностного натяжения, действующий на элементарный участок dl длинойбоковой поверхности 3 алюминиевого дискасо стороны 2 вода - 1 воздух, по III закону Ньютона направлен в положительную сторону OZ оси.

Проекция dF_y′ на OY ось результирующего вектора dF_y′ элементарных сил поверхностного натяжения, действующих на элементарный участок dl длинойбоковой поверхности 3 алюминиевого дискасо стороны 2 вода - 1 воздух, с учётом (4.3) имеет следующее положительное значение: dF_y′ = σ₂₁dl. (4.4) Проекция dF_y′ на OZ ось численно равна модулю dF_y′ результирующего вектора dF_y′ элементарных сил поверхностного натяжения, действующих на элементарный участок dl длинойбоковой поверхности 3 алюминиевого дискасо стороны 2 вода - 1 воздух, т.к. этот вектор направлен в положительную сторону OZ оси.

Боковая поверхность 3 алюминиевого диска, на элементарный участок dl длинойкоторой действует вектор dF_y′ элементарных сил поверхностного натяжения со стороны воды 2 вода - 1 воздух, представляет собой цилиндрическую поверхность с R радиусом. Поэтому с учётом равенства векторов dF_y′ каждой элементарной силы поверхностного натяжения, действующих на элементарный участок dl длинойповерхности 3 алюминиевого дискасо стороны 2 вода - 1 воздух, модуль F_y′ результирующего вектора F_y′ сил поверхностного натяжения по всей окружности этой боковой поверхности 3 алюминиевого диска 2πR длиной имеет следующий вид: 2πR F_y′ = ∫ dF′. (4.5) 0 Подставляем (4.4) в (4.5), производим интегрирование и получаем следующее выражение модуля F_y′ результирующего вектора F_y′ сил поверхностного натяжения, действующих на всю боковую поверхность 3 алюминиевого дискасо стороны 2 вода - 1 воздух: F_y′ = σ₂₁2πR. (4.6) Таким образом на 3 алюминиевый диска (рис. 04.3.1.10) действуют три силы: сила поверхностного натяжения с вектором F_y′, направленным в положительную сторону OZ оси, сила Архимеда с вектором F_A, направленным тоже в положительную сторону OZ оси, и сила тяжести с вектором mg, направленным в отрицательную сторону OZ оси.

С учётом механического равновесия 3 алюминиевого диска(рис. 04.3.1.10) сумма проекций на OZ ось векторов всех трёх сил равна нулю, вследствие чего получаем следующее выражение: 0 = σ₂₁2πR + πR²hρ_вg - πR²hρg, (4.7) где πR²hρ_вg - проекция вектора F_A силы Архимеда на OZ ось, ρ_в - плотность воды; σ₂₁2πR - проекция на OZ ось (5.6) вектора F_y′ силы поверхностного натяжения; πR²hρg - проекция вектора mg силы тяжести на OZ ось, ρ - плотность алюминия.

Решаем (4.7) относительно σ₂₁ коэффициента поверхностного натяжения на границе поверхности раздела вода 2 - воздух 1, вследствие чего получаем следующее выражение:

σ₂₁ = Rhg(ρ - ρ_в)/2.(4.8) Задача 04.3.1.5

Какую А работунадо совершить, чтобы надуть изотермически мыльный пузырь R радиусом. Известны σ коэффициент поверхностного натяжения на границе воздух - мыльная плёнка и р₀ давление окружающего воздуха. Дано: P₀; σ; R /A = ?

Давление (рис. 04.3.1.11) P_ж1 во внутреннем слое жидкости мыльного пузыря, являющейся вогнутой (рис. 04.3.1.50) из раздела 04.3.0 "Физическая термодинамика" поверхностной плёнкой на границе раздела внутренний слой жидкости мыльного пузыря - воздух P_г1 давлением внутри этого мыльного пузыря, имеет согласно (4.404) из раздела 04.3.0 " Физическая термодинамика" следующий вид: P_ж1 - P_г1 = 2σ/R ↔ P_ж1 = P_г1 + ΔP = P_г1 + (2σ/R₁),(5.1)

раздела внутренний слой P_ж1 давлением жидкости мыльного пузыря - воздух P_г1 давлением внутри этого мыльного пузыря.

Давление P_ж2 в наружном слое жидкости мыльного пузыря, являющейся выпуклой

(рис. 04.3.1.51) из раздела 04.3.0 "Физическая термодинамика" поверхностной плёнкой на границе раздела наружный слой жидкости мыльного пузыря - воздух P_г0 давлением окружающей среды имеет согласно (4.382) из раздела 04.3.0 "Физическая термодинамика" следующий вид:

P_ж2 - P_г0 = 2σ/R ↔ P_ж2 = P_г0 + ΔP = P_г0 + (2σ/R₂),(5.2)

где ΔP = 2σ/R > 0 - дополнительное давление на границе раздела внешний слой P_ж2 давлением жидкости мыльного пузыря - воздух P_г0 давлением вокруг этого мыльного пузыря больше нуля вследствие того, что R₂ > 0 радиус сферической выпуклой поверхности внешнего слоя этого мыльного пузыря больше нуля; σ - (4.389) из раздела 04.3.0 " Физическая термодинамика" коэффициент поверхностного натяжения на границе сферической выпуклой поверхности R₂ радиусом на границе раздела внешний слой P_ж2 давлением жидкости мыльного пузыря - воздух P_г0 давлением вокруг этого мыльного пузыря.

Согласно закону Паскаля давление в тонком слое жидкости мыльного пузыря должно быть одинаковым, поэтому приравниваем (5.1) P_ж1 давление во внутреннем слое жидкости мыльного пузыря (5.2) P_ж2 давлению в наружном слое жидкости мыльного пузыря, и далее определяем P_г1 давление внутри мыльного пузыря, которое имеет следующий вид: P_ж1 = P_ж2 ↔ P_г1 + (2σ/R₁) = P_г0 + (2σ/R₂) ↔ P_г1 = P_г0 + (4σ/R),(5.3) где R ≈ |R₁| ≈ R₂ - средний радиус мыльного пузыря, примерно равный вследствие малой толщины его стенки модулю отрицательного R₁ радиуса сферической поверхности внутреннего слоя и положительного R₂ радиуса сферической поверхности наружного слоя жидкости мыльного пузыря.

При надувании (рис. 04.3.1.11) изотермически мыльного пузыря величина его r радиуса увеличивается от нуля до R значения. Согласно выражению (4.12) из раздела 04.1.0 "Физическая термодинамика" работы термодинамической системы в δA дифференциальном виде и A интегральном виде при надувании мыльного пузыря R радиусом термодинамическая система мыльный пузырь - воздух P_г0 давлением окружающей среды совершает следующую работу:

V₂ R A = ∫ P(V)dV = ∫[P_г0 +(4σ/r)]4πr²dr = 4πR²[2σ + (1/3)P_г0R], (5.4)

V₁ 0

где P(V) = (P_г0 + 4σ/r) - зависимость давления внутри мыльного пузыря от его V объёма, т.е от r радиуса мыльного пузыря, изменяющегося от нуля до заданного R значения; dV = 4πr²dr - элементарный объём, равный (рис. 04.3.1.11) шаровому слою элементарной dr толщины.

Согласно условию мыльный пузырь надувается при постоянной температуре, поэтому σ коэффициент поверхностного натяжения во время всего процесса остаётся постоянным.

Задача 04.3.1.6

соответственно. Найти χ₀ коэффициент теплопроводности однородного стержня l₁ + l₂ длины, поток теплоты через поперечное сечение которого при равных температурах торцов составного и однородного стержней будет одинаков. Поток теплоты направлен вдоль стержня, т.е.без потерь через стенки. Ответ: χ₀ = (l₁ + l₂)/[(l₁/χ₁) + (l₂/χ₂)]. Дано: l₁; l₂; χ₁; χ₂/ χ₀ = ?

При условии равномерного распределения T температуры вдоль левой и правой части составного стержня (рис. 04.3.1.12, а) соответственно l₁, l₂ длиной с учётом температуры T₁, T₂, T₃

на торцах этого составного стержня и при этом T₁ > T₂ > T₃ имеет место следующее выражение: dT/dy = (T₂ - T₁)/l₁, если 0 < y < l₁; (8.1) dT/dy = (T₃ - T₂)/l₂, если l₁ < y < l₂ . (8.2) При условии равномерного распределения T температуры вдоль однородного стержня (рис. 04.3.1.12, б) длиной l₁ + l₂ с учётом T₁, T₃ температурына торцах этого однородного стер