Занятие 8. Равновесные статистические распределения.

Задача 7-1

Задача 04.2.1.1

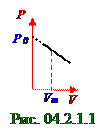
Идеальный газ с γ показателем адиабаты совершает обратимый процесс со следующей зависимостью p давления от V объёма: P = P₀ - αV, где p₀ и α - положительные постоянные. При каком значении V_m объёма S энтропия идеальногогаза окажется максимальной и равной S_max?

Дано: γ; P =P₀ - αV; S(V_m) = max/V_m = ?

термодинамика" S энтропии согласно параграфу "Термодинамическая энтропия для обратимого термодинамического процесса" с учётом количества ν = M/μ вещества и (1.1) имеет следующий вид: dS ={[C_v(M/μ)dT]/T} + [(M/μ)RdV]/V] = [(νR)/(γ - 1)](dT/T) + νR(dV/V). (1.2)

V объёма в (1.3) и получаем выражение dT дифференциала от T температуры: dT = (P₀ - 2αV)dV/νR. (1.5) Делим (1.5) на (1.3) T = PV/νR c подстановкой в него P = P₀ - αV и получаем следующее выражение относительного dT/T дифференциалатемпературы: dT/T = (P₀ - 2αV)dV/(P₀ - αV)V. (1.6) Подставляем (1.6) в (1.2) и получаем следующее выражение dS/dV первой производной

S энтропии в зависимости от V объёма: dS/dV = (νR){[(p₀ - 2αV)/(γ - 1)( p₀ - αV)V] + (1/V)}. (1.7) Энтропия S будет равна своей S_max максимальной величине при значении V_m объёма, когда dS/dV первая производная в (6.7) равна нулю, вследствие чего имеет место следующее выражение: dS/dV|_Vm = 0 ↔ {[(p₀ - 2αV_m)/(γ - 1)( p₀ - αV_m)V_m] + (1/V_m)} = 0 ↔ V_m = γp₀/α(γ - 1), м³. (1.8) Задача 04.2.1.2

Один ν = 1 моль газа Ван - дер - Ваальса, имевший V₁ объём и T₁ температуру, переведён в состояние с V₂ объёмом и T₂ температурой. Найти ΔS приращение S энтропии газа, считая известной

b константу газа Ван - дер - Ваальса, с помощью которой переходят от V' объёма сосуда, свободного от молекул газа Ван - дер - Ваальса, к V объёму газа Ван - дер - Вальса, а также считая известной

C_V молярную теплоемкостьпри постоянном V объёме этого газа Ван - дер - Вальса.

Дано: ν; V₁; T₁; V₂; T₂; C_V/ ΔS = ?

Свободный (рис. 04.2.1.2) от молекул V₁′, V₂′ объёмы, т.е. объёмы (4.110) из раздела 04.1.0 "Физическая термодинамика" идеального газа, эквивалентного по своим свойствам ван - дер -

ваальсовскому газу и с соответственно P₁, P₂ давлением на стенки сосуда и V₁, V₂ объёмом в

1-ом состоянии и во 2-ом состоянии с учётом ν = 1 моль количества газа имеет следующий вид:

V₁′ = V₁ - b; V₂′ = V₂ - b. (2.1)

Приращение ΔS = S₂ - S₁ энтропии идеального газа, эквивалентного по своим свойствам ван - дер - ваальсовскому газу, при переходе в обратимом процессе из (рис. 04.2.1.2) 1-ого состояния во

2-ое состояние согласно (4.155) из раздела 04.1.0 "Физическая термодинамика" имеет следующий вид: ΔS = ν[C_Vln(T₂/T₁) + Rln(V₂′/V′₁)]. (2.2) Подставляем (2.1) V₁′, V₂′ объёмы идеального газа, эквивалентного по своим свойствам ван - дер

Задача 04.2.1.3

Плотность ρ смеси He гелия и N₂ азота при нормальных условиях имеет значение: ρ = 0,60 г/л. Найти n_He концентрацию молекул He гелия в этой смеси. Дано: ρ, p₀, T₀, m_He, m_N2/n_He = ?

Плотности ρ_He гелия He, ρ_N2 азота N₂ c учётом масс их молекул соответственно m_He, m_N2, а также с учётом концентраций n_He, n_N2 этих молекул имеют следующий вид: ρ_He = n_Hem_He; ρ_N2 = n_N2m_N2.(3.1) Согласно закону Дальтона ρ плотность смеси He гелия и N₂ азота равна сумме плотностей каждого из этих газов в отдельности, из чего с учётом (3.1) получаем следующее выражение

n_N2 концентрацию молекул азотав этой смеси:

ρ = ρ_He + ρ_N2 = n_Hem_He + n_N2m_N2 ↔ n_N2 = (ρ - n_Hem_He)/m_N2.(3.2) Парциальные P_He, P_N2 давления соответственно молекул с n_He, n_N2 концентрациями соответственно He гелия и N₂ азота в смеси этих газов согласно основному (4.30) из раздела 04.1.0 "Физическая термодинамика" уравнению молекулярно - кинетической теории при T₀ нормальной температуре окружающей среды с учётом k = 1,38·10^-23 Дж/K постоянной Больцмана имеют следующий вид : P_He = n_HekT₀; P_N2 = n_N2kT₀. (3.3) Согласно закону Дальтона P₀ нормальное давлениесмеси равна сумме P_He, P_N2 парциальных (3.3) давлений соответственно He гелия и N₂ азота, вследствие чего имеет место следующее выражение: P₀ = P_He + P_N2 ↔ n_N2kT₀ = P₀ - n_HekT₀. (3.4) Подставляем (3.2) n_N2 концентрацию молекул азота в (3.4) и получаем следующее выражение

n_He концентрациb молекул He гелия в его смеси с N₂ азотом: (ρ - n_Hem_He)kT₀/m_N2 = P₀ - n_HekT₀ ↔ n_He = [(P₀/kT₀) - (ρ/m_N2)]/[1- (m_He/ m_N2)], 1/м³, (3.5) где ρ - плотность смеси He гелия и N₂ азота при её P₀ нормальном давлении и T₀ нормальной температуре окружающей среды.

Задача 04.2.1.4

Во сколько k раз надо расширить адиабатически идеальный газ, состоящий из жёстких двухатомных молекул, чтобы их v_кв средняя квадратичная скорость уменьшилась в η = 1,5 раза.

Дано: v_кв1/v_кв2 = η; k = ?

Отношение v_кв1,v_кв2 средних квадратичных скоростей согласно (4.34) из раздела 04.1.0 "Физическая термодинамика" с учётом μ молярной массы идеального газа при T₁, T₂ температурах соответственнои условия задачи имеет следующий вид:

η = v_кв1/v_кв2 = (3RT₁/ μ)^1/2/(3RT₂/ μ)^1/2 = (T₁/T₂)^1/2 ↔ T₁/T₂ = η². (4.1) Уравнение Пуассона (4.68) из раздела 04.1.0"Физическая термодинамика" в параметрах

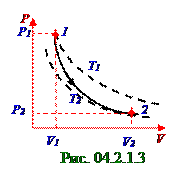
P давления и V объёма (рис. 04.2.1.3) в 1-ом состоянии и во 2-ом состоянии с учётом cвязи (4.67) из раздела 04.1.0 "Физическая термодинамика" γ показателя адиабаты с i = 5 количеством степеней свободы жёстких двухатомных молекул идеального газа имеет следующий вид:

P₁V₁^γ = P₂V₂^γ ↔ P₁V₁^{(i + 2)/i} = P₂V₂^{(i + 2)/i} ↔ P₁/P₂ =( V₂/V₁) ^{(i + 2)/i}. (4.2) Уравнение (4.13) из раздела 04.1.0"Физическая термодинамика" Клапейрона - Менделеева газа с учётом постоянства ν количества этого газа при переходе из 1-ого состояния с V₁ объёмом и

T₁ температурой во 2-ое состояние с V₂ объёмом и T₂ температурой имеет следующий вид: P₁V₁/T₁ = P₂V₂/T₂ ↔ P₁/P₂ = (V₂/V₁) T₁/T₂. (4.3) Подставляем (4.1) в (4.3) и получаем следующую связь P₁/P отношения давлений во 2-ом состоянии и в 1-ом состоянии идеального газа с (v_кв1/v_кв2)² = η² квадратом отношения v_кв средних квадратичных скоростей жёстких двухатомных молекул: P₁/P₂ = (V₂/V₁)η². (4.4)

Задача 04.2.1.5

Найти δN/N относительное число молекул идеального газа, v модули векторов v скоростей которых отличаются не более, чем на δη = 1% от значения: а) наиболее v_вер вероятной скорости;

попадания заданных значений v модулей векторов v скоростей молекул идеального газа, имеющего

T температуру, без учёта направлений их движения в единичный интервал измерений, например, равна вероятности попадания v модулей векторов v скоростей молекул идеального газа в интервал

100…101 м/с значений.

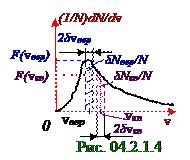
Количество δN_вер молекул, v модули векторов v скоростей которых отличаются не более, чем на δη = 1% от наиболее v_вер вероятного значения скорости, есть большое число, поэтому его отношение к полному N числу молекул в данной массе газа равняется согласно (4. 219) из раздела 04.2.0 "Физическая термодинамика" δP(v_i) вероятности события попадания v модулей векторов v скоростей молекул идеального газа в интервал 2δv_вер (рис. 04.2.1.4) скоростей.

Интервал 2δv_вер скоростей по отношению к v_вер вероятной скорости составляет 0,02 части, т.е. малую величину, поэтому приближённое значение δP(v_i) вероятностисобытия попадания v модулей векторов v скоростей молекул идеального газа в 2δv_вер интервал скоростей равно (рис. 04.2.1.4) площади прямоугольника под графиком (1/N)dN/dv плотности вероятности v модулей векторов v скоростей молекул идеального газа с высотой, равной F(v_вер) ординате, и шириной, равной 2δv_вер интервалу этих скоростей. Приближённое значение δP(v_i) вероятностисобытия попадания v модулей векторов

v скоростей молекул идеального газа в 2δv_вер интервал скоростей согласно (4.267) из раздела 04.2.0 "Физическая термодинамика" и с учётом (5.1) имеет следующий вид: δP(v_i) = δN_вер/N ≈ F(v_вер)2δv_вер = 2(m/2πkT)^3/2 exp(-mv²/2kT) 4πv² δv_вер. (5.2) Для решения а) пункта условия задачи, а именно: найти δN/N относительное число молекул идеального газа, v модули векторов v скоростей которых отличаются не более, чем на δη = 1% от значения наиболее v_вер вероятной скорости, в выражении (5.2) следует учесть, что v есть модуль векторов v скоростей молекул идеального газа, мало отличающихся от v_вер вероятной скорости, поэтому этот v модуль векторов v скоростей молекул идеального газа можно заменить на v_вер вероятную скорость, которая согласно (4.269) из раздела 04.2.0 "Физическая термодинамика" имеет следующий вид: v = v_вер = (2kT/m)^1/2. (5.3) Связь δv_вер абсолютных отклонений v модулей векторов v скоростей молекул идеального газа относительно v_вер вероятной скорости с их δη относительным отклонением имеет следующий вид: δη = δv_вер/v_вер ↔ δv_вер = δηv_вер = (2kT/m)^1/2δη. (5.4) Подставляем (5.3), (5.4) в (5.2) и получаем следующее выражение (рис.5.1) δN_вер/N относительного числа молекул идеального газа, v модули векторов v скоростей молекул идеального газа которых отличаются не более, чем на δη = 1% от значения v_вер вероятной скорости: δN_вер/N = [8/(π)^1/2]e^-1δη. (5.5) Для решения б) пункта условия задачи, а именно: найти δN/N относительное число молекул идеального газа, v модули векторов v скоростей которых отличаются не более, чем на δη = 1% от значения средней v_кв квадратичной скорости, в выражении (5.2) следует учесть, что v есть модуль векторов v скоростей молекул идеального газа, мало отличающихся от v_кв квадратичной скорости, поэтому этот v модуль векторов v скоростей молекул идеального газа можно заменить на v_кв квадратичную скорость, которая согласно (4.34) из раздела 04.1.0"Физическая термодинамика" имеет следующий вид: v = v_кв = (3kT/m)^1/2. (5.6) Связь абсолютных δv_кв отклонений v модулей векторов v скоростей молекул идеального газа относительно v_кв среднейквадратичной скорости с их δη относительным отклонением имеет следующий вид: δη = δv_кв /v_кв ↔ δv_кв = v_квδη = (3kT/m)^1/2δη. (5.7) Подставляем (5.6), (5.7) в (5.2) и получаем следующее выражение относительного (04.2.1.4) δN_кв/N числа молекул идеального газа, v модули векторов v скоростей которых отличаются не более, чем на δη = 1% от значения средней v_кв квадратичной скорости: δN_кв/N = 12(3/2π)^1/2 e^-3/2δη. (5.8)

Задача 04.2.1.6

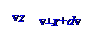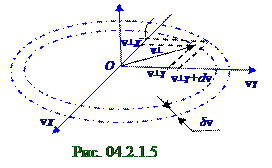
интервале значений скоростей по Ov_X оси координат v_┴X проекций на эту Ov_X ось вектора v_┴ скоростей молекул, находящихся в Ov_X, Ov_Y плоскости, имеет следующий вид:

f (v_┴X) = (m/2πkT)^1/2exp(-mv_┴X ²/2kT ). (6.1)

Функция (4.260) из раздела 04.2.0 "Физическая термодинамика" f(v_┴Y) плотности вероятности, которая численно равна вероятности нахождения в единичном интервале значений скоростей по

Ov_Y оси координат v_┴Y проекций на эту Ov_Y ось вектора v_┴ скоростей молекул, находящихся в Ov_X, Ov_Y плоскости, имеет следующий вид: f (v_┴Y) = (m/2πkT)^1/2exp(-mv_┴Y ²/2kT ). (6.2)

Cовместная (4. 228) из раздела 04.2.0 "Физическая термодинамика" f (v_┴X, v_┴Y ) функция плотности вероятности, которая численно равна вероятности одновременного нахождения в единичном интервале значений скоростей по Ov_X, Ov_Y осям координат v_┴X, v_┴Y проекций на эти Ov_X, Ov_Y оси вектора v_┴ скоростей молекул, находящихся в Ov_X, Ov_Y плоскости, имеет (6.1), (6.2) с учётом статистической независимости v_┴X и v_┴Y проекций скоростей молекул идеального газа m массой следующий вид: f(v_┴X, v_┴Y ) = f (v_┴X)f (v_┴Y) = (m/2πkT)exp[-m(v_┴X ²+ v_┴Y ²) /2kT] =

= (m/2πkT)exp(-mv_┴²/2kT), (6.3) где v_┴ = (v_┴X ²+ v_┴Y ²)^1/2 - заданное значение модуля вектора v_┴ скорости молекулы идеального газа, перпендикулярного в пространстве скоростей Ov_Z оси.

Относительное число δN/N молекулидеального газа m массой, v_┴ модуль вектора v_┴ скоростей которых, находящихся в Ov_X, Ov_Y плоскости, имеет значения v_┴ - (δv/2) ≤ v_┴ ≤ v_┴ + (δv/2) равно с учётом (6.3) следующей величине δP(v_┴X, v_┴Y ) вероятности:

δP(v_┴X, v_┴Y ) = δN/N = f(v_┴X, v_┴Y )2πv_┴δv = (m/2πkT)exp(-mv_┴²/2kT) 2πv_┴δv =

= (m/kT)exp(-mv_┴²/2kT)v_┴δv, (6.4) где 2πv_┴δv - площадь кольца (рис. 04.2.1.5) в Ov_X, Ov_Y плоскости скоростей; N - полное число молекул m массой в объёме идеального газа T температурой, в которой измеряются скорости молекул;

v_┴ - заданное значение модуля вектора v_┴ скорости молекулы идеального газа, перпендикулярного в пространстве скоростей Ov_Z оси.

Задача 04.2.1.7

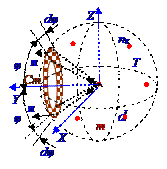
Ответ: η_dφ = n_к(2kT/πm)^1/2sinφcosφdφ, η₀ = n_к<v>/4, где <v>= (8kT/πm)^1/2 - среднее арифметическое значение v_i модулей вектора v_i скоростей молекул; k = 1,38·10^-23 Дж/K - постоянная Больцмана. Дано: φ; dφ; T; n_к; m/η_dφ =? η₀ =?

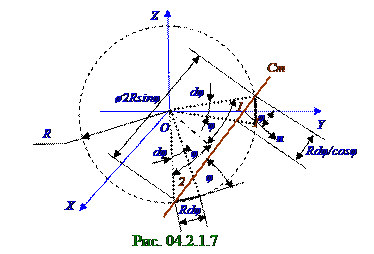
Направим OY ось вправо и Ст стенку расположим под φ углом к OY оси, вследствие чего схема задачи 04.2.1.9 примет вид на рис. 04.2.1.7.

Площадь dS кольца (рис. 04.2.1.7) шириной Rdφ/cosφ, образованного пересечением Ст стенки со сферой R = 1 ед. радиусом и имеющей φ угол n нормали к поверхности Ст стенки с OY осью, имеет следующий вид: dS = 2πR²sinφdφ/cosφ.(9.1)

Телесный угол dΩ - это площадь сферы, которую "вырезают" R = 1 ед. радиусы, между которыми dφ угол, имеет с учётом (9.1) следующий вид: dΩ = dScosφ = 2πsinφdφ.(9.2)

f(v_Y)=(m/2πkT)^1/2exp(-m v_Y ²/2kT) - плотность вероятности проекций v_iY на Ov_Y ось v_i вектора скоростей молекул.

Количество dη_dφ столкновений в единицу времени на единицу площади ( 9.4) dN молекул, векторы v_i скоростей которых направлены по OY оси c величиной проекций v_iY на Ov_Y ось

в диапазоне v_{iY …} v_{iY +} dv_i значений, имеет следующий вид:

dη_dφ= n_кΩ₀ f(v_Y)cosφ v_Ydv_Y = n_к(sinφcosφdφ/2)(m/2πkT)^1/2exp(- mv_Y ²/2kT)v_Ydv_Y,( 9.5)

где cosφ учитывает (рис. 04.2.1.7) возрастание площади, о которую ударяются молекулы, в 1/cosφ раз, поэтому количество ударов молекул в единицу времени на единицу площади уменьшается в cosφ раз.

Общее количество η_dφ столкновений в единицу времени на единицу площади ( 9.4) N молекул, векторы v_i скоростей которых направлены по OY оси c величиной проекций v_iY на Ov_Y ось

в диапазоне 0 _… ∞ значений, имеет с учётом (9.5) следующий вид:

v_Y2 → ∞ ∞

η_dφ= ∫dη_dφ= n_к(sinφcosφdφ/2)(m/2πkT)^1/2∫exp(- mv_Y ²/2kT)v_Ydv_Y = n_к(kT/8πm)^1/2(sinφcosφdφ),( 9.6)

v_Y1 = 0 0

∞

где ∫exp(- mv_Y ²/2kT)v_Ydv_Y рассчитан с помощью подстановки: mv_Y ²/2kT = z ↔ v_Y = (2kT/m)^1/2(z)^1/2 ↔

0 ∞

↔ dv_Y = (2kT/m)^1/2(1/2) (z) ^-1/2 ↔ z₁ = 0; z₂ → ∞ ↔(2kT/m)^1/2(2kT/m)^1/2(1/2) ∫exp(-z)(z)^1/2(z) ^-1/2dz = kT/m.

0

Под углами (рис. 04.2.1.6), значения которых находятся в φ… φ + dφ диапазоне, ударяются о

Ст стенку одновременно молекулы, находящиеся с четырёх сторон, две 1, 2 из которых изображены рис. 04.2.1.7, а две другие находятся в плоскости, перпендикулярной Ст стенке и OYZ плоскости. Поэтому η_dφ0 общее количество молекул, падающих в единицу времени на единицу площади под

φ… φ + dφ углами (рис. 04.2.1.6) относительно n нормали к поверхности Ст стенки, имеет с учётом

(9. 6) следующий вид: η_dφ0 = 4η_dφ= 4n_к(kT/8πm)^1/2(sinφcosφdφ) = n_к(2kT/πm)^1/2(sinφcosφdφ).( 9.7)

Количество η₀ соударений всех молекул (рис. 04.2.1.6) в единицу времени на единицу площади о Ст стенку, имеющих углы падения относительно n нормали к поверхности Ст стенки в диапазоне

0 _… π/2 значений, т.е. всех молекул, падающих в единицу времени на единицу площади под всеми возможными углами, имеет с учётом (9. 7) следующий вид:

φ₂ = π/2 π/2

η₀ = ∫η_dφ0 = n_к(2kT/πm)^1/2 ∫ sinφcosφdφ = (n_к/2)(2kT/πm)^1/2 = (n_к/4)(8kT/πm)^1/2= (n_к/4)<v>,( 9.6)

φ₁ = 0 0

где <v> = (8kT/πm)^1/2 - среднее арифметическое значение v_i модулей вектора v_i скоростей молекул (4.268) из раздела 04.2.0 "Физическая термодинамика".