Поляризация диэлектриков в электростатическом поле. Свободные, поляризационные заряды в диэлектрике 1 страница

Если полярныйдиэлектрик не находится во внешнем электростатическомполе с вектором

E напряжённостиэтого электростатического поля, то в результате теплового движения молекул векторы p_ei дипольных (5.61) электрических моментов этих молекул ориентированы хаотически. Поэтому суммавекторов p_ei дипольных электрических моментов всех молекул, содержащихся в любом макроскопическималом ΔV объёме диэлектрика, равна нулю. При внесении диэлектрикаво внешнее электростатическоеполе происходит поляризация диэлектрика, состоящая в том, что в любом малом его ΔV объёмевозникает отличный от нуля суммарныйвектор P дипольныхэлектрических моментов молекул.

Вектором P поляризованностиили векторомполяризациидиэлектрика называется отношение суммывекторов p_ei дипольных электрических моментов всех N молекул, находящихся в малом ΔV объёме диэлектрика, к величине этого ΔV объёма, т.е. вектор P поляризованности диэлектрика равен следующей сумме векторов p_ei дипольных электрических моментов всех молекул, содержащихся в единицеобъёма этого диэлектрика: N P = (1/ΔV) ∑p_ei, (5.69) i = 1

где p_ei - вектор(5.61) дипольного электрического момента i-ой молекулы, а N - общее число молекул в малом ΔV объёме. Этот ΔV объёмдолжен быть столь малым, чтобы в его пределах электростатическоеполес вектором E напряжённостиэлектростатического поля можно было считать однородным.

При модуле E вектора E напряжённостиэлектростатического поля в диэлектрике, имеющего значение E << kT/p_ei, где (4.28) из раздела 4.1 "Физическая термодинамика"k - постоянная Больцмана; (4.13) из раздела 4.1 "Физическая термодинамика" T - термодинамическаятемпература; p_ei - модуль (5.61) вектора p_ei дипольного электрического момент i-ой молекулы в диэлектрике, вектор P поляризованности неполярногои полярногодиэлектриков имеет следующий вид: P = ε₀χE, (5.70)

где χ - диэлектрическая восприимчивостьвещества.

Неполярнымидиэлектриками, например: H₂, N₂, O₂, CCl₂ называются такие, у которых в отсутствие внешнего электростатического поля"центры тяжести" положительного и отрицательного зарядов совпадают. У полярныхдиэлектриков, например: H₂O, HCl, NH₃, CH₃Cl электроны расположены несимметрично относительно атомных ядер. В таких молекулах "центры тяжести"положительных и отрицательных зарядов не совпадают даже в отсутствие внешнего электростатического поля.

У изотропногодиэлектрика χ относительная диэлектрическаявосприимчивостьвещества величина скалярная, так что вектор P поляризованностисовпадает по направлению свектором E электрическогополя. В (рис.5.14) результате поляризации диэлектрика в тонких слоях у ограничивающих от окружающего пространства его поверхностей S₁ и S₂ площадью, представляющего собой вакуум, возникают нескомпенсированные связанныезаряды, называемые поверхностными поляризационнымизарядами. У поверхности S₁ площадью, в которую входят силовые линиивектораE напряжённости электрическогополя, возникает избытокотрицательных зарядов молекул вследствие ориентации

вектора E напряжённостимолекул свекторомP поляризованности электрическогополя, возникает избыток отрицательных зарядов молекул, вследствие ориентации диполейпо направлению вектораE напряжённости электрическогополя. У противоположной поверхности S₂ площадью существует избыток положительныхзарядов. Согласнозакону сохранения электрического заряда алгебраическая сумма электрических зарядовтел или частиц, образующих электрически изолированнуюсистему не изменяется при любых процессах, происходящих в этой системе, поэтому в диэлектрике количество положительныхзарядовравноколичеству отрицательныхзарядов и в целом диэлектрик электронейтрален.

Связь поляризованности диэлектрика в электростатическом поле с плотностью поляризационных зарядов

В диэлектрике (рис. 5.15)толщиной d, находящегося в вакууме, выделен воображаемый косойцилиндр, ось которого совпадает с направлением вектора E напряжённости внешнего электрическогополя, с l длиной боковой поверхности, ΔS площадью основания и следующим ΔV объёмом: ΔV = lΔScosα,(5.71) где ΔScosα - проекция ΔS площади основания на плоскость, перпендикулярную направлению вектора E напряжённости внешнего электрическогополя.

Модуль P₀ вектора P₀ дипольного электрического момента всех молекул N количеством, находящихся в (5.71) ΔV объёме, с учётом модуля (5.69)дипольногоP электрического момента всех молекул, содержащихся в единицеобъёма этого диэлектрика, имеет следующий вид:

P₀ = PΔV = PlΔScosα. (5.72)

ПоложительныйΔq_p+ поляризационныйзаряд на правомоснованиикосогоцилиндра

ΔS площадью равен по величине и противоположен по знаку отрицательномуΔq_p- поляризационному заряду на левомоснованиикосогоцилиндра той же ΔS площади. С учётом σ_p поверхностной плотности связанныхзарядов на правой и левой поверхностях диэлектрикавеличина Δq_pполяризационного заряда на ΔS площади имеет следующийвид: Δq_p = σ_pΔS. (5.73) Модуль P₀ вектора P₀дипольного(5.61)электрического момента противоположных по знаку зарядов Δq_p- и Δq_p+ с учётом l расстояния между ними и (5.73) имеет следующийвид: P₀ = Δq_pl = σ_pΔSl. (5.74)

Приравниваем (5.72) и (5.74) и получаем следующее выражение:

PlΔScosα = σ_pΔSl ↔ Pcosα = σ_p ↔ σ_p = P_n, (5.75) где P_n - проекцияна внешнюю nнормаль к поверхности диэлектрика вектора P поляризованности, на которой определяют σ_p поверхностнуюплотностьполяризационныхзарядов.

Для правой поверхности диэлектрика(рис. 5.15) внешняя n₂нормаль направлена в одну сторону свекторомP поляризованности, поэтому проекция P_n на внешнюю n₂нормаль к поверхности диэлектрика вектора P поляризованности положительна, т.е. P_n > 0, и вследствие этогоповерхностнаяплотность σ_p+ поляризационныхзарядовна правой поверхности диэлектрика положительная.

На левой поверхности диэлектрика(рис.5.15) внешняя n₁нормаль направлена в противоположную сторону относительновектораP поляризованности, поэтому проекция P_n на внешнюю n₁нормаль к поверхности диэлектрика вектора P поляризованности отрицательна, т.е. P_n < 0, и вследствие этого σ_p- поверхностнаяплотность поляризационныхзарядовна этой поверхности отрицательная.

поверхности ΔS площадью, равно N/2 количествумолекул, находящихся слева от поверхности ΔS площадью.

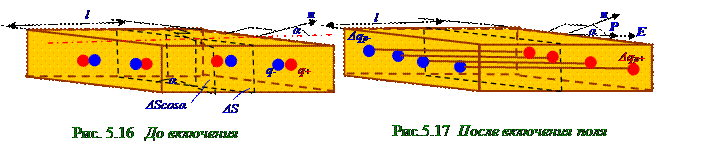
После включения (рис.5.17) внешнего электрическогополясвектором E напряжённостиэтогоэлектрическогополя через делящую призму пополам поверхности ΔS площадью в левуюего часть проходят N/2 количествоотрицательныхзарядов, а в правуюего часть проходят N/2 количествоположительныхзарядов. Таким образом, после включения (рис.5.17) внешнего электрическогополясвектором E напряжённостиэтогоэлектрическогополя через делящую призму пополам поверхность ΔS площадью проходит Δq_p заряд всех (5.76) N количеством молекул, который имеет с учётом равенства q₊ = | q_- | = q модулей q₊ положительногои q_- отрицательногоq_- заряда следующеезначение: Δq_p = qN = qnlΔScosα, (5.77) в результате чего неполярныемолекулы поляризуютсяс образованием слеваи справаот поверхности ΔS площадью соответственно Δq_p-отрицательногои Δq_p+ положительного связанногозарядов.

Векторыp_e (5.61) дипольныхэлектрических моментов каждой молекулы, находящихся

(рис.5.16) в ΔV = lΔScosα объёме, ориентированы по внешнему электрическомуполюс векторомE напряжённостиэтогоэлектрическогополя, поэтому (5.69) модуль P вектора P дипольногоэлектрического момента, т.е. сумма модулей p_ei векторов p_ei дипольных электрических моментов всех молекул, находящихся в единицеобъёма диэлектрика, имеет следующий вид: P = p_ein = qnl, (5.78)

где n - концентрация молекул в диэлектрике; p_ei - модуль вектора p_ei дипольного электрического момента i-ой молекулы в диэлектрике, имеющего (5.61) выражение: p_ei = ql.

Подставляем (5.78) в (5.77) и получаем выражение для расчёта величины Δq_p-= - Δq_p связанного отрицательн огозаряда на (рис.5.17) левой поверхности ΔS площадью диэлектрика, а также получаем следующее выражения для расчёта величины Δq_p+ = Δq_pсвязанного положительногозаряда на (рис.5.17) правойповерхности ΔS площадью диэлектрикапри условии нахождениядиэлектрикавовнешнем электрическомполес векторомE напряжённостиэтогоэлектрическогополя: Δq_p = qnlΔScosα ↔ Δq_p = PΔScosα = PnΔS, (5.79) где n - нормаль(рис.5.17) к поверхности ΔS площадью диэлектрика; P - вектор поляризованности диэлектрика и α - угол между n и P.

Теорема Гаусса в интегральной форме для вектора поляризованности диэлектрика, находящегося в электростатическом поле

Положительный (рис.5.18) свободныйq₊ заряд создаёт в диэлектрике сферическое векторное электростатическогополе с направлением векторов E напряжённостиэтогоэлектростатическогополя по радиусу от охватываемого воображаемой сферой S площадьюположительного свободногоq₊ заряда.

Вследствие этого молекулы диэлектрика поляризуютсяи их векторы P поляризованности ориентируются по силовым линиямвектора E напряжённости электростатическогополя, направление которых совпадает с направлением внешней n нормали квоображаемой сфере

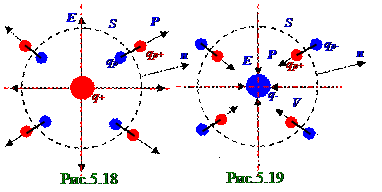
воображаемой сферы S площадью. Поляризациямолекул диэлектрика на рис.5.19 аналогична

рис. 05.0.18 с отличием в направлении вектора E напряжённости электростатическогополя. Поэтому для расчёта Δq_p связанногозаряда, прошедшего (рис.5.18), (рис.5.19) через поверхность ΔS площадью воображаемой сферы S площадью при поляризациямолекул диэлектрика можно использовать (5.79) выражение.

Перейдём в (5.79) от приращенийк дифференциалами получим следующее выражение для расчёта элементарного dq_p связанногозаряда, прошедшего (рис.5.18), (рис.5.19) через элементарную поверхность dS площадью воображаемой сферы S площадью при поляризациямолекул диэлектрика: Δq_p = PnΔS ↔ dq_p = PndS = PdS. (5.80) Через всю воображаемую сферу S площадью при поляризации диэлектрика пройдет связанныйq_p заряд, в результате чего в объёме (рис.5.18), ограниченном воображаемой сферой

S площадью, охватывающейсвободныйq₊ заряд, возникает q_p- отрицательный поляризационныйзаряд, который определяется следующим интегрированием элементарного (5.80) dq_p связанногозаряда по замкнутойповерхности,которой являетсявоображаемая сфера S площадью:

q_p- = - ∫ dq_p = - ∫PdS =-Ф_p, (5.81) (S) (S)

где Ф_p - поток вектора P поляризованности диэлектрикачерез воображаемую сферу S площадью. Отрицательный (рис.5.19) свободныйq_- заряд создаёт в диэлектрике сферическое векторное электростатическогополе с направлением векторов E напряжённостиэтогоэлектростатическогополя, направленного по радиусу к воображаемой сфере S площадью к охватываемому этойвоображаемой сферой S площадью q_-отрицательного свободногозаряда.

Вследствие этого, молекулы диэлектрика поляризуютсяи их векторы P поляризованности диэлектрика ориентируются по силовым линиямвектора E напряжённости электростатическогополя, направление которых противоположно направлению внешней n нормали квоображаемой сфере S площадью, охватывающей q_- отрицательный (рис.5.19) свободныйзаряд.

В объёме V (рис.5.19) образуется q_p+ положительный поляризационный заряд, т.к. PdSскалярноепроизведение в (5.81) отрицательно.

Выражение (5.81) является математической формулировкой в интегральной форме теоремы Гаусса для вектора P поляризованности диэлектрика.

Теорема Гаусса в дифференциальной форме для вектора поляризованности диэлектрика, находящегося в электростатическом поле

Введём (5.10) объёмнуюρ_pплотность q_pполяризационныхзарядов в V объёме диэлектрика, ограниченном замкнутой воображаемой поверхностью S площадью. Тогда с учётом выражения (5.81)для q_pполяризационного заряда, определения (5.10) объёмнойρ плотности свободных зарядов и по аналогии с (5.21), где согласно теореме Остроградского - Гаусса поверхностныйинтегралпозамкнутойповерхности S площадью заменён объёмныминтегралом по V объёму диэлектрика, ограниченному этой замкнутойповерхностью S площадью, выражение для определения ρ_pобъёмной плотностиполяризационногоq_p зарядав рассматриваемом V объёме диэлектрика имеет следующий вид: q_p = ∫ ρ_pdV = - ∫PdS= - ∫ PdV ↔ ρ_p = - P = - divP,(5.82) V (S) V

где знак q_pполяризационногозаряда и его ρ_p объёмной плотностиопределяется знаком

PdSскалярногопроизведения.

Если вектор P поляризованности диэлектрика совпадает (рис. 05.0.18) по направлению с внешней n нормалью квоображаемой поверхности S площадью, охватывающей q_p- отрицательный связанныйзаряд, то q_p- < 0 и ρ_p- < 0.

Если вектор P поляризованности противоположен по направлению внешней n нормали квоображаемой поверхности S площадью, охватывающей q_p+ положительныйсвязанный заряд, то q_p+ > 0 и ρ_p+ > 0.

Согласно (5.82) объёмнаяρ_pплотность связанныхзарядов, находящихся в рассматриваемой точке объёма диэлектрика равна дивергенции(div) от вектора P поляризованности диэлектрика, взятой с отрицательным знаком.

Дивергенция(div) от вектора P поляризованности диэлектрика в прямоугольной декартовой системе(1.1) из раздела 1.0 "Физические основы механики" координат имеет следующий вид: ρ_p = - P = - divP= - [(∂P_X/∂x) + (∂P_Y/∂y) + (∂P_Z/∂z)]. (5.83)Выражение (5.83) - это математическое выражение в дифференциальнойформе теоремы Гаусса для вектора P поляризованности диэлектрика, которая имеет следующую формулировку: дивергенцияdiv P вектораP поляризованности диэлектрикав электростатическом поле, которое обозначается также P, численно равенприращениюпроекций P_X; P_Y и P_Y на оси

OX, OY и OZ координат вектора P поляризованности диэлектрика на единицедлиныкаждой из координат в рассматриваемой точке некоторого объёма. Этоприращениепроекций P_X; P_Y и P_Y на оси OX, OY и OZ координат вектора P поляризованности диэлектрика пропорциональноρ_p объёмной плотности связанногозаряда, находящегося в рассматриваемой точке объёма диэлектрика.

Если поляризационныйзаряд имеет ρ_p- отрицательную объёмную плотность, т. е. ρ_p- < 0 и (5.83) divP >0, то вектор P поляризованностидиэлектрика совпадает по направлению с внешней

n нормалью(рис.5.18) квоображаемой поверхности S площадью и поэтому отрицательный поляризационныйзаряд q_p- является источником вектора P поляризованностидиэлектрика. Если поляризационный заряд имеет ρ_p+ положительную объёмную плотность, т. е. ρ_p+ > 0 и (5.81) divP <0, то вектор P поляризованностидиэлектрика противоположен по направлению с внешней n нормалью (рис.5.19) квоображаемой поверхности S площадью и поэтому

q_p+ положительный поляризационныйзаряд является стоком вектора P поляризованностидиэлектрика.

Вектор электрического смещения в диэлектрике

Поляризационные q_pзаряды отличаются от q свободных, т.е. стороннихзарядов тем, что поляризационныеq_pзаряды не могут покинуть пределы молекул, в состав которых они входят. Они служат источником электрическогополя, поэтому согласно (5.21) теореме Гаусса в дифференциальнойформе к ρ объёмнойплотности свободных зарядов следует добавить ρ_pобъёмную плотность поляризационныхзарядов, вследствие чего дифференциальнаяформа теоремы Гауссапринимаетследующий вид: E = (ρ + ρ_p)/ε₀.(5.84) Подставляем выражение(5.83) связи ρ_pобъёмной плотность связанныхзарядов с дивергенцией(div) от вектора P поляризованности диэлектрика в рассматриваемой точке объёма диэлектрика в (5.84) и получим следующее выражение, связывающее ρобъёмнуюплотность свободных зарядов с дивергенцией(div) от суммы векторовε₀E напряжённостиэлектростатического поля и P поляризованности диэлектрика в этой рассматриваемой точке объёма диэлектрика: E = (ρ - P)/ ε₀ ↔ ε₀ E + P = ρ ↔ (ε₀E + P)= ρ. (5.85) Выражение: ε₀E + P = D (5.86) назвали вектором D электрического смещенияили электрической индукцией. С учётом (5.70)

P = ε₀χE, где χ - относительная диэлектрическая восприимчивостьвещества, выражение (5.86) принимает следующий вид: D = ε₀E + ε₀χE = ε₀(1 +χ)E = ε₀εE, (5.87) где ε = 1 + χ - диэлектрическаяпроницаемость среды; E - векторнапряжённостиэлектростатического поля в рассматриваемой точке объёма диэлектрика, где относительная диэлектрическаяпроницаемость равна ε. В вакуумеχ = 0 и ε = 1.

Теорема Гаусса для электростатического поля в диэлектрике в дифференциальной и интегральной формах

Из (5.85) и (5.86) получаем следующее выражение, связывающее ρобъёмнуюплотность свободных зарядов с дивергенцией(div) вектора D электрического смещенияв рассматриваемой точке объёма диэлектрика: D= ρ, (5.88)

которое является математическим выражением теоремы Гаусса для электростатического поля в дифференциальнойформе в диэлектрике.

Далее согласно (5.21) теореме Остроградского - Гауссаперехода от объёмногоинтеграла по

V объёму диэлектрика, в котором распределены(5.10) с ρ объёмнойплотностью свободные заряды, к поверхностномуинтегралупозамкнутойповерхности S площадью, которая охватывает этот V объём диэлектрика, с использованием (5.88) получаем следующее выражение теоремы Гаусса для электростатического поля в интегральнойформе в диэлектрике:

D = ρ ↔ ∫ DdV = ∫ ρdV ↔ ∫ DdS= ∫ ρdV↔ N_D= ∫ ρdV = ∑q_i, (5.89) V V (S) V V i = 1

где по аналогии (5.17) с N_E потоком вектора E напряженностив вакууме электростатическогополя через замкнутую воображаемуюповерхность S площадью N_D - это поток вектора D электрического смещения через замкнутую поверхность S площадью, охватывающую V объём диэлектрика, в котором распределеныс ρ объёмной плотностью свободные заряды.

Согласно (5.89) N_D потоквектора D электрического смещения через замкнутую поверхность S площадью равен всему q свободному заряду, распределённому с ρ объёмнойплотностью в V объёме при непрерывномраспределении заряда или алгебраическойсумме заключённых внутри V объёма и ограниченных замкнутой воображаемойповерхностью S площадьюсвободныхq_iдискретныхзарядов.