Cвободные, т.е.нескомпенсированные,заряды равномерно распределены с объёмной
ρ плотностью по шару R радиуса, находящегося в вакууме и изготовленного из однородного изотропного диэлектрического материала с относительной ε диэлектрической проницаемостью. Определить: а) зависимость модуля E(r) вектораE напряжённостиэлектрическогополя, φ(r) потенциала в шаре и за его пределами в функции r расстояния от центра этого шара; изобразить примерные графики зависимостей E(r), φ(r); б) зависимость ρp(r) объёмной,σp(r) поверхностнойплотностиполяризационныхзарядов в шаре в функции r расстояния от центра этого шара.
Дано: R; ρ; ε /E(r) = ? φ(r) = ? ρp(r) = ? σp(r) = ?
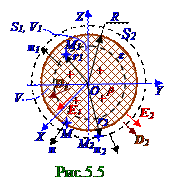
Электростатическое поле, создаваемое (рис. 5.5) шаром R радиуса, находящегося в вакууме и выполненного из однородного изотропного диэлектрического материала с относительной
ε диэлектрической проницаемостью будетвнутри, т.е. при r1 ≤ R, и вне, т.е. при r1 ≥R,этого шарасферическимвекторным полем. Векторы (рис.5.5) E напряженности(5.3) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля" D = ε0εE электрического смещения(5.87) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля "в этом электростатическом поле проходит через центр сферы, а проекции Er, Dr на направление
r радиуса - вектора векторов соответственноE напряжённости, D электрического смещенияэтого электростатическогополя, являющееся сферическимвекторным полем, является функцией r расстояния от центра сферы. Поток NDвектора D электрического смещения через воображаемую сферическую(рис.5.2.5) поверхность S1 площадью, согласно (5.118) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля "имеет следующий вид: N1D = ∫D1dS= ∫D1ndS = ∫D1rdS = D1r4πr12, (3.1) (S1) (S1) (S1)
|
Согласно (5.89) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля" теореме Гаусса для электростатического поля в интегральнойформе в диэлектрике ND поток вектора D электрического смещения через воображаемую сферическую(рис.5.5) поверхность S2 площадью, охватывающую V1 объём диэлектрика, в котором распределеныс, например, с положительной ρ объёмной плотностью свободные, т.е.нескомпенсированные,заряды имеет следующий вид:
N1D = ∫ρdV = ρ(4/3)πr13, (3.2) V1
где V1 = (4/3)πr13 - объём диэлектрика в шаре, ограниченном воображаемой сферическойповерхностью S1 площадьюи r1 ≤ R радиусом.
Приравниваем (3.1) и (3.2), после чего получаем следующее выражение D1r проекции на направление r1 радиуса - вектора вектора D1 электрического смещенияв произвольной M1 точке пространствадиэлектрической среды внутри шара, т.е. при r1 ≤ R:
D1r4πr12 = ρ(4/3)πr13↔ D1r = ρr1/3. (3.3)
С учётом(5.87) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля " связи D1 = ε0εE1 вектора D1 электрического смещенияс вектором E1 напряжённости электростатическогополяE1r проекция на направление r1 радиуса - вектора E1 векторанапряжённостиэтого электростатическогополя в произвольной M1 точке пространствадиэлектрической среды внутри шара, т.е. при r1 ≤ R, имеет следующий вид: E1r = D1r/ε0ε = ρr1/3ε0ε, (3.4) где ε - относительная диэлектрическаяпроницаемость однородного изотропного материала,из которого изготовлен шар.
Поток N2D вектора D2 электрического смещения через воображаемую сферическую
(рис. 5.2.5) поверхность S2 площадью, проведённую в вакуумевокруг шара,согласно (5.118) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля ",имеет следующий вид:
N2D = ∫D2dS= ∫D2ndS = ∫D2rdS = D2r4πr22, (3.5) (S2) (S2) (S2)
где S2 = 4πr22 - площадь воображаемой сферической поверхности, проведённой в вакуумевокруг шара, r2 ≥ R радиусом с центром, совпадающим с O центром диэлектрического шара; D2n - проекция на направление внешней n2 нормали к воображаемой сферическойповерхность S2 площадью, проведённую в вакуумевокруг шара,вектора D2 электрического смещения совпадает с
D2r проекцией на направление r2 радиуса - вектора этого вектора D2 электрического смещенияв произвольной M2 точке пространствадиэлектрической среды вне шара, т.е. при r2 ≥ R.
Согласно (5.89) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля "теореме Гаусса для электростатического поля в интегральнойформе в диэлектрике N2D поток вектора D2 электрического смещения через воображаемую сферическую(рис. 05.2.5) поверхность S2 площадью, проведённую в вакуумевокруг шара и охватывающую V объём диэлектрика, т.е. охватывающую весь шарR радиусом, в котором распределеныс ρ объёмной плотностью свободныеилинескомпенсированныезаряды, имеет следующий вид: N2D = ∫ρdV = ρ(4/3)πR 3, (3.6) V
где V = (4/3)πR3 - объём диэлектрического шара R радиусом.
Приравниваем (3.5) и (3.6), после чего получаем следующее выражение D2r проекции на направление r2 радиуса - вектора вектора D2 электрического смещенияв произвольной M2 точке пространствав вакуумевне шара, т.е. при r2 ≥ R: D2r4πr22 = ρ(4/3)πR3 ↔ D2r = ρR3/3r22. (3.7)
С учётом(5.87) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля" связи D2 = ε0E2 вектора D2 электрического смещенияс вектором E2 напряжённости электростатическогополяE2r проекция на направление
r2 радиуса - вектора E2 векторанапряжённостиэтого электростатическогополя в произвольной
M2 точке пространствав вакуумевне шара, т.е. при r2 ≥ R, имеет следующий вид: E2r = D2r/ε0 = ρR3/3r22ε0. (3.8)
Согласно (5.117) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля"φ1потенциал (рис.5.2.5) в произвольной
M1 точке пространствадиэлектрической среды внутри шара с учётом (3.4) E1r проекции на направление r1 радиуса - вектора E1 векторанапряжённости электростатическогополя в произвольной M1 точке пространствадиэлектрической среды внутри шара, т.е. при r1 ≤ R, а также с учётом (3.8) E2r проекции на направление r2 радиуса - вектора E2 векторанапряжённостиэтого электростатическогополя в произвольной M2 точке пространствав вакуумевне шара, т.е. при r2 ≥ R, имеет следующий вид: R ∞ R ∞
φ1 = ∫E1rdr + ∫E2rdr = ∫(ρr/3ε0ε)dr + ∫(ρR3/3r2ε0 )dr= (ρ/6ε0ε)[R2 - r12] + (ρR2/3ε0 ),(3.9) r1 R r1 R
где r1 ≤ R.
Согласно (5.117) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля"φ2потенциал (рис.5.2.5) в произвольной M2 точке пространствав вакуумевне шара с учётом (3.8) E2r проекции на направление r2 радиуса - вектора E2 векторанапряжённости электростатическогополя в произвольной M2 точке пространствав вакуумевне шара, т.е. при r2 ≥ R, имеет следующий вид:
∞ ∞ φ2 = ∫E2rdr = ∫(ρR3/3r2ε0 )dr = ρR3/3ε0r2,(3.10) r2 r2
где r2 ≥ R.
Согласно (5.94) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля"при переходе через границу диэлектриков с различными ε1 и ε2 относительными диэлектрическимипроницаемостями при равенстве нулю поверхностнойσ плотности свободных, т.е.нескомпенсированных, зарядов на этой границе диэлектриковнормальная Enсоставляющая вектора E напряжённости электростатическогополя претерпевает разрыв.
На границе (рис.5.5) шара, изготовленного из однородного изотропного диэлектрического материала с относительной ε1 > 1 диэлектрической проницаемостью, с вакуумом, где относительная диэлектрическаяпроницаемость равна единице, т.е. ε2 = 1, проекция En на направление внешней
n нормали к поверхности сферы S площадьювектора Eнапряжённости электростатическогополя совпадает с Er проекцией на направление r радиуса - вектора этого вектора Eнапряжённости электростатическогополяв произвольной M точке на поверхности сферы S площадью. Вследствие чего отношение E1r проекции на направление r1 радиуса - вектора E1 векторанапряжённости электростатическогополясо стороны диэлектрического шара к E2r проекции на направление
r2 радиуса - вектора E2 векторанапряжённостиэтого электростатическогополя в произвольной
M точке на поверхности сферыS площадью со стороны вакуумаимеет следующий вид:
E1r/E2r = ε2/ε1 ↔ E1r/E2r =1/ε1, (3.11)
где ε2 = 1 относительная диэлектрическаяпроницаемость вакуума.
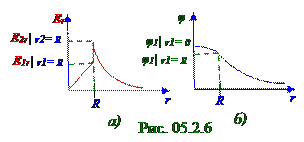
Согласно (3.11)нормальная Enсоставляющая E векторанапряжённости электростатическогона границе (рис.5.2.5) диэлектрического шара с вакуумом претерпевает разрыв, что отражено на рис. 5.6, а скачком графическойзависимости от значения E1r| r1= R проекции на направление
r2 радиуса - вектора E1 векторанапряжённости электростатическогополя со стороны диэлектрического шара до значения E2r| r2= R проекции на направление r2 радиуса - вектора E2 векторанапряжённостиэтого электростатическогополя в произвольной M точке на поверхности сферы
S площадью со стороны вакуума.
Согласно (3.9), (3.10) φ1потенциал (рис.5.6, б) в диэлектрической среде внутри шара монотонноуменьшается от максимальногозначения в O центре диэлектрического шара до значения
φ = ρR2/3ε0 на поверхности этогошара и дальше уменьшатся до нуля при r → ∞.
|
совпадает по направлению свектором E напряжённости электрическогополя в этом диэлектрике, вследствие чего имеет место следующее выражение: P = ε0χE = ε0(ε - 1)E,(3.12)
где χ = (ε - 1) - где χ относительная диэлектрическаявосприимчивостьвещества связана согласно (5.87) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля "cε относительной диэлектрическойпроницаемостью этого вещества.
Согласно (5.75)из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля " σp поверхностнаяплотностьполяризационныхзарядов (рис. 05.2.5) шара, находящегося в вакууме и выполненного из однородного изотропного диэлектрического материала с относительной ε диэлектрической проницаемостью,равна следующей Pn проекциина внешнюю nнормаль к поверхности диэлектрикавектора P поляризованностив этом диэлектрике:
σp = Pn = Pcos(P^n)=ε0(ε - 1) E1rcos(E ^n) = ε0(ε - 1)E1r, (3.13)
где (P^n) =(E ^n) = 90° - угол между вектором P поляризованностиили согласно (3.14)между вектором E электрическогополя и внешней nнормалью к поверхности диэлектрика;
P=ε0(ε - 1)E - модуль вектора P поляризованностидиэлектрика.
Подставляем проекцию E1r (3.4) на направление r1 радиуса - вектора E1 векторанапряжённости электростатическогополя в (рис.5.2.5) произвольной M точке на поверхности сферы S площадьюсо стороны диэлектрического шара, т.е. при r1 = R, в (3.13) и получаем следующее выражение
σp поверхностнойплотностиположительных поляризационныхзарядов шара, которыйимеет равномерно распределенный по объёму шара R радиуса свободные, т.е.нескомпенсированные,заряды ρ плотностью по шару R радиуса, который находится в вакууме и который выполнен из однородного изотропного диэлектрического материала с относительной ε диэлектрической проницаемостью: σp = ε0(ε - 1)E1r = ρRε0(ε - 1)/3ε0ε= ρR (ε - 1)/3ε. (3.14)Объёмное(5.83) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля" распределение ρpплотности отрицательных поляризационных зарядовс учётом того, что векторы P поляризованности внутри диэлектрического шараобразуют сферическоевекторное поле с (3.13) P1r проекциейна направление
r1 радиуса - вектора диэлектрического шара вектора P поляризованности,имеет следующий вид: ρp = - divP= - (1/r)∂(rP1r)/∂r = - (1/r2)∂(r2ε0(ε - 1)E1r)/∂r = - (1/r2)∂[r2ε0(ε - 1)ρr/3ε0ε]/∂r =
= - (ε0(ε - 1)ρ/3ε0ε)(1/r2)3r2 = - (ε - 1)ρ/ε. (3.15) Полный qpρ отрицательныйполяризационный заряд (рис. 05.2.5) в объёме диэлектрика шара с R радиусом с учётом (3.16) постоянного значения ρpплотности отрицательных поляризационных зарядов по объёму V = (4/3)πR3 этогошара имеет следующее значение:
qpρ = ρp V = - [(ε - 1)ρ/ε] (4/3)πR3 = - 4(ε - 1)ρπR3/3ε. (3.16)
Полный положительный qpσ поляризационный заряд (рис. 05.2.5) на поверхности диэлектрического шараR радиусом с учётом (3.14) постоянного значения σp поверхностнойплотностиположительных поляризационныхзарядов на поверхности S = 4πR2 площадью этогошара имеет следующее значение: qpσ = σpS = [ρR (ε - 1)/3ε]4πR2 = 4(ε - 1)ρπR3/3ε. (3.17)Диэлектрик(рис. 5.2.5), из которого изготовлен шар с R радиусом до введения в него например, с положительной ρ объёмной плотностью свободных, т.е.нескомпенсированных,зарядов был электронейтрален. Согласно параграфу "Поляризация диэлектриков в электростатическом поле. Свободные заряды, связанные заряды в поляризованном диэлектрике"из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля"закону сохранения электрического заряда алгебраическая сумма электрических зарядовтел или частиц, образующих электрически изолированнуюсистему не изменяется при любых процессах, происходящих в этой системе, вследствие чего после введения в диэлектрик, например, с положительной ρ объёмной плотностью свободных, т.е.нескомпенсированных,зарядов он должен остаться электронейтральным. Это означает равенство нулюq∑ суммарного поляризационного заряда после введения в диэлектрик, например, с положительной ρ объёмной плотностью свободных, т.е.нескомпенсированных,зарядов, т.е. равенство нулю суммыполного (3.16) отрицательного qpρполяризационного заряда в объёме диэлектрикас полным (3.17)положительным qpσ поляризационным зарядом на поверхности диэлектрикогошара, т.е. выполнения следующего равенства:
q∑ = qpρ + qpσ = [4(ε - 1)ρπR3/3ε] - [4(ε - 1)ρπR3/3ε] = 0. (3.18) Выполнение (3.18) равенства свидетельствует о правильностирасчёта.
Дата добавления: 2016-02-14; просмотров: 1591;
