ДИНАМИКА раВномерного ДВИЖЕНИЯ
ПО ОКРУЖНОСТИ
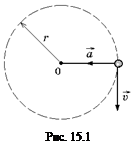 Пусть некоторое тело массой т движется по окружности радиуса r с постоянной по модулю скоростью υ (рис. 15.1). Вспомним, что угловая скорость
Пусть некоторое тело массой т движется по окружности радиуса r с постоянной по модулю скоростью υ (рис. 15.1). Вспомним, что угловая скорость 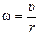 .
.
Как мы знаем, в данном случае ускорение тела  направлено к центру окружности и по модулю равно:
направлено к центру окружности и по модулю равно:
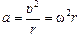 . (15.1)
. (15.1)
Это ускорение называется центростремительным. Но для того чтобы тело двигалось с центростремительным ускорением, согласно второму закону Ньютона необходимо, чтобы равнодействующая 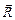 всех сил, действующих на тело, была направлена к центру окружности и равнялась по модулю:
всех сил, действующих на тело, была направлена к центру окружности и равнялась по модулю:
R = та = 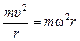 . (15.2)
. (15.2)
  а) б)
Рис. 15.2
а) б)
Рис. 15.2
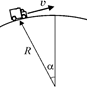
| Задача 15.1. Автомобиль массы т едет с постоянной скоростью υ по выпуклому мосту, радиус кривизны которого равен R (рис. 15.2). Найти силу нормальной реакции моста и силу трения, если радиус, проведенный в точку нахождения автомобиля составляет с вертикалью угол a. |
| т R υ a | Решение. На автомобиль действуют три силы: сила тяжести 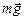 , сила нормальной реакции , сила нормальной реакции  и сила трения покоя со стороны дороги (рис. 15.2,б). Заметим, что если бы и сила трения покоя со стороны дороги (рис. 15.2,б). Заметим, что если бы  не толкала автомобиль вперед, уравновешивая тем самым касательную составляющую силы тяжести не толкала автомобиль вперед, уравновешивая тем самым касательную составляющую силы тяжести 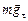 , то автомобиль не мог бы двигаться равномерно! , то автомобиль не мог бы двигаться равномерно!
|
| N = ? Fтр = ? | |
Введем систему координат пОt, запишем второй закон Ньютона в проекциях на оси 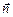 и
и 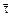 :
:
п: –N + mgcosa =  , (1)
, (1)
t: Fтр – mgsina = 0. (2)
Из (1) и (2) получаем ответ:  ; Fтр = mgsina.
; Fтр = mgsina.
СТОП! Решите самостоятельно: В1, В2, С1.
Задача 15.2. На дно сферы радиуса R насыпали горсть песка. Где будут находиться песчинки после того, как сфера будет приведена во вращение вокруг вертикальной оси с угловой скоростью w? Трение песчинок о сферу мало.
| R w | Решение.Пусть песчинки будут находиться в некоторой точке В (рис. 15.3). Тогда их положение можно считать заданным, если известен угол a, который образует радиус ОВ = R с вертикалью.
На песчинки действуют две силы: 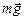 и и  . Под действием этих сил песчинки движутся по окружности радиусом r = Rsina с центром в точке О¢. . Под действием этих сил песчинки движутся по окружности радиусом r = Rsina с центром в точке О¢.
| 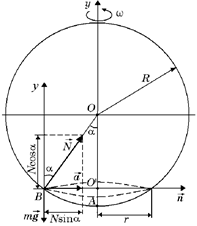 Рис. 15.3
Рис. 15.3
|
| a = ? | ||
Центростремительное ускорение  направлено к точке О¢ и равно а = wr2 = w2Rsina.
направлено к точке О¢ и равно а = wr2 = w2Rsina.
Запишем второй закон Ньютона в проекциях на оси 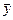 и
и 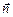 :
:

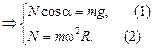
Разделив (1) на (2), получим  . Отсюда получаем ответ:
. Отсюда получаем ответ: 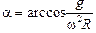 .
.
Читатель: Косинус любого угла не больше 1, но значение g/w2R может быть и больше 1. Что бы это значило?
Автор: Если g/w2R = 1, т.е. 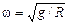 , то a = 0. Значит, все песчинки находятся в нижней точке сферы – точке А. То же самое произойдет и в случае g/w2R > 1, т.е. если
, то a = 0. Значит, все песчинки находятся в нижней точке сферы – точке А. То же самое произойдет и в случае g/w2R > 1, т.е. если  .
.
Читатель: Значит, если постепенно раскручивать сферу, то первое время все песчинки будут лежать в точке А, а как только w превысит значение 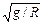 , они постепенно поползут вверх по стенке сферы?
, они постепенно поползут вверх по стенке сферы?
Автор: Да, но с небольшими оговорками: 1) песчинки должны лежат не точно в точке А, а чуть-чуть рядом, иначе они просто будут неподвижны и 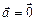 ; 2) если сфера абсолютно гладкая, то она не сможет увлечь в движение песчинки, т.е. сфера будет вращаться, а песчинки будут скользить по ней, оставаясь неподвижными относительно земли.
; 2) если сфера абсолютно гладкая, то она не сможет увлечь в движение песчинки, т.е. сфера будет вращаться, а песчинки будут скользить по ней, оставаясь неподвижными относительно земли.
СТОП! Решите самостоятельно: В4, С2, С3.
Задача 15.3. Два маленьких шарика массами т1 и т2, привязанные легкими нерастяжимыми нитями (рис. 15.4,а), вращаются в горизонтальной плоскости с угловой скоростью w вокруг вертикальной оси. Расстояния l1 и l2 заданы. Определите силы натяжения нитей. Силу тяжести не учитывать.
| т1, т2, l1, l2, w | Решение. На шарик т2 действует только одна нить с силой Т2, а на шарик т1 – две нити силами Т1 и Т2 соответственно. |
| Т1 = ? Т2 = ? |
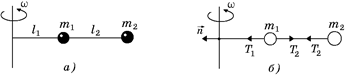
Рис. 15.4
Запишем второй закон Ньютона в проекции на ось 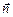 (рис. 15.4,б) для каждого шарика:
(рис. 15.4,б) для каждого шарика:
т1: Т1 – Т2 = тw2l1, (1)
т2: Т2 = тw2(l1 + l2), (2)
Подставляя (2) в (1), получим Т1 = тw2(2l1 + l2).
Ответ: Т1 = тw2(2l1 + l2); Т2 = тw2(l1 + l2).
СТОП! Решите самостоятельно: С5, С7, С9.
Задача 15.4. Конструкция на рис. 15.5,а вращается с постоянной угловой скоростью w вокруг вертикальной оси. Шарик скользит по стержню без трения, длина пружины в нерастянутом состоянии l0, угол a задан. Определите жесткость пружины, если из-за вращения пружина увеличила свою длину на Dl.
| w l0 a Dl |
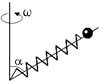 а)
Рис. 15.5
а)
Рис. 15.5
| 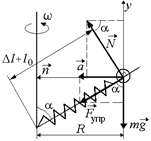 б)
б)
|
| k = ? | ||
Решение. На шарик действуют три силы: 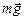 ,
,  ,
, 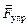 , причем
, причем 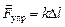 (рис. 15.5,б). Запишем второй закон Ньютона в проекции на оси
(рис. 15.5,б). Запишем второй закон Ньютона в проекции на оси 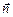 и
и 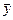 , учитывая, что шарик движется по окружности радиуса R = (l0 + Dl)sina:
, учитывая, что шарик движется по окружности радиуса R = (l0 + Dl)sina:
у: Nsina – kDlcosa – mg = 0,
n: Ncosa + kDlsina = mw2(l0 + Dl)sina.
Перепишем данную систему в виде
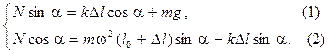
Разделив (1) на (2), получим:
tga = 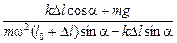 .
.
Решив данное уравнение относительно k, получаем ответ:
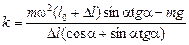 .
.
СТОП! Решите самостоятельно: С16, С18.
 Задача 15.5. Металлическое кольцо радиуса R = 10 см и с площадью поперечного сечения S = 1,0 см2 и массой т = 600 г раскручивают в горизонтальной плоскости (рис. 15.6). Известно, что если напряжение в металле превосходит величину s = 1,0×108 Па, металл разрушается. С какой угловой скоростью w надо вращать кольцо, чтобы оно разорвалось на части?
Задача 15.5. Металлическое кольцо радиуса R = 10 см и с площадью поперечного сечения S = 1,0 см2 и массой т = 600 г раскручивают в горизонтальной плоскости (рис. 15.6). Известно, что если напряжение в металле превосходит величину s = 1,0×108 Па, металл разрушается. С какой угловой скоростью w надо вращать кольцо, чтобы оно разорвалось на части?
| R = 10 см = 0,10 м S = 1,0 см2 = 1,0×10–4 м2 т = 600 г = 0,600 кг s = 1,0×108 Па |  Рис. 15.7 Рис. 15.7
|
| w = ? | |
Решение. Рассмотрим малый элемент кольца АВ массы Dт и длины Dl (рис. 15.7). Из рисунка видно, что  . Со стороны остальной части кольца на этот элемент действуют силы
. Со стороны остальной части кольца на этот элемент действуют силы 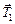 и
и 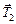 . Причем в силу симметрии |
. Причем в силу симметрии | 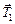 | = |
| = | 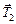 | = Т. Эти силы и сообщают элементу АВ центростремительное ускорение
| = Т. Эти силы и сообщают элементу АВ центростремительное ускорение  , направленное к центру кольца, причем а = w2R.
, направленное к центру кольца, причем а = w2R.
Проекции сил 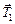 и
и 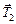 на ось
на ось 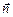 , как видно из DACD и DBEF, равны: AD = BE = Tn = Tsin
, как видно из DACD и DBEF, равны: AD = BE = Tn = Tsin 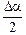 . Тогда в проекции на ось
. Тогда в проекции на ось 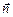 второй закон Ньютона примет вид
второй закон Ньютона примет вид
2Тп = Dтw2R. (1)
Если т – масса всего кольца, а l – его длина, то
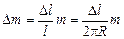 .
.
Подставляя в (1) значения Тп и Dт, получим
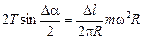 .
.
Учтем, что при Da ® 0 sin 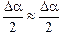 , а
, а 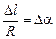 , тогда
, тогда
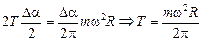 .
.
По определению напряжение равно
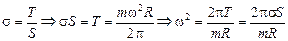 ,
,
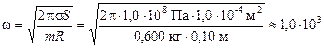 рад/с.
рад/с.
Как видим, угловая скорость требуется весьма приличная.
Ответ: кольцо разорвется при 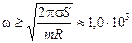 рад/с.
рад/с.
СТОП! Решите самостоятельно: D1, D2.
Дата добавления: 2016-04-11; просмотров: 2556;
