Тело на наклонной плоскости
Пусть небольшое тело находится на наклонной плоскости с углом наклона a (рис. 14.3,а). Выясним: 1) чему равна сила трения, если тело скользит по наклонной плоскости; 2) чему равна сила трения, если тело лежит неподвижно; 3) при каком минимальном значении угла наклона a тело начинает соскальзывать с наклонной плоскости.
а) 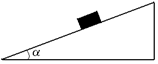 б)
б) 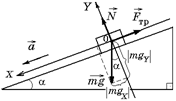
Рис. 14.3
Сила трения будет препятствовать движению, следовательно, она будет направлена вверх по наклонной плоскости (рис. 14.3,б). Кроме силы трения, на тело действуют еще сила тяжести 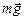 и сила нормальной реакции
и сила нормальной реакции  . Введем систему координат ХОУ, как показано на рисунке, и найдем проекции всех указанных сил на координатные оси:
. Введем систему координат ХОУ, как показано на рисунке, и найдем проекции всех указанных сил на координатные оси:
Х: FтрХ = –Fтр, NX = 0, mgX = mgsina;
Y: FтрY = 0, NY = N, mgY = –mgcosa.
Поскольку ускоряться тело может только по наклонной плоскости, то есть вдоль оси X, то очевидно, что проекция вектора ускорения  на ось Y всегда будет равна нулю: аY = 0, а значит, сумма проекций всех сил на ось Y также должна равняться нулю:
на ось Y всегда будет равна нулю: аY = 0, а значит, сумма проекций всех сил на ось Y также должна равняться нулю:
FтрY + NY + mgY = 0 Þ 0 + N – mgcosa = 0 Þ
N = mgcosa. (14.4)
Тогда сила трения скольжения согласно формуле (14.3) равна:
Fтр.ск = mN = mmgcosa. (14.5)
Если тело покоится, то сумма проекций всех сил, действующих на тело, на ось Х должна равняться нулю:
FтрХ + NХ + mgХ = 0 Þ –Fтр + 0 + mgsina = 0 Þ
Fтр.п = mgsina. (14.6)
Если мы будем постепенно увеличивать угол наклона, то величина mgsina будет постепенно увеличиваться, а значит, будет увеличиваться и сила трения покоя, которая всегда «автоматически подстраивается» под внешнее воздействие и компенсирует его.
Но, как мы знаем, «возможности» силы трения покоя не безграничны. При каком-то угле a0 весь «ресурс» силы трения покоя будет исчерпан: она достигнет своего максимального значения, равного силе трения скольжения. Тогда будет справедливо равенство:
Fтр.ск = mgsina0.
Подставив в это равенство значение Fтр.ск из формулы (14.5), получим: mmgcosa0 = mgsina0.
Разделив обе части последнего равенства на mgcosa0, получим:
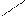
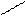


 Þ
Þ 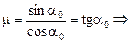 a0 = arctgm.
a0 = arctgm.
Итак, угол a, при котором начинается скольжение тела по наклонной плоскости, задается формулой:
a0 = arctgm. (14.7)
Заметим, что если a = a0, то тело может или лежать неподвижно (если к нему не прикасаться), или скользить с постоянной скоростью вниз по наклонной плоскости (если его чуть-чуть толкнуть). Если a < a0, то тело «стабильно» неподвижно, и легкий толчок не произведет на него никакого «впечатления». А если a > a0, то тело будет соскальзывать с наклонной плоскости с ускорением и безо всяких толчков.
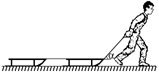
Задача 14.1. Человек везет двое связанных между собой саней (рис. 14.4,а), прикладывая силу F под углом a к горизонту. Массы саней одинаковы и равны т. Коэффициент трения полозьев по снегу m. Найти ускорение саней и силу натяжения Т веревки между санями, а также силу F1, с которой должен тянуть веревку человек для того, чтобы сани двигались равномерно.
| F a m m |
 а)
а)
|  б)
Рис. 14.4
б)
Рис. 14.4
|
| а = ? Т = ? F1 = ? |
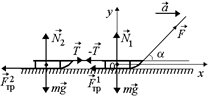
Решение. Запишем второй закон Ньютона для каждых саней в проекциях на оси х и у (рис. 14.4,б):
I у: N1 + Fsina – mg = 0, (1)
x: Fcosa – T – mN1 = ma; (2)
II у: N2 – mg = 0, (3)
x: T – mN2 = ma. (4)
Из (1) находим N1 = mg – Fsina, из (3) и (4) находим Т = mmg+ + ma. Подставляя эти значения N1 и Т в (2), получаем
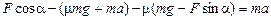 ,
,
отсюда
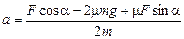 .
.
Подставляя а в (4), получаем
T = mN2 + ma = mmg + та =
= mmg + т 
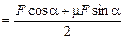 .
.
Чтобы найти F1, приравняем выражение для а к нулю:
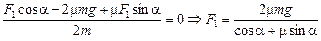 .
.
Ответ: 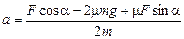 ;
;  ;
;
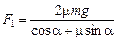 .
.
СТОП! Решите самостоятельно: В1, В6, С3.
Задача 14.2. Два тела массами т и М связаны нитью, как показано на рис. 14.5,а. С каким ускорением движется тело М, если коэффициент трения о поверхность стола m. Каково натяжение нити Т? Какова сила давления на ось блока?
| т М m | Решение. Запишем второй закон Ньютона в проекциях на оси х1 и х2 (рис. 14.5,б), учитывая, что 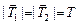 :
х1: Т – mMg = Ма, (1)
х2: mg – T = ma. (2)
Решая систему уравнений (1) и (2), находим: :
х1: Т – mMg = Ма, (1)
х2: mg – T = ma. (2)
Решая систему уравнений (1) и (2), находим:
|
| а = ? Т = ? R = ? |
а) 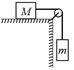 б)
б) 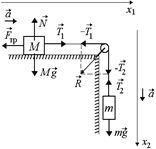 Рис. 14.5
Рис. 14.5
| 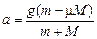 , ,
 .
Заметим, что а ³ 0, только если т – mМ ³ 0, т.е. т ³ mМ. Если т < mМ, то а = 0, при этом Т = mg.
На блок действует со стороны нити силы – .
Заметим, что а ³ 0, только если т – mМ ³ 0, т.е. т ³ mМ. Если т < mМ, то а = 0, при этом Т = mg.
На блок действует со стороны нити силы – 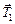 и и 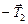 . Их равнодействующая . Их равнодействующая 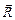 , как видно из рис. 14,5б, по модулю равна , как видно из рис. 14,5б, по модулю равна
 . .
|
Если грузы не движутся, то 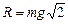 .
.
Ответ: 1) если т < mМ, то а = 0, Т = mg, 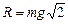 ; 2) если т ³ mМ, то
; 2) если т ³ mМ, то 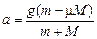 ,
,  ,
, 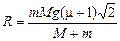 .
.
СТОП! Решите самостоятельно: В9–В11, С5.
Задача 15.3. Два тела массами т1 и т2 связаны нитью, перекинутой через блок (рис. 14.6). Тело т1 находится на наклонной плоскости с углом наклона a. Коэффициент трения о плоскость m. Тело массой т2 висит на нити. Найти ускорение тел, силу натяжения нити и силу давления блока на ось при условии, когда т2 < т1. Считать tga > m.
| т1, т2 a, m т2 < т1 tga > m | 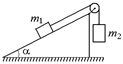 Рис. 14.6
Рис. 14.6
| Решение. Заметим, что из условия т2 < т1 нельзя заключить, в каком направлении движется система тел (и движется ли вообще). Поэтому сначала предположим, что тело т2 движется вверх (рис. 14.7). |
| а = ? Т = ? R = ? |
Рис. 14.7 
Запишем второй закон Ньютона в проекциях на оси х1 и х2, учитывая, что 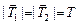 и
и 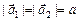 :
:
х1: т1gsina – Т – mm1g cosa = m1a,
х2: T – m2g = m2a.
Решая эту систему уравнений, находим:
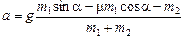 ,
,  .
.
Так как а >0, то
 . (1)
. (1)
Если неравенство (1) не выполняется, то груз т2 точно не движется вверх! Тогда возможны еще два варианта: 1) система неподвижна; 2) груз т2 движется вниз (а груз т1, соответственно, вверх).
Предположим, что груз т2 движется вниз (рис. 14.8).
Рис. 14.8 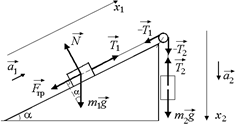
Тогда уравнения второго закона Ньютона на оси х1 и х2 будут иметь вид:
х1: Т – т1gsina – mm1gcosa = m1a,
х2: m2g – Т = m2a.
Решая эту систему уравнений, находим:
 ,
, 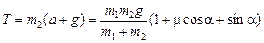 .
.
Так как а >0, то
 . (2)
. (2)
 Итак, если выполняется неравенство (1), то груз т2 едет вверх, а если выполняется неравенство (2), то – вниз. Следовательно, если не выполняется ни одно из этих условий, т.е.
Итак, если выполняется неравенство (1), то груз т2 едет вверх, а если выполняется неравенство (2), то – вниз. Следовательно, если не выполняется ни одно из этих условий, т.е.
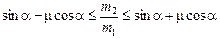 ,
,
система неподвижна.
Осталось найти силу давления на ось блока (рис. 14.9). Силу давления на ось блока R в данном случае можно найти как диагональ ромба АВСD. Так как
ÐADC = 180° – 2  ,
,
где b = 90°– a, то по теореме косинусов
R2 =  .
.
Отсюда  .
.
Ответ:
1) если 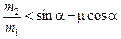 , то
, то 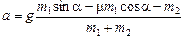 ,
, 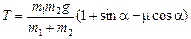 ;
;
2) если 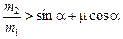 , то
, то 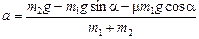 ,
, 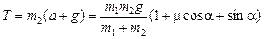 ;
;
3) если 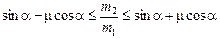 , то а = 0; Т = т2g.
, то а = 0; Т = т2g.
Во всех случаях  .
.
СТОП! Решите самостоятельно: В13, В15.
Задача 14.4. На тележку массой М действует горизонтальная сила F (рис. 14.10,а). Коэффициент трения между грузом т и тележкой равен m. Определить ускорение грузов. Какой должна быть минимальная сила F0, чтобы груз т начал скользить по тележке?
| M, т F m |
 а)
а)
|  б)
Рис. 14.10
б)
Рис. 14.10
|
| а1 = ? а2 = ? F0 = ? | ||
Решение. Сначала заметим, что сила, приводящая груз т в движение, – это сила трения покоя  , с которой тележка действует на груз. Максимально возможное значение этой силы равно mmg.
, с которой тележка действует на груз. Максимально возможное значение этой силы равно mmg.
По третьему закону Ньютона груз действует на тележку с такой же по величине силой –  (рис. 14.10,б). Проскальзывание начинается в тот момент, когда
(рис. 14.10,б). Проскальзывание начинается в тот момент, когда  уже достигла своего максимального значения
уже достигла своего максимального значения  , но система еще движется как одно тело массой т+М с ускорением
, но система еще движется как одно тело массой т+М с ускорением 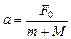 . Тогда по второму закону Ньютона
. Тогда по второму закону Ньютона
 .
.
Если сила F > F0, то каждое из тел движется со своим ускорением (а1 ¹ а2) и для каждого тела можно записать второй закон Ньютона:
т: mmg = та1, а1 = mg,
М: F – mmg = Mа2, 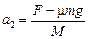 .
.
Ответ:  ; если F £ F0, то а1 = а2
; если F £ F0, то а1 = а2 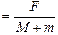 , если F > F0, то a1 = μg,
, если F > F0, то a1 = μg,  .
.
СТОП! Решите самостоятельно: С8, С9, С12.
Задача 14.5. Тело массы т находится на горизонтальном ленточном транспортере, движущемся со скоростью υ. Тело привязано нитью к вертикальной стене (рис. 14.11,а). Коэффициент трения между телом и лентой транспортера m. Какую силу следует приложить к телу в направлении, перпендикулярном движению транспортера, чтобы тело двигалось с постоянной скоростью и поперек транспортера? Считать и << υ.
| υ и m | а) 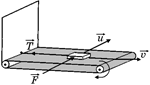
| 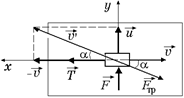 б) (вид сверху)
б) (вид сверху)
|
| F = ? | ||
Рис. 14.11
Решение. Выясним, куда направлена сила трения скольжения, действующая со стороны транспортера на тело массы т. Сила всегда направлена в сторону, противоположную движению тела в с.о., связанной с поверхностью, по которой скользит тело.
Найдем скорость тела относительно ленты транспортера 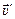 . Так как скорость груза относительно земли
. Так как скорость груза относительно земли 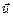 , а скорость транспортера
, а скорость транспортера 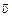 , то
, то 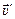 =
= 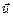 –
– 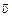 (рис. 14.11,б). Скорость
(рис. 14.11,б). Скорость 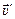 образует с осью х угол a:
образует с осью х угол a:
tga = и/υ. (1)
Сила трения  ¯
¯ 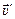 ,
,  . Считая, что тело будет двигаться с постоянной скоростью (
. Считая, что тело будет двигаться с постоянной скоростью ( 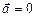 ), можем записать второй закон Ньютона в проекции на ось у:
), можем записать второй закон Ньютона в проекции на ось у:
у: 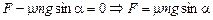 .
.
Учитывая, что и << υ, т.е. и/υ ® 0, можем считать tga » sina. Тогда согласно (1) имеем tga » sina = и/υ.
Отсюда получаем ответ: 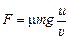 .
.
СТОП! Решите самостоятельно: С25, С26, D3.
Дата добавления: 2016-04-11; просмотров: 6774;
