Задачи очень трудные. D1. Замкнутая металлическая цепочка лежит на гладком горизонтальном диске, будучи свободно насажена на центрирующее ее кольцо

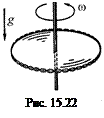
D1. Замкнутая металлическая цепочка лежит на гладком горизонтальном диске, будучи свободно насажена на центрирующее ее кольцо, соосное с диском (рис. 15.22). Диск приведен во вращение. Принимая форму цепочки за горизонтальную окружность, определить силу натяжения Т вдоль цепочки, если ее масса т = 150 г, длина l = 20 см и цепочка вращается с частотой w = 20 с^–1.

D2.Кольцевая цепочка массы m надета на горизонтальный диск радиуса R. Сила натяжения надетой цепочки Т. Найдите коэффи­циент трения между диском и цепочкой, если при вращении диска с угловой скоростью, равной или превышающей w, цепочка с него спадает.

D3.Тонкое резиновое кольцо радиуса R₀ и массы М₀ раскрутили вокруг оси до угловой скорости w. Найти новый радиус кольца, если коэффициент жесткости резины равен k.

D4.Обруч радиуса R = l м толчком «закручивают» вокруг столба диаметром d = 0,4 м. Какую скорость υ нуж­но придать обручу (υ – скорость его центра), чтобы он не съезжал вниз? Коэффициент трения m = =0,05.

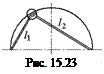D5.Шарик надет на про­волоку, согнутую в виде полу­окружности. На концах полуокружности закреплены упругие нити. Второй конец каждой нити связан с шариком (рис. 15.23). В начальный момент времени шарик скользил с постоянной по величине скоростью вдоль проволоки. Найти характер его последующего движения, если известно, что силы, с которыми нити действуют на шарик, пропорциональны их длине, F = kl. Весом шарика и си­лой трения его о проволо­ку можно пренебречь.

D6.Акробат, находясь на боковой поверхности ци­линдра, лежащего на очень шероховатом полу, перебирает ногами и движется с постоянной скоростью. Считая коэффициент трения ботинок акро­бата о поверхность цилиндра равным m, оп­ределить предельный угол a, который со­ставит с вертикалью радиус цилиндра, про­веденный в точку, в которой находится ак­робат. Чему будет равна сила трения ботинок акробата о цилиндр при этом? Масса акробата равна т.

D7.На обод массивного колеса массы М надет дополнительный груз малого размера и массы т, причем М/т = 15. С какой скоростью должно катиться колесо, чтобы оно подпрыгивало?

D8.Тонкостенный цилиндр катится по горизонтальной плоскости с ускорением а. Брусок А, размеры которого малы по срав­нению с радиусом цилиндра, скользит по внутренней поверхности цилиндра так, что угол между радиусом-вектором точки А и вертикалью остается постоянным. Найти этот угол, если коэффициент трения бруска о поверхность цилиндра равен k.