И центробежная силы

Читатель: Я все-таки до сих пор не понял, что такое центростремительная сила и что такое центробежная сила. Нельзя ли внести в этот вопрос полную ясность?

Автор: Ну что ж, давайте разберемся. Из самого термина «центростремительная сила» следует, что эта сила стремится к центру, т.е. направлена к центру. А центробежная сила – бежит от центра, т.е. направлена от центра окружности, по которой движется тело.

Рассмотрим шарик, который находится на вращающемся с постоянной скоростью диске, соединенный пружиной с осью вращения (рис. 16.1). Шарик движется с центростремительным ускорением, направленным к центру окружности. Это ускорение сообщает ему сила упругости пружины: , т.е. эта сила стремится к центру. Вот она-то и является, так сказать «по совместительству», еще и центростремительной силой.

Читатель: А какая же сила является центробежной?

Автор: Если пружина действует на шарик с силой 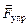, то по третьему закону Ньютона шарик действует на пружину с равной по величине и противоположной по направлению силой – 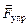. Эта сила направлена от центра. Она-то и является (тоже «по совместительству») центробежной силой.

Вообще же при равномерном движении тела по окружности центростремительной силой называется равнодействующая всех сил, действующих на тело.

Если тело движется по окружности под действием одной единственной силы, как, например, в случае спутника на круговой орбите, то эта реальная сила – сила тяготения является еще и центростремительной силой. Таким образом, термин «центростремительная сила» обозначает не какую-то дополнительную физическую силу, которая появляется при движении тела по окружности, а равнодействующую всех реальных физических сил.

Подчеркну, что центростремительная сила приложена к телу, движущемуся по окружности (спутнику, шарику, автомобилю и т.п.) со стороны других тел (Земли, пружины, дороги и т.п.). Что же касается центробежной силы, то здесь все настолько, я бы сказал, путано и несуразно, что будь на то моя воля, я бы этот термин вообще не вводил.

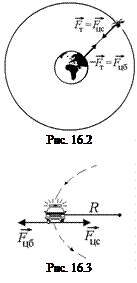Если говорить чисто формально, то центробежная сила – это векторная сумма сил, приложенных со стороны тела, движущегося по окружности к тем телам, которые вынудили его к этому движению. Например, в случае шарика, вращающегося на пружинке (см. рис. 16.1), центробежная сила – это сила, с которой шарик растягивает пружинку; в случае спутника, движущегося вокруг Земли по круговой орбите, центробежная сила – это сила, с которой спутник действует на Землю (рис. 16.2). В случае автомобиля, совершающего поворот, центробежная сила – это сила трения, с которой колеса действуют на дорогу (рис. 16.3).

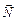Когда автомобиль совершает крутой поворот, пассажиров прижимает к стенке – сила реакции стенки сообщает им центростремительное ускорение (рис. 16.4). Сила 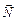– это центростремительная сила, а сила (– 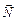), с которой пассажир действует на стенку, является центробежной силой.

Когда центростремительная сила обусловлена действием одного тела – шоссе, Земли, стенки автомобиля и т.д., центробежная сила есть просто сила противодействия этой центростремительной силе и имеет ту же природу.

Все бы ничего, но когда движение тела по окружности обусловлено действием двух и более тел, центробежная сила превращается в абстракцию, лишенную физического смысла.

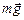Рассмотрим конический маятник (рис. 16.5). На шарик, вращающийся на нити, действуют две силы: сила реакции нити и сила тяжести . Центростремительной силой является равнодействующая этих сил: . _ _^

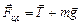Центробежной же силой в таком случае является векторная сумма сил (– ) и (– 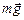), где (– ) – сила, с которой шарик действует на нить, а (– 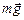) – сила, с которой шарик действует на Землю:

. (1)

Поскольку силы (– ) и (– 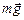) приложены к разным телам, говорить об их равнодействующей нельзя, а выражение (1) носит чисто умозрительный характер. То есть реальной силы, которая «бежит от центра», в данном случае просто нет!

Читатель: А что понимать под центростремительной силой в случае неравномерного движения по окружности?

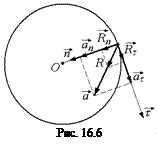
Автор: В этом случае ускорение тела имеет две составляющие: нормальное ускорение и тангенциальное (касательное) ускорение. Нормальное ускорение направлено к центру окружности, а тангенциальное – по касательной (рис. 16.6).

Поскольку по второму закону Ньютона равнодействующая сила равна 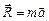, то вектор совпадает по направлению с вектором полного ускорения .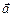

Вектор можно представить в виде суммы двух составляющих векторов: = 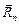+ (см. рис. 16.6). При этом и 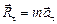. Величина и является в данном случае центростремительной силой. Ясно, что это может быть как реальная сила, так и чисто умозрительная величина.

Пример 16.1.Шарик скатывается по желобу и делает «мертвую петлю» (рис. 16.7). В точке А тело движется замедленно, причем равнодействующая сила . Центростремительная сила в данном случае – это сила нормальной реакции 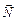, именно она сообщает шарику центростремительное ускорение.

Рис. 16.7

Пример 16.2.Шарик совершает колебания на нити в вертикальной плоскости. В произвольной точке А шарик движется с возрастающей по величине скоростью (рис. 16.8). На шарик действуют две силы: и 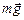. Если представить силу 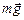в виде суммы двух составляющих векторов: 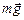= + 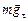, то центростремительная сила будет равна

;

.