Задачи очень трудные. D1.Система из трех одинаковых шаров, связанных одинаковыми пружинами, подвешена на нити (рис

D1.Система из трех одинаковых шаров, связанных одинаковыми пружинами, подвешена на нити (рис. 13.15). Нить пережигают. Найдите ускорения шаров сразу после пережигания нити.

D2.Концы легкой пружинки шарнирно прикреплены к стенке и бруску массой m = 0,25 кг, который удерживают на гори­зонтальной поверхности, растянув пружинку вдвое против ее дли­ны l₀ = 10 см в недеформированном состоянии (рис. 13.16). В этом положении ось пружины образует угол a = 30° с гори­зонтом. Найти ускорение а бруска сразу после того, как он будет отпущен. Жесткость пружины k = 80 Н/м.

СИЛА ТРЕНИЯ

Сила трения покоя

Путь некоторое тело находится на шероховатой горизонтальной поверхности. Приложим к нему горизонтальную силу , которую будем измерять с помощью динамометра, как показано на рис. 14.1.

Рис. 14.1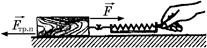

Будем постепенно увеличивать эту силу, что же мы увидим? Сила увеличивается, а тело как лежало неподвижно, так и лежит!

Согласно второму закону Ньютона такое поведение тела можно объ­яснить только одним: на него действует со стороны шероховатой по­верхности сила, равная по величине и противоположная по направле­ние силе . Эту силу, препятствующую движению тела, называют силой трения покоя:

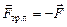. (14.1)

Таким образом, получается, что сила трения покоя не имеет опре­деленной величины: она как бы «автоматически подстраивается» под внешнее воздействие, чтобы удержать тело на месте.

Однако сила трения покоя не может возрастать до бесконечности: когда величина внешней силы превысит некоторое предельное значение F₀, тело начнет скользить по поверхности.

Величина F₀ представляет собой максимальное значение силы тре­ния покоя. Опытным путем установлено, что величина максимального значения силы трения покоя F₀ пропорциональна силе нормальной ре­акции N:

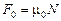. (14.2)

Безразмерный множитель m₀ называется коэффициентом трения покоя. Он зависит от материалов и шероховатости трущихся поверх­ностей.

Сила трения покоя всегда возникает при попытке сдвинуть одну трущуюся поверхность относительно другой (рис. 14.2).