Задачи средней трудности. В1.Два соприкасающихся бруска лежат на горизон­тальном столе, по которому они могут скользить без тре­ния

В1.Два соприкасающихся бруска лежат на горизон­тальном столе, по которому они могут скользить без тре­ния. Масса первого бруска m₁ = =2,00 кг, масса второго бруска т₂ = 3,00 кг. Один из брусков толкают с силой F₀ = 10,0 H (рис. 14.12). 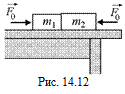Найти силу F, с которой бруски давят друг на друга в случае, если сила F, приложена: а) к бруску 1, б) к бруску 2.

В2. Решить задачу В1 в предположении, что коэф­фициент трения между бруском и столом равен k₁= 0,100 для бруска 1 и k₂= 0,200 для бруска 2.

В3. Решить задачу В2, положив k₁= 0,200 и k₂= 0,100. Сопоставить результаты задач В1, В2 и данной за­дачи.

В4. Два груза массами М₁ = 3 кг и М₂ = 5 кг лежат на гладком горизонтальном столе, связанные шнуром, который разрывается при силе натяжения Т = 24 Н. Какую максимальную силу F можно приложить к грузу М₁? к грузу М₂? Kaк изменится ответ, если учесть трение? Коэффициенты трения грузов о стол одинаковы.

В5. Три груза массой т = 1 кг каждый связаны нитью и дви­жутся по горизонтальной плоскости под действием силы F = 10 Н, направленной под углом a = 30° к горизонту. Опре­делить ускорение системы и силы натяжения нитей, если коэффициент трения μ = 0,1 (рис. 14.13).

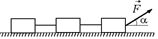
Рис. 14.13 Рис. 14.14

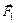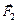В6. Два бруска массами т₁ и т₂, связанные нерастяжимой нитью, находятся на горизонтальной плоскости. К ним приложены силы и (рис. 14.14), составляющие с горизонтом углы a и b. Найти ускорение системы а и силу натяжения нити. Коэффициенты трения брусков о плоскость одинако­вы и равны k. Силы F₁ и F₂ не отрывают бруски от плоскости. Система движется влево.

В7. Два соприкасающихся бруска скользят по наклонной доске (рис. 14.15). Масса первого бруска т₁ = 2,00 кг, масса второго бруска т₂ = = 3,00 кг. Коэффициент трения между бруском и доской равен k₁= 0,100 для бруска 1 и k₂ = 0,200 для бруска 2. Угол наклона доски a = 45°.

1. Определить: а) ускоре­ние w, с которым движутся бруски, б) силу F, с которой бруски давят друг на друга.

2. Что происходило бы в случае k₁ > k₂.

В8.Доска А движется по горизонтальному столу под действием силы натяжения привязанной к ней нити. Нить пере­кинута через прикрепленный к столу блок и прикреплена к другой доске В, падающей вниз.

1. Определить силу натяжения нити Т, если масса доски А m₁ = 200 г, масса доски В т₂ = 300 г, коэффициент трения k = 0,25. Масса блока ничтожно мала.

2. Как изменится ответ, если доски поменять местами?

3. Определить силу F, действующую на ось блока в случаях (1) и (2).

В9. На брусок массы т₁ = 0,18 кг по­ставлена гиря массы т₂ = 2 кг (рис. 14.16). С помощью нити, перекинутой через блок, брусок с гирей скользит с постоянной скоростью по доске, когда на чашку массы т₃ = =0,18 кг положена гиря массы т₄ = 0,5 кг. Найти коэффициент трения k между бруском и доской.

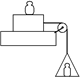
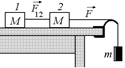
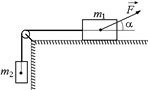
Рис. 14.16 Рис. 14.17 Рис. 14.18

В10.На горизонтальном столе лежат два тела массы М = 1,000 кг каждое. Тела связаны невесомой нерастяжимой нитью (рис. 14.17). Такая же нить связывает тело с грузом массы т = 0,500 кг. Нить может скользить без трения по изогнутому желобу, укрепленному на краю стола. Коэффициент трения первого тела со столом k₁ = 0,100; второго тела k₂= 0,150. Найти: а) ускорение ω, с которым движутся тела; б) натяжение F₁₂ нити, связывающей тела 1 и 2; в) натяжение F нити, на которой висит груз.

В11.Определить ускорение тел в системе, показан­ной на рис. 14.18. Коэффициент трения между телом и столом μ = 0,1. Трением в блоке, массами блока и нити пренебречь. Нить считать нерастяжи­мой, т₁ = 1,5 кг, т₂ = 0,5 кг, F = 10,0 H, a = 30°.

В12.В установке (рис. 14.19) известны угол a и коэффициент трения k между телом т₁ и наклонной плоскостью. Массы блока и нити пренебрежимо малы, трения в блоке нет. Вначале оба тела неподвижны. Найти отношение масс m₂/т₁, при котором тело m₂ начнет: а) опускаться; б) подниматься.

Рис. 14.19 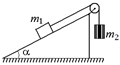Рис. 14.20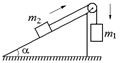

В13.Наклонная плоскость (см. рис. 14.19) составляет угол a = 30° с горизонтом. Отношение масс тел m₂/m_l = h = 2/3. Коэффициент трения между телом т₁ и плоскостью k = 0,10. Массы блока и нити пренебрежимо малы. Найти модуль и направление ускорения тела т₂, если система пришла в движение из состояния покоя.

В14. По наклонной плоскости (угол наклона a) движется тело массой т₂, связанное нерастяжимой нитью, перекинутой через блок, с телом массы m₁ (m₁ > m₂) (рис. 14.20). Коэффициент трения между грузом m₂ и наклон­ной плоскостью равен k. Найти силу, действующую на ось блока со стороны плоскости. (Массами блока и нити пренебречь, трение в оси отсутствует.)

В15.Два груза с одинаковыми массами связаны между собой нитью, перекинутой через невесомый блок. Плоскости, на которых находятся грузы, составляют с гори­зонтом углы a и b (рис 14.21). Найти ускорение а грузов и силу натяжения F нити. Коэффициент трения скольжения грузов о плоскость одинаков и равен k. При каком коэффициенте трения k₁, грузы будут находиться в покое?

Рис. 14.21 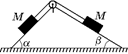Рис. 14.22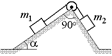

В16.Найти абсолютные значения ускорений а₁ и а₂, с которыми может двигаться система из двух брусков, связанных тонкой нитью, переброшенной через легкий блок. Он укреплен на оси в вершине прямого угла призмы (рис. 14.22). Призма неподвижна. Угол a = 30°. Массы брусков т₁ = 0,10 кг, т₂ = 0,60 кг. Коэффициент трения брусков о грани призмы m = 0,20. Ветви нити па­раллельны граням призмы. Трением в оси блока пренебречь.

В17.Гибкую веревку или шнур растяните на столе перпендикулярно краю стола. Постепенно свешивайте часть веревки со стола до тех пор, пока веревка не придет в движение. Измерив длину всей веревки l и длину свешенной части х, определите коэффициент трения m.

Задачи трудные

С1. Три одинаковых груза массой т = 2 кг каждый соединены двумя одинаковыми пружинами жесткостью k = 25 Н/м (рис. 14.23). К правому грузу приложена сила F = 30 Н, при этом все грузы движутся с одинаковыми ускорениями. Определить ускорение системы грузов, а также определить, на сколько длина пружины между первым и вторым грузом отличается от длины пружины между вторым и третьим грузом. Коэффициент трения между каждым из грузов и плоскостью равен m = 0,1.

Рис. 14.23 Рис. 14.24

С2.п + 1 одинаковых грузов массой m каждый соединены друг с другом п одинаковыми невесомыми пружинами (рис. 14.24). К крайнему грузу приложена некоторая сила , под действием которой система движется с ускорением а в горизонтальном направлении. Определить величину силы F и изменение длины каждой пружины, если коэффициент трения между грузом и плоскостью равен f и жесткость пружины равна k.

С3.По наклонной плоскости скользят два тела одинаковой массы, связанные нитью. Сила натяжения нити Т. Трения между одним телом и доской нет. Определите силу трения между доской и другим телом.

С4. Два бруска с одинаковыми массами т скреплены нитью и находятся на наклонной плоскости с углом наклона a. Определить силу натяжения нити Т при движении брусков вдоль наклонной плоскости, если коэффициент трения k верх­него бруска о плоскость в два раза больше коэффициента трения нижнего.

С5. На краю стола установлен блок с неподвижной осью, через который перекинута нить, связывающая три груза. Два из них лежат на поверхности стола и в свою очередь связаны между собой нитью (рис. 14.25), третий висит, не касаясь стола. Массы грузов, лежащих на столе, равны М/2 каждая, масса третьего груза М. Коэффициент трения между столом и грузами k. На висящий груз помещают перегру­зок массы т и 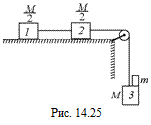система приходит в движение. Найти ускорение грузов, силу натяжения нити, свя­зывающей грузы 1 и 2, силу, с которой перегрузок давит на груз 3. При каком коэффициенте трения система вообще не придет в движение? Рассмотреть случай, когда k = 0, и найти величину ускорения, с которым в этом случае двигалась бы система.

С6. Какова сила трения, действующая на брусок массой m (рис. 14.26), с каким ускорением движутся грузы и какова сила натяжения нити, если h = 60 см, l = 1 м, т = 0,5 кг, m = 0,25? Решить задачу при следующих значе­ниях массы М: а) 0,1 кг; б) 0,25 кг; в) 0,3 кг; г) 0,35 кг; д) 0,5 кг.

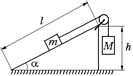
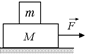
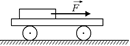
Рис. 14.26 Рис. 14.27 Рис. 14.28

С7.Тело массой т = 50 кг находится на другом теле массой М = 150 кг (рис. 14.27). Максимальное значе­ние силы трения покоя между этими телами харак­теризуется коэффициентом m = 0,3. Найти минималь­ную силу, при действии которой на нижнее тело происходит сдвиг верхнего тела относительно него. Трением нижнего тела о поверхность, на которой оно находится, пренебречь.

С8.Тележка весом в 20 кгс может ка­титься без трения по горизонтальному пути. На тележке лежит брусок весом в 2 кгс (рис. 14.28). Коэффициент трения между бруском и тележкой k = 0,25. К бруску приложена сила один раз F₁ = 200 гс, в другой раз F₂ = 2 кгс. Определить, какова будет сила трения между бруском и тележкой и с какими ускорениями будут двигаться брусок и тележка в обоих случаях.

С9.Брусок массой М₁ находится на доске массой М₂ расположенной на горизон­тальной плоскости. Коэффициент трения скольжения между бруском и доской равен k₁, а между доской и плоскостью k₂. Найти минимальную горизонтальную силу F, при действии которой на доску происходит сдвиг бруска относительно доски.

С10.На доске массы 1 кг, расположенной на горизонтальном столе, лежит брусок массы 2 кг. Коэффициент трения между доской и поверхностью стола равен 0,5; между бруском и доской – 0,25. Каково будет ускорение бруска относительно доски и стола, если к доске приложить силу 19,6 Н? 29,4 Н?

С11.Бруски A и В массами т₂ и m₁ находятся на столе (рис 14.29). К бруску В приложена сила , направленная под углом a к горизонту. Найти ускорения движения брусков, если коэффициенты трения брусков друг о друга и бруска о стол равны соответственно k₁ и k₂. Сила трения между поверхностями максимальна.

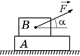
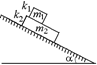
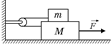
Рис. 14.29 Рис. 14.30 Рис. 14.31

С12. На наклонную плоскость с углом наклона a помещена плоская плита массы т₂, а на нее – брусок массы т₁. Коэффициент трения между бруском и плитой k₁. Определить, при каких значениях коэффициента трения k₂ между плитой и плоскостью плита будет двигаться, если известно, что брусок скользит по плите (рис. 14.30).

С13. На гладком горизонтальном столе лежит брусок массы М = 2 кг, на котором находится брусок массы т = 1 кг. Оба бруска соединены легкой нитью, перекинутой через блок (рис. 14.31). Какую силу надо приложить к нижнему бруску, чтобы он начал двигаться от блока с постоянным ускорением a = g/2? Коэффициент трения между брусками k = 0,5. Трением между нижним бруском и столом пренебречь.

С14. На доске массы т₂ лежит тело массы т₁, к которому привязана нить, перекинутая через блок (масса блока равна нулю). Ко второму концу нити привязан груз М (рис 14.32). Коэффициент трения между доской и телом k₁, коэффициент трения между доской и столом k₂. При какой максимальной массе груза тело не соскользнет с доски?

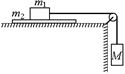Рис. 14.32 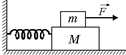Рис. 14.33

С15. По бруску массой М, лежащему на гладкой горизонтальной поверхности и удерживаемому пружиной (рис. 14.33), скользит равномерно брусок массой т под действием силы . Покажите зависимость ускорения бруска М и силы трения между соприкасающимися поверхностями от времени.

С16. На гладкой горизонтальной плоскости лежит доска и на ней брусок массы т = 1,0 кг, соединенный с точкой О резиновым шнуром. Коэффициент трения между бруском и доской k = 0,2. Доску начали медленно перемещать по плоскости до положения, при котором брусок начал скользить по ней. Это произошло в момент, когда шнур отклонился на угол a = 30°. Найти силу натяжения шнура в этот момент (рис. 14.34).

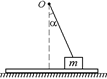
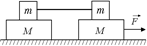
Рис. 14.34 Рис. 14.35 Рис. 14.36

С17.Три тела одинаковой массы т = 1 кг находятся друг на друге (рис. 14.35). Коэффициент трения между телами 1 и 2 равен k₁ = 0,1, a между телами 2 и 3 – k₂ = 0,2. Коэффициент трения между полом и телом 3 равен k₃ = 0,1. Тело 2 тянут с некоторой горизонтальной силой . При какой силе возможно такое движение этих трех тел, при котором тела 1 и 3 остаются в покое друг относительно друга? Определить ускорения а₁, а₂ и а₃ всех трех тел при этом движении.

С18. На гладком горизонтальном столе расположена система грузов (рис. 14.36). Коэффициент трения между грузами М и т равен m. Грузы массы т соединены невесомой нерастяжимой нитью. Первый нижний груз тянут вдоль стола с силой , как указано на рисунке. Найти ускорения всех грузов системы.

С19.Брусок весом 40 H зажат между двумя досками силами по 50 Н. Коэффициент трения между поверхностью бруска и доской равен 0,50. Какую силу следует приложить к бруску, чтобы он двигался равномерно вниз? равномерно вверх? вниз с ускоре­нием 0,2 м/с²? вверх с тем же по модулю ускорением?

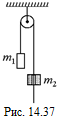
С20.Через легкий вращающийся без трения блок перекинут шнурок. На одном конце шнурка привязан груз массы m₁. По другому концу шнурка может скользить кольцо массы т₂ (рис. 14.37).

1. С каким ускорением а движется кольцо, если груз m₁ неподвижен? Чему равна сила трения F_тр кольца о шнурок?

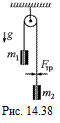2. Кольцо соскальзывает с постоянным относительно шнур­ка ускорением а₂. Найти ускорение а₁ груза массы m₁ и силу трения F_тр кольца о шнурок. Массой шнурка можно пренебречь; считать, что груз т₁ опускается.

С21.Нить, перекинутая через блок с неподвижной осью, пропущена через щель. На концах нити подвешены грузы, массы которых m₁ и т₂ (рис. 14.38). Определите ускорения грузов, если при движении нити на нее со стороны щели действует постоянная сила трения F_тp.

С22.На наклонной плоскости, составляющей угол a с горизонтом, ле­жит доска. С каким ускорением и в каком направлении должен бежать по доске человек, чтобы доска оставалась неподвижной на плоскости? Массы человека и доски т и М соответственно, трением доски о плоскость пренебречь (рис. 14.39).

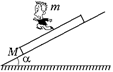
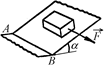
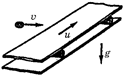
Рис. 14.39 Рис. 14.40 Рис. 14.41

С23.По легкому клину с углом a, лежащему на гори­зонтальном полу, скользит тело. Коэффициент трения между клином и полом k. Каков должен быть минимальный коэффициент трения k₁ между телом и клином, чтобы последний оставался неподвижным? Массу клина при расчетах не учитывать.

С24. Брусок массы т = 0,25 кг лежит на шероховатой плоской поверхности, наклоненной к горизонту под углом a = 17° (рис. 14.40). С какой минимальной горизонтальной си­лой F₀, параллельной ребру АВ дву­гранного угла, следует натянуть тонкую нить, привязанную к бруску, чтобы он стал скользить по шерохо­ватой поверхности? Коэффициент тре­ния скольжения бруска о поверхность k = 0,61.

С25.Лента горизонтального транспортера движется со скоростью и. На ленту по касательной к ней влетает шайба, начальная скорость υ кото­рой перпендикулярна краю ленты (рис. 14.41). Найдите максимальную ширину ленты, при которой шайба достигнет другого ее края, если коэффициент трения между шайбой и лентой m.

С26.По горизонтальной поверхности движется брусок с постоянной скоростью υ₀. Коэффициент трения бруска о поверхность равен k. Найти минимальную силу, с которой надо подействовать на брусок, чтобы он сместился в направлении, перпендикулярном к движению.