Возможные случаи приведения системы сил, произвольно расположенных в плоскости

При приведении произвольной плоской системы сил к заданному центру возможны следующие случаи.

Случай 1. 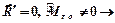система сил приводится к паре сил, момент которой равен главному моменту системы сил относительно центра приведения. В этом случае главный момент не зависит от центра приведения, потому что момент пари 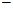свободный вектор. Для плоской системы сил это алгебраический момент, который можно приложить в любой точке тела.

Случай 2. 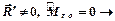система сводится к одной силе, равнодействующей 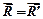, приложенной в центре приведения.

Случай 3. .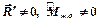

Покажем, что в этом случае система сил также приводится к равнодействующей, которая приложена не в центре приведения, а в другой точке.

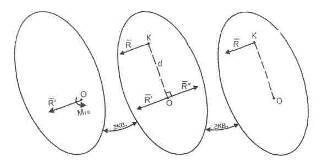
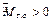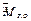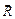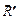Пусть (рис. 5.2 а). Изобразим пару сил с моментом двумя силами и , приложенными в точке К и в точке О, соответственно, выбрав лечо 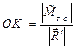(рис. 5.2 б). Тогда 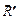компенсирует силу и останется одна сила 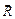, приложенная в точке К, то есть равнодействующая (рис. 5.2 в).

а б в

 

Рисунок 5.2

Вывод.

Случай 4. Уравновешенная система сил

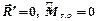. (5.4)

Это геометрическая форма уравнений равновесия произвольной плоской

системы сил.