Теорема о параллельном переносе силы
Из предыдущего (п. 1.2) известно, что вектор силы – это скользящий вектор в пределах одного твердого тела. Как считаете: изменится ли действие силы на тело, если силу перенести параллельно в другое место тела? Например, стол потянем за правый угол, за середину, или за левый угол. Чтобы ответить на этот вопрос рассмотрим следующую теорему.
Доказательство теоремы [1, 2].
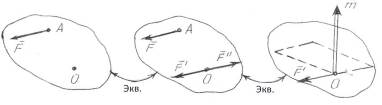
Рассмотрим силу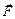 
, которая приложена в точке А твердого тела (рис. 4.1). Возьмем произвольную точку О и приложим в этой точке О две силы 
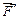и 
, которые взаимно уравновешиваются; модули всех трех сил одинаковые. Поэтому системы сил эквивалентны
,
где 
– момент присоединенной пары, который равен моменту силы 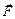относительно точки О. Вектор–момент перпендикулярен плоскости действия пары сил 
.. (4.1)
|
Рисунок 4.1
Теорема.
| При параллельном переносе силы в произвольную точку О получаем силу, которая равна заданной силе, и пару сил, момент которой геометрически равен моменту заданной силы относительно точки переноса. |
В дальнейшем точку О, куда переносится сила, называют точкой приведения, а пару сил, которая при этом возникает, называют присоединенной парой.
Конечно, если точка О лежит на линии действия силы, то момент присоединенной пары равен нулю, то есть получим только силу. Еще раз убеждаемся, что сила – скользящий вектор.
Теорема Пуансо
Заданная система сил 
, которые приложены в точках А1, А2,…, Аn к свободному пространственному твердому телу и как угодно направлены в пространстве (рис. 4.2 а).
|
а б в
Рисунок 4.2
Выберем произвольную точку О за центр приведения и перенесем все силы в точку О. Согласно с теоремой о параллельном переносе каждой силы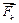 
(п. 4.1) из точки Ак в точку О (к = 1, 2,…, n), имеем
Следовательно, на первом этапе (рис.4.2 б) получили систему сходящихся сил, которая пересекается в точке О и систему пар сил, моменты которых равны моментам соответствующих сил относительно точки О. Моменты присоединенных пар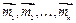 
на рис.4.2 б перпендикулярны плоскостям соответствующих заштрихованных треугольников.
.
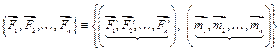| Система пространственных сходящихся сил | Система пар в пространстве |
Второй этап: заменим систему сходящихся сил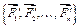 
одной силой – равнодействующей (формула (2.3))
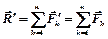. (4.2)
Заменим систему пар сил (рис. 4.2 в), расположенных в пространстве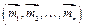 
одной парой (формула (3.6))
.
Момент результирующей пары в данном случае называют главным моментом.
Главный момент системы сил 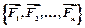 относительно точки О равен геометрической сумме векторных моментов сил системы
относительно этой точки.
|
. (4,3)
Для системы сил, расположенных в одной плоскости, главный момент будет алгебраической величиной, а не векторной.
Замечание.
Силу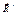 
нельзя считать равнодействующей заданной системы сил 
, (она является равнодействующей для системы сил 
) потому что она одна неэквивалентная заданной системе сил, так как есть еще пара сил. Поэтому 
– главный вектор системы сил , а не равнодействующая!
Следовательно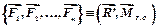 
. (4.4)
Теорема Пуансо.
| Систему сил, расположенных произвольно в пространстве, всегда можно привести к одной силе, которая равна ее главному вектору (и приложена в центре приведения) и к паре сил, момент которой геометрически равен главному моменту системы силы относительно центра приведения. |
Вспомним, что главный вектор можно получить двумя способами – геометрическим (формула (1.1)) и аналитическим (формулы (1.2)–(1.4)).
Предлагается ответить на вопрос: Какая из величины – главный вектор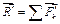 
, или главный момент относительно точки О 
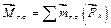не изменится, если выбрать другую точку за центр приведения?
Ответ…? Ответ следует из самого определения момента силы относительно точки, конечно, зависит от этой точки. То есть, главный момент – вектор, связан с центром приведения. Главный вектор, при этом, не зависит от центра приведения.
Пользуясь методом приведения системы сил к заданному центру, ниже рассмотрим вопросы, связанные с решением двух задач статики. Для системы сил, произвольно расположенной в плоскости в теме 5 (5.1–5.4), а затем, в теме 6
(6.1–6.6) в той же последовательности рассмотрим решение двух задач статики для системы силы произвольно расположенных в пространстве.
Вопросы для самоконтроля по теме 4
1. Что называют главным вектором системы силы? Как его определить?
2. Что называют главным моментом плоской системы сил, относительно точки О?
Как его определить?
3. Что называют главным моментом пространственной системы сил, относительно точки О? Как его определить?
4. Можно ли силу перенести параллельно себе в другую точку твердого тела?
Как это сделать?
5. Сформулируйте основную теорему статики (теорему Пуансо).
6. Изменится ли главный вектор, если поменять центр приведения? А главный момент?
Дата добавления: 2016-03-15; просмотров: 1967;