Эквивалентность пар сил

Теорема об эквивалентности пар.

Докажем первые два утверждения.

Пусть на свободное тело действует пара сил 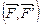момент которой равняется 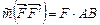(рис. 3.8). Приложим противоположно направленные равные по модулю силы 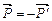. Сложим попарно силы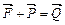 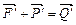. Тогда получим 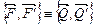, то есть вместо пары сил 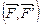имеем пару сил .

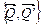Момент новой пары сил 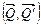равен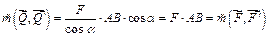

Как известно, сила – скользящий вектор, то есть можно считать, что силы 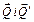приложены в других точках, например А₁ и В₁. Таким образом, новая пара сил 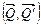имеет другое плечо, повернута по отношению к паре 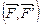и находится в другом месте плоскости действия пар сил π.

Рисунок 3.8

В Дополнении А.4 доказано третье утверждение о том, что, не изменяя состояния тела, пару сил можно перенести в другую плоскость, параллельную плоскости действия пары сил.

Следовательно, можно сделать вывод. Элементы пары сил: сила, плечо, плоскость действия не являются существенными в пределах одного твердого тела.

Это подтверждают и рассуждения проиллюстрированные рисунком 3.5 о том, что вектор-момент пары сил равен геометрической сумме вектор-моментов сил пары относительно произвольной точки, так как вращательное действие пары сил 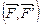не зависит от точки, вокруг которой мы измеряли суммарное вращательное действие каждой силы пары. (Можно убедиться в этом если вместо точки О, взять точку О_1.

На плоскости моменты пар сил изображаем дуговыми стрелками, которые несут информацию о направлении вращения парой сил: по ходу часовой стрелке, или против (рис. 3.7; 3.13).

Вопрос. Одинаковое ли действие пары сил на конструкцию (рис. 3.9, 3.10), если пару сил перенести в другое место:

1) конструкция сварена в точке С (рис. 3.9)

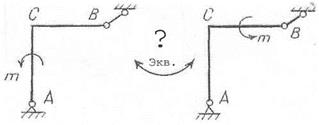Рисунок 3.9

2) конструкция составлена из двух частей в шарнире С (рис. 3.10)

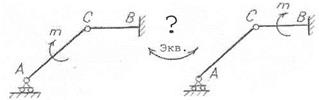
Рисунок 3.10