Момент силы относительно точки

| Мерой вращательного действия силы вокруг точки, лежащей в одной плоскости с силой, является алгебраический момент силы относительно точки. |
| Алгебраический момент силы относительно точки равен произведению модуля силы на плечо, взятому со знаком « + », если сила вращает тело вокруг этой точки против хода часовой стрелки и со знаком « – », если по ходу часовой стрелки. |
Обозначаем алгебраический момент 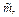 чтобы отличать его от модуля
чтобы отличать его от модуля 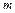
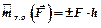 , (3.1)
, (3.1)
где h – плечо силы 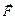 относительно т. О – это длина перпендикуляра, опущенного из точки О на линию действия силы
относительно т. О – это длина перпендикуляра, опущенного из точки О на линию действия силы 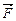 .
.
На рис. 3.1 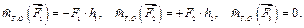
На практике силы могут быть расположены в разных плоскостях, тогда вращательное действие силы измеряет момент силы относительно точки, как вектор – векторный момент.
Рассмотрим силы действующие на пространственное тело М, закрепленное в точке О. Силы расположены в разных плоскостях: 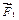 принадлежит плоскости Оzy,
принадлежит плоскости Оzy, 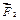 принадлежит плоскости Охy. Соединим точки А1 и А2 с точкой О. Выясним: вокруг каких осей могут вращать эти силы?
принадлежит плоскости Охy. Соединим точки А1 и А2 с точкой О. Выясним: вокруг каких осей могут вращать эти силы? 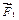 вращает вокруг оси Ох, покажем
вращает вокруг оси Ох, покажем 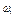 – скорость вращения вокруг оси Оx. Сила
– скорость вращения вокруг оси Оx. Сила 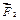 вращает вокруг оси ОZ покажем
вращает вокруг оси ОZ покажем 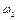 – скорость вращения вокруг оси ОZ. Отсюда делаем выводы о том, куда направлены моменты
– скорость вращения вокруг оси ОZ. Отсюда делаем выводы о том, куда направлены моменты 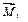 и
и 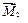 .
.
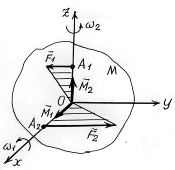 Рисунок 3.2
Рисунок 3.2
|
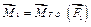 направлен по оси Ох; направлен по оси Ох;
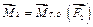 направлен по оси Оz. направлен по оси Оz.
|
| Векторный момент (вектор-момент) силы относительно точки – это вектор, перпендикулярный к плоскости, которая проходит через силу и точку. Направлен момент туда, откуда видно, что сила пытается повернуть тело против хода часовой стрелки (рис. 3.2). |
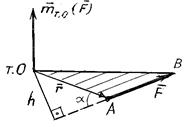 Рисунок 3.3
Рисунок 3.3
|
Если вспомнить, чему равно векторное произведение векторов 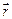 и и 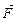 , в котором , в котором
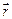 – радиус-вектор точки приложения силы (точки А, рис. 3.3), а – радиус-вектор точки приложения силы (точки А, рис. 3.3), а 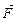 – вектор силы, то мы получим – вектор силы, то мы получим
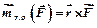 . (3.2) . (3.2)
|
Формула (3.2) учитывает все факторы, от которых зависит вращательное действие силы вокруг точки О:
– величина векторного произведения равняется 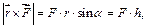
это и есть модуль векторного момента силы 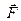 относительно точки О;
относительно точки О;
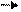
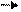
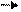
 – направление векторного момента также совпадает с направлением векторного произведения
– направление векторного момента также совпадает с направлением векторного произведения 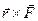 , который перпендикулярен к плоскости, в которой расположены вектора
, который перпендикулярен к плоскости, в которой расположены вектора 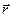 и
и 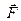 и направлен туда, откуда можно наложить вектор
и направлен туда, откуда можно наложить вектор 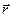 на вектор
на вектор 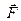 по меньшему углу против хода часовой стрелки.
по меньшему углу против хода часовой стрелки. 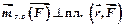 . Следовательно, вектор – момент силы относительно центра (точки) геометрически равен векторному произведению радиуса-вектора точки приложения силы относительно центра на вектор силы.
. Следовательно, вектор – момент силы относительно центра (точки) геометрически равен векторному произведению радиуса-вектора точки приложения силы относительно центра на вектор силы.
Дата добавления: 2016-03-15; просмотров: 1294;
