Теорема о равновесии трех непараллельных сил
Пусть известно, что тело под действием трех сил, расположенных в одной плоскости, находится в равновесии, т. е. 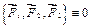 . Сила
. Сила 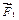 приложена в точке
приложена в точке 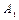 , сила
, сила 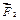 приложена в точке
приложена в точке 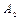 .
.
Вопрос: какой должна быть сила 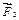 , которая бы уравновесила силы
, которая бы уравновесила силы 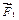 и
и 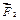 ?
?
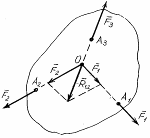 Рисунок 2.3
Рисунок 2.3
|
Ответ: найдем равнодействующую сил 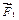 и и 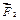 , продолжив их до пересечения в точке О и построив диагональ параллелограмма на силах , продолжив их до пересечения в точке О и построив диагональ параллелограмма на силах 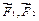 . . 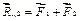 . Сила . Сила 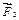 будет равняться силе будет равняться силе 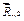 по величине, но противоположна ей по направлению и обязательно проходит через точку О. То есть, линии действия сил по величине, но противоположна ей по направлению и обязательно проходит через точку О. То есть, линии действия сил 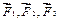 пересекаются в одной точке. Теорема доказана. пересекаются в одной точке. Теорема доказана.
| ||
| Три непараллельные силы, которые действуют на твердое тело в одной плоскости, уравновешиваются только в том случае, если их линии действия пересекаются в одной точке. | |||
Внимание!
Эта теорема является только необходимым, но не достаточным условием уравновешивания трех сил. То есть обратное несправедливо: если три силы пересекаются в одной точке, то это еще не значит, что они уравновешены. Надо проверить выполнение геометрического или аналитического условий равновесия сходящихся сил. Эту теорему часто используют для определения линии действия реакции связи, если эта линия, согласно классификации связей, неизвестна и на свободный объект действуют только три силы.
Пример (для самостоятельной работы)
Определить линию действия реакции шарнира А.
Дано: 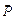 – сила тяжести тела (рис. 2.4 а, б, в).
– сила тяжести тела (рис. 2.4 а, б, в).
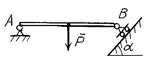
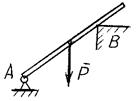
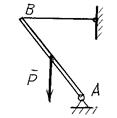
а б в
Рисунок 2.4
Дата добавления: 2016-03-15; просмотров: 1573;
