Главный вектор системы сил равняется геометрической сумме этих сил.
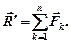 (1.1)
(1.1)
Обозначаем главный вектор 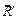 , а n – количество сил системы. Для нахождения главного вектора
, а n – количество сил системы. Для нахождения главного вектора 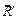 существует два способа.
существует два способа.
Геометрический способ
Если есть возможность точно отложить в масштабе каждую силу системы, начиная с точки О, то их откладывают одна за другой, то есть строят силовой многоугольник.
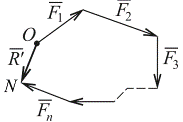 Рисунок 1.7
Главный вектор соединяет начало первой силы (точка О) с концом последней (точка N).
Рисунок 1.7
Главный вектор соединяет начало первой силы (точка О) с концом последней (точка N).
| Аналитический способ
Применяется, когда известны координаты векторов сил 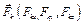 ,
k = 1, 2, …, n. Тогда проекции главного вектора на оси координат равняются: ,
k = 1, 2, …, n. Тогда проекции главного вектора на оси координат равняются:
 (1.2)
Модуль главного вектора равняется: (1.2)
Модуль главного вектора равняется:
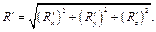 (1.3)
Направление главного вектора в пространстве определяется за направляющими косинусами: (1.3)
Направление главного вектора в пространстве определяется за направляющими косинусами:
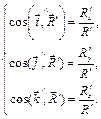 (1.4) (1.4)
|
Если силы расположены в одной плоскости Oxy, то многоугольник (рис. 1.7) будет плоским, а в формулах(1.2)–(1.4) отсутствует составляющая 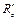 .
.
6. Равнодействующая системы сил – это одна сила, которая действует так же как система сил, то есть она эквивалентна системе сил. Обозначаем вектором 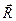 равнодействующую системы сил.
равнодействующую системы сил. 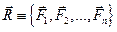 .
.
1.3 Основные понятия раздела «Статика». Вторая группа понятий, связанная с материальным объектом
Вторая группа понятий, связанная с материальным объектом изучения. К ним относятся:
1) абсолютно твердое тело;
2) свободное тело;
3) несвободное тело;
4) связь;
5) реакция связи.
1.3.1 Абсолютно твердым телом (в дальнейшем АТТ) называют тело, форма и размеры которого не изменяются под действием сил. Конечно, таких тел в технике не существует, но эта абстракция вводится для упрощения многих теоретических изложений и является оправданной для решения многих практических задач.
1.3.2 Свободное тело – тело, на движение которого не наложено никаких ограничений.
Вопрос. Сколько степеней свободы имеет свободное тело в пространстве? (Ответ: шесть).
1.3.3 Несвободное тело – тело, для которого хотя бы какие-то перемещения в пространстве невозможны.
Вопрос. В технике какие тела? (Ответ: несвободные).
1.3.4 Связи – тела, которые ограничивают движение несвободного тела в пространстве.
Рассмотрим примеры:
а) мост крепится в точках А и В (рис. 1.8) – связи в точках А и В;
б) балкон замурован в стенку (рис. 1.9) – связь наложена на часть балки возле точки А.
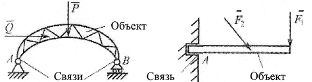
Рисунок 1.8 Рисунок 1.9
Выясним, как действует, например, гладкий (без трения) стол на предмет М, что на нем лежит (рис. 1.10 а). На предмет действуют силы 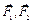 . Предмет не двигается, потому что со стороны стола действует сила
. Предмет не двигается, потому что со стороны стола действует сила 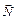 перпендикулярная к плоскости стола
перпендикулярная к плоскости стола
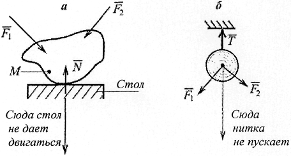
Рисунок 1.10
Шарик висит на нити, на него действуют силы 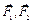 (рис. 1.10 б) , шарик не двигается, потому что нить не дает двигаться вдоль нити вниз . Со стороны нити на шарик действует сила
(рис. 1.10 б) , шарик не двигается, потому что нить не дает двигаться вдоль нити вниз . Со стороны нити на шарик действует сила 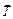
Если связь ограничивает движение тела в пространстве, то связь с телом взаимодействует. Мерой этого взаимодействия является сила реакции связи.
Сила, с которой связь действует на несвободное тело, мешая ему двигаться, называется реакцией связи. Реакция связи направлена противоположно направлению, в котором связь не дает телу двигаться.
Не всегда удается спрогнозировать направление реакции связи, но есть такие связи, для которых это легко сделать (см. подразд. 1.4).
Дата добавления: 2016-03-15; просмотров: 977;
