Краткие исторические сведения

Лекции о статике

Данное учебное пособие предназначено для студентов направления «Инженерная механика». В первой части учебного пособия изложены основные положения статики твердого тела в соответствии с программой теоретической механики для высших технических заведений Украины и являются результатом многолетней преподавательской деятельности его авторов в Приазовском государственном техническом университете.

Материал расположен в такой последовательности, чтобы можно было воспользоваться пособием и при изучении курса по коротким программам. Дополнения позволяют расширить знания студентов разного уровня подготовки.

В первых шести темах решены основные задачи теоретического курса статики – это приведение разных систем сил к более простому виду и определение условий (уравнений) их равновесия.

Некоторые специальные вопросы, которые, с одной стороны, расширяют круг основных задач, которые решает «Статика» в направлении их реальности, с другой стороны, станут примером практического применения полученных положений для решения конкретных задач. Такими направлениями являются:

– расчет усилий в стержнях ферм (тема 7);

– учет сил трения скольжения и трения качения (тема 8);

– равновесие рычага, которое позволяет выяснить условия устойчивости конструкции при ее опрокидывании (тема 9);

– определение координат центра тяжести тела (тема 10).

Основной целью предложенных примеров и задач (использованных из известных источников) является иллюстрация методики преподавания и техническое применение полученных знаний. Поскольку базовые положения раздела сведены в таблицы, есть возможность использовать их как раздаточный материал для студентов.

Пособие может быть использовано для самостоятельного изучения основных положений, т. к. авторы руководствовались проблемным подходом, а после изложенных тем помещены вопросы для самоконтроля.

Краткие исторические сведения

Эпоху создания первых орудий производства и искусственных построек следует признать за начало накопления того опыта, который в дальнейшем в связи с необходимостью передачи этого опыта послужил основой для формулирования законов механики. Однако,в то время как геометрия и астрономия античного мира представ­ляли развитые научные системы, в области механики были известны лишь отдельные положения, относящиеся к наиболее простым случаям равновесия тел. Таким образом, ранее всех разделов теоретической механики зародилась «Статика». Этот раздел развивался в тесной связи со строительным искусством античного мира. Хотя первые дошедшие до нас письменные трактаты по «Статике» относятся к IV в. до н. э. (Архит из Тарента), но остатки древних вавилонских и египетских построек позволяют предполагать, что элементарные сведения о статике сооружений и о простейших машинах для перемещения и поднятия тяжестей появились уже за несколько тысяч лет до нашей эры. Название «Механика» впервые ввёл великий мыслитель и учёный древности Аристотель, ученик Платона, живший с 384 по 322 г. до нашей эры. Аристотель коснулся вопросов механики в трёх своих сочинениях: «Физика», «О небе» и «О возникновении и уничтожении». В сочинениях Аристотеля, носящих в основном философский, а не естественно научный характер, излагается учение о равновесии рычага и других машин. Во времена Аристотеля механика развивалась очень медленно.

Можно отметить только один случай очень быстрого, почти скачкообразного развития механики, связанный с именем величайшего механика всех времён и народов – сиракузского учёного Архимеда (287–212 гг. до н. эры.), который дал механике настоящее научное обоснование, включив её в область точных наук. В своих сочинениях Архимед изложил теорию равновесия рычага, находящегося под воздействием параллельных сил, создал учение о центре тяжести тел, а также исследовал равновесие тел, плавающих в жидкости. Сочинения Архимеда отличаются строгостью

своих выводов и изяществом метода. На протяжении почти двух тысяч лет после Архимеда не было учё ных такого большого значения. Примерно к началу IV в. до н. э. уже были известны простейшие законы сложения и уравновешивания сил, приложенных к одной точке вдоль одной и той же прямой. Особый интерес привлекала задача о рычаге, при помощи которого, по словам одного из учеников Аристотеля, «меньшее осиливает большее, маленькая тяжесть поднимает большую». Им были установлены правила сложения и разложения параллельных сил, дано определение центра тяжести ряда геометрических фигур и тел, открыты законы равновесия тел в жидкости. Свои теоретические знания в области механики Архимед применял к различным практиче­ским вопросам строительства и военной техники.

В отличие от более ранних сочинений работы Архимеда лишены каких-либо натурфилософских элементов. Несмотря на то, что появление работ по статике было вызвано техническими потребностями, сочинения Архимеда лишены видимой связи с практикой. По своему характеру они абстрактны и очень похожи на «Начала» Евклида. Архимеду, прежде всего, принадлежит установление понятия центра тяжести тел, которое он сформулировал в сочинении, не дошедшем до нашего времени. Судя по более поздним источникам, Архимед так определил центр тяжести: «Центром тяжести некоторого тела является некоторая, расположенная внутри него точка, обладающая тем свойством, что если за нее мысленно подвесить тяжелое тело, то оно останется в покое и сохраняет первоначальное положение». В дошедших до нас сочинениях Архимеда по статике «О равновесии плоских фигур или о центрах тяжести плоских фигур» и «Послании к Эратосфену о механических теоремах» он развивает теорию нахождения центра тяжести различных фигур.

Потребности в создании различного рода технических устройств (строительных, военных и т.д.) выдвигали на первый план вопросы статики. Архимед, создав теорию рычага, заложил основы статики. Известно его знаменитое высказывание:«Дайте мне точку опоры, и я сдвину Землю».Строительная и военная техника основывалась на рычаге, позволявшем перемещать в пространстве тела большого веса при относительно небольших усилиях. Проблема рычага явилась обобщением эмпирически освоенных приемов его использования в разных областях деятельности. В своих трудах Архимед изложил основные постулаты теории рычага:

– равные тяжести на равных длинах уравновешиваются, на неравных же длинах не уравновешиваются, но перевешивает тяжесть на большей длине;

– если при равновесии тяжестей на каких-нибудь длинах к одной из тяжестей будет что-то прибавлено, то они не будут уравновешиваться, но перевесит та тяжесть, к которой было прибавлено;

– точно так же, если от одной из тяжестей будет отнято что-нибудь, то они не будут уравновешиваться, но перевесит та тяжесть, от которой не было отнято;

– если две величины уравновешиваются на каких-нибудь длинах, то на тех же самых длинах будут уравновешиваться и равные им.

Исходя из этих, многократно проверенных на практике, постулатов, Архимед формулирует закон рычага в виде следующих теорем:

– соизмеримые величины уравновешиваются на длинах, обратно пропорциональных тяжестям;

– если величины несоизмеримы, то они точно так же уравновесятся на рычагах, которые обратно пропорциональны этим величинам.

Дав определение центру тяжести тела как расположенной внутри его точки, при подвешивании за которую оно останется в покое и сохранит первоначальное положение, Архимед определил центры тяжести треугольника, параллелограмма, трапеции и других фигур.

Применив математику для изучения механического равновесия, Архимед показал, что математический подход к решению физических проблем не только помогает проникнуть в суть законов природы, но обогащает и саму математику.

Значительный вклад в развитие статики внес Иордан Неморарий – механик и математик XIII века. В трактате «О тяжестях» он вводит понятие момента силы для изучения неравноплечего рычага. Основная идея Неморария заключалась в том, что он установил разницу между весом тела P («pondus») и тяжестью тела G («gravitas»). Неморарий считал, что вес имеет постоянную величину, а тяжесть тела зависит от положения тела. То есть груз тяжелее, если в заданном положении линия его спуска менее наклонена.

Неморарий позднее понял, что известный у античных механиков закон рычага и неизвестный ему закон равновесия на наклонной плоскости является случаем части какого-то общего закона. Теория равновесия «простых» машин в школе Неморария опиралась на принцип сравнения относительной тяжести грузов при возможных перемещениях машины. Вообще, по своему содержанию трактаты И. Неморария – это следующий шаг на пути к развитию кинематического направления в статике, то есть к принципу возможных перемещений.

Величайшим деятелем эпохи Возрождения был знаменитый художник и выдающийся естествоиспытатель Леонардо да Винчи (1451–1519 гг.). С его именем связаны крупные открытия в области механики. Ему принадлежит первая формулировка правила параллелограмма сил в применении к частному случаю равновесия груза, располо­женного на наклонной плоскости. Это правило, доказанное в дальнейшем для взаимно перпендикулярных сил голландским ученым Стевином (1548–1620 гг.), а в общем случае как угодно направленных сил – французским ученым Робервалем (1602–1675 гг.), легло в основу современной статики.

При рассмотрении равновесия рычага Леонардо да Винчи пользуется понятием момента силы, причем кратчайшее расстояние от точки опоры до линии действия силы, то есть плечо силы, называет «потенциальным рычагом». В творчестве Леонардо механика занимала важное место в его заметках; имеется много рассуждений, касающихся теоретической и практической механики. Много внимания уделял вопросам строительной механики – теории арок, сводов и купольных перекрытий. Один из первых определил коэффициент трения. Большую часть его заметок составляют гидротехнические проекты. Известны его исследования механики движений человека и полета птиц. Использовал понятие момента, исследовал понятие силы, сложения сил, действующих на тело. В области механики Леонардо, как и его предшественники, прежде всего, обращается к закону равновесия рычага. Этот закон он формулирует на основе целой серии экспериментов, которые рассматриваются как промежуточная стадия работы, после чего становится возможным теоретическое обоснование Леонардо, осуществляет его, опираясь на понятие «веса в соответствии с положением» школы Иордана Неморария. Что касается строгости и логической стройности, то доказательство Леонардо значительно уступает формулировкой его предшественников; как и все подобные рассуждения, оно отражает присущий Леонардо инженерный подход к рассматриваемым явлениям. Его обоснование в физическом аспекте намного конкретнее и свидетельствует о реальном понимании реального рычага. С помощью сформулированного правила Леонардо решает задачи как для линейного, так и для ступенчатого рычага. В более поздних заметках он связывает правило рычага с понятием центра тяжести тела или системы тел, проявляя глубокое понимание архимедовой теории равновесия плоских фигур. Следует упомянуть, что им внедрено понятие «потенциального» плеча, под которым Леонардо понимал величину перпендикуляра, опущенного из точки опоры на направление силы. Эти представления можно, однако, с осторожностью, считать зарождением понятия момента силы относительно неподвижной точки. Опираясь на результаты своих экспериментов с полиспастами и другими сочетаниями подвижных и неподвижных блоков, Леонардо пытался сформулировать правило соотношения сил и скоростей перемещения груза в точки приложения силы тяги, т. е. определенной степени вариант «золотого правила» механики.

Родоначальником современной статики стал знаменитый голландский математик, физик и инженер Симон Стевин (1548–1620 гг.), который в 1586 году сформулировал закон сложения сил, или правило параллелограмма, и применил его при решении ряда задач. Он был известен современникам своими работами во многих областях науки, был автором труда «Начала статики». Он писал об устойчивом и неустойчивом равновесии. Симон Стевин ввел понятие метацентрадля расчета равновесия плавающих тел и использовалматематику длявычисления центров тяжести.

В результате проводимых исследований он открыл гидростатический парадокс. Стевин доказал, что давление жидкости на дно сосуда не зависит от формы сосуда, а только лишь от уровня жидкости. Стевин сформулировал закон гидростатического давления, он показал, что давление в жидкости одинаково во всех направлениях.Симон Стевин сумел объяснить, почему уровень жидкости в сообщающихся сосудах одинаков.

Самые важные открытия Стевина принадлежали механике, и именно статике и гидростатике, получившим в них приобретения, едва ли не первые со времени Архимеда по своей значительности. Первая была обязана ему открытием закона равновесия на наклонной плоскости, изложенным в сочинении «De Beghinselen der Weeghconst» (Лейден, 1586 г.) и тут же приведшим автора к теореме о равновесии трех сил, параллельных и пропорциональных трем сторонам какого-нибудь треугольника. Стевин первый дал такого рода условие равновесия блока, Галилей дополнил исследования Стевина рассуждением о равновесии груза на наклонной плоскости и высказал известное «золотое правило механики», согласно которому «что выигрывается в силе, то теряется в скорости».

Выдающимся открытием Стевина в гидростатике был закон пропорциональности давления, оказываемого жидкостью на дно сосуда, приводящий к выводу, что жидкость может оказывать на дно сосуда давление, превосходящее ее вес, т. е. так называемому гидростатическому парадоксу, который затем совершенно неправильно приписан Паскалю.

Стевин исследовал также и боковое давление жидкостей, причем употребил метод, составленный по образцу методов Архимеда и имеющий чрезвычайно важное значение. Стевин занимается исследованиями, относящимися к системам блоков, к веревочным многоугольникам и к равновесию кораблей. В последней своей работе пришел к заключению, что центр тяжести корабля располагается ниже центра тяжести вытесненной воды. С помощью мысленного эксперимента он доказал закон равновесия тел на наклонной плоскости. Это доказательство было основано на предположении, что вечное движение невозможно. Так еще в начале ХVII века Симон Стевин убедительно объяснил, что вечный двигатель не может существовать.

Из рассмотрения равновесия цепочки на наклонной плоскости Стевин вывел закон сложения действующих сил и закон разложения силы на составляющие, т. е. он вывел правило векторного сложения сил (для частного случая перпендикулярных сил). Симон Стевин предложил способизображения силс помощью линий.

В геометрическую статику большой вклад внес французский учёный Пьер Вариньон (1654–1722 гг.) Вариньон установил в окончательном виде понятие момента силы относительно точки и предложил геометрическое доказательство теоремы о том, что момент равнодействующей двух сходящихся сил равен сумме моментов составляющих сил (теорема Вариньона). В своей работе «Проект новой механики» (1687 г.) Вариньон, пользуясь этой теоремой, а также методом сложения и разложения сил, даёт строгую статическую теорию простейших машин. В этой работе статика твёрдого тела получила почти полное завершение. Основные работы относятся к геометрии и статике. Исходя из теории сложных движений сформулировал (около 1710 г.) закон параллелограмма сил. Его трактат «Новая механика, или статика», проект которого был опубликован в 1686 г., был издан посмертно в 1725 году в Париже. Установил (1687 г.) теорему о скользящих векторах для случая сходящейся системы сил. Одним из первых начал пользоваться математическим анализом.

Наиболее ярким представителем новой французской механики был Луи Пуансо(1777–1859 гг.). Основным его произведением является книга «Начала статики», выпущенная в 1802 году и переиздававшаяся многократно (10-е издание вышло в 1861 г.). В статике это произведение сыграло ту же роль, что «Начала» Ньютона в динамике. Здесь указывается на основное понятие, которое имеется о телах, – это то, что для существования в них не предполагается необходимости движения. И если возможно, что во Вселенной не найдется ни одной молекулы, которая находилась бы в абсолютном покое даже в очень короткий промежуток времени, тем не менее, совершенно ясно, что тело может существовать, находясь в покое. Но если это тело будет в покое хотя бы одно мгновение, то оно всегда таким и останется, если только какая-нибудь посторонняя причина не выведет его из этого состояния. Эту причину, какой бы она ни была и которая известна только по ее действиям, называют силой, или мощностью. Итак, сила есть какая-то причина движения. Л. Пуансо указывает, что сила обладает точкой приложения, величиной и направлением, и формулирует основные задачи механики: найти движение, которое какая-либо механическая система получает под действием заданных сил, и обратно: найти соотношения сил, действующих на систему, чтобы она получила заданное движение. Но для решения этой общей задачи нужно начать с частного случая – решить, какими должны быть соотношения сил, приложенных к системе, чтобы она получила движение, равное нулю, иными словами, находилась бы в равновесии. Если эта задача будет решена, то к ней легко будет привести и другую – вот почему обычно изучение механики начинают со статики, которую определяют как науку о равновесии сил. После этого наступает черед другой науки, которая рассматривает все вопросы, касающиеся движения тел; она называется динамикой, или наукой о движении.

Основное отличие статики от динамики заключается в том, что в решении статических задач достаточно знать только величины и направления приложенных сил, тогда как в динамике требуется, кроме того, знание и некоторых дополнительных данных. В то время кинематика еще не существовала как самостоятельная наука и Л. Пуансо считает возможным установить различие между равновесием и покоем в том, что на покоящееся тело не действуют никакие силы, тогда как в равновесии на тело действуют взаимоуничтожающиеся силы. Он не считает это различие существенно важным, что позволяет ему установить следующую аксиому: состояние тела, находящегося в покое или подверженного действию некоторых сил, не изменится, если предположить, что к этому телу приложены какие угодно новые силы, которые взаимно уравновешиваются между собой. Когда рассматривается равновесие свободного твердого тела, то достаточно знать лишь координаты точек приложения сил, величины сил и направляющие косинусы линий их действия; объем и форма рассматриваемого тела уже значения не имеют.

Если это тело не является свободным, то его всегда можно сделать таковым, отбросив сопротивления и заменив их подходящими силами. Таким образом, Л. Пуансо вводит в науку понятие о реакции связей и так называемую аксиому связей. В этом заключается отличие статики Пуансо от статики Лагранжа. Если на тело действует система сил, находящихся взаимно в равновесии, то можно считать, что одна из них уравновешивает все остальные, вместе взятые. Если приложить к телу одну силу 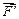, равную и прямо противоположную 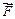, то силы 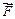и 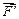взаимно уравновесятся. Поскольку же 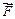уравновешивается со всей системой приложенных сил, то сила 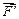' и совокупность всех остальных сил являются эквивалентными друг другу. Таким образом, можно сформулировать общий признак эквивалентности двух систем сил: они эквивалентны, если каждая из них в отдельности может быть уравновешена одной и той же третьей системой сил. Л. Пуансо рассматривает только частный случай эквивалентности, когда эта третья система представляет единственную силу. Этим Л. Пуансо вводит понятие о равнодействующей данной системы сил и об операциях сложения и разложения сил. В 1804г. появилось сочинение Л. Пуансо «Элементы статики», в котором излагается стройная система геометрической статики. В этой работе Л. Пуансо устанавливает понятие пары сил, разрабатывает теорию пар и затем применяет эту теорию к решению в общем случае задачи о приведении к простейшему виду системы сил, приложенных к твёрдому телу, и к выводу условий равновесия твёрдого тела. Л. Пуансо формулирует Основную теорему статики (теорему Пуансо). Л. Пуансо используется такой термин, как «вектор». Этот термин впервые придумал Гамильтон в 1847 году.

Основоположником аналитической статики является великий французский математик и механик Жозеф Луи Лагранж (1736–1813 гг.). В механике Лагранж выполнил работу по систематизации полученных результатов и по их обоснованию. В основу статики Лагранж положил принцип возможных перемещений. В классическом трактате «Аналитическая механика» (1788 г.) Лагранж в основу всей статики положил «общую формулу», являющуюся принципом возможных перемещений, а в основу всей динамики – «общую формулу», являющуюся сочетанием принципа возможных перемещений с принципом Даламбера.

Из «общей формулы» динамики может быть получена, как частный случай, «общая формула» статики. В разделе «Статика» первого тома «Аналитической механики» Лагранж, излагая теорию равновесия несвободной системы, использует принцип возможных перемещений в аналитической форме, аналогичной той, которую ранее уже использовал для отдельной частицы Клеро в теории равновесия вращающейся жидкости. Эта форма уравнения равновесия носит у Лагранжа наименование «общей формулы статики». Подавляющее большинство разрешаемых Лагранжем задач отражает технические проблемы того времени. Задачи эти относятся к вопросам равновесия тел, связанных между собой нерастяжимыми и растяжимыми нитями и стержнями, равновесия упругих нитей и пластин, статики несжимаемой и сжимаемой жидкости.

Жан Лерон Д'Аламбер (1717–1783 гг.) решает задачи статики на основе «Принципа сложения движений», который представляет собой закон сложения скоростей и сил по правилу параллелограмма. Даламбер не указал, как выбирать форму условий равновесия, заключающихся в его принципе; в отдельных случаях им применялись то принцип рычага, то правило параллелограмма сил.

Принципы «равновесия» сформулированы в виде следующей теоремы: «Если два тела движущихся со скоростями, обратно пропорциональными их массам, имеют противоположные направления, так что одно тело не может двигаться не трогаясь с места, то эти тела будут находиться в состоянии «равновесия». Во второй части «Трактата» Даламбер предложил общий метод составления дифференциальных уравнений движения любых материальных систем, основанный на сведении задачи динамики к статике. Он сформулировал правило для любой системы материальных точек, названное впоследствии «Принципом Даламбера», согласно которому, приложенные к точкам системы силы можно разложить на «действующие», то есть такие, которые вызывают ускорение системы, и "потерянные", необходимые для равновесия системы. Даламбер считает, что силы, которые соответствуют «потерянным» ускорениям, образуют такую совокупность, которая никак не влияет на фактическое поведение системы. Следует отметить, что сам Даламбер при изложении своего принципа не прибегал ни к понятию силы (считая, что оно не является достаточно четким, чтобы входить в перечень основных понятий механики), ни тем более к понятию силы инерции.

Дальнейшее развитие аналитической статики связано с именем великого украинского математика и механика М. В. Остроградского (1801–1862 гг.). Академик является крупнейшим представителем аналитического направления в механике и родоначальником русской школы аналитиков – механиков. Его главнейшие работы относятся к аналитической механике и её основным принципом. Так, принцип возможных перемещений Остроградский обобщил на случай так называемых неудерживающих связей, то есть связей, которые выражаются математическими неравенствами.

Михаилу Ломоносову(1711–1765 гг.) и Леонарду Эйлеру (1707–1783 гг.) мы обязаны тем, что Российская Академия вскоре после своего создания стала крупнейшим мировым центром науки и послужила расцвету русской науки в

послепетровский период. Характерное для петровской эпохи бурное развитие техники – гигантский рост добычи металлов, строительство флота, городов и крепостей, возросшие требования к кораблевождению и баллистике – вызвало появление первых на русском языке руководств по механике (Г. Г. Скорняков-Писарев, «Наука статическая или механика», 1722 г. и др.). В результате деятельности М. Ломоносова и Л. Эйлера появились первые русские ученые, творчески овладевшие методами механики и способствовавшие ее дальнейшему развитию. Среди этих ученых должен быть отмечен ученик Л. Эйлера и М. Ломоносова, академик С. К. Котельников (1723–1808 гг.), выпустивший в 1774 г. трактат по механике под названием «Книга, содержащая в себе учение о равновесии и движении тел». В этой книге приводятся основные сведения из области статики твердых и частично гибких и упругих тел (нитей, канатов, балок и др.), а статика простейших машин и механизмов с учетом сил трения и прочно­сти деталей сооружений. С. К. Котельников вел большую преподавательскую работу; благодаря предпринятой им широкой пропаганде механических знаний число образованных русских механиков и инженеров быстро росло; к концу XVIII в. Россия не уступала по уровню механического образования западноевропейским странам.

Развитию механики в России на рубеже XVIII—XIX вв. много способствовал академик С. Е. Гурьев (1766–1813 гг.). С. Е. Гурьеву принадлежат обширный труд «Основания механики», первая часть которого была опубликована в печатном виде после смерти автора в 1815 году, и ряд сочинений, содержащих решение отдельных конкретных задач статики и динамики.

В обосновании аксиоматики статики большую роль сыграли Н. Е. Жуковский (1847–1921 гг.), С. А. Чаплыгин (1869–1942 гг.), В. Г. Имшенецкий (1832–1892 гг.), О. И. Сомов (1815–1876 гг.). Большой вклад в развитие графостатики внес В. Л. Кирпичёв (1845–1913 гг.).

Как следует из краткого исторического очерка раздел теоретической механики «Статика» со времен основателя геометрической статики Архимеда, получил развитие в аналитическом виде, так как инженерная практика активизировала развитие точной математической теории в области механики деформируемого твердого тела. В ХIХ веке сформировались основы таких наук как: сопротивление материалов, строительная механика, теория упругости, контактные задачи теории упругости, механика машин, теория пластин и оболочек.

Показательным для Украины является то, что в 1919 г. была создана Академия наук Украины вместе с Институтом технической механики. Перечислим некоторых ведущих украинских ученых, которые развили многие отрасли механики деформируемого твердого тела на основе знаний, связанных с разделом «Статика»: Тимошенко С. П., Динник А. Н., Коваленко А. Д., Кильчевский Н. А., Писаренко Г. С., Савин Г. Н., Панасюк В. В. и др.