I уровень. Теоретические сведения
§ Дисперсия света – зависимость абсолютного показателя преломления вещества от частоты света. Вследствие дисперсии света узкий пучок белого света, проходя сквозь призму из стекла или другого прозрачного вещества, разлагается в дисперсионный спектр, образуя радужную полоску.
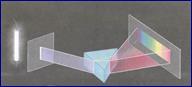
§ Спектр оптический – распределение по частотам (или длинам волн) интенсивности оптического излучения некоторого тела (спектр испускания) или интенсивности поглощения света при его прохождении через вещество (спектр поглощения). Различают спектры: линейчатые, состоящие из отдельных спектральных линий; полосатые, состоящие из групп (полос) близких спектральных линий; сплошные, соответствующие излучению или поглощению света в широком интервале частот.
§
§ Сплошной спектр. 
§ Линейчатые спектры.
§
Спектр ртути (Hg) 
Спектр гелия (He) 
Спектр водорода (H) 
Спектр неона (Ne) 
Спектр аргона (Ar) 
Спектр криптона (Kr) 
§ Спектроскоп. Для наблюдения спектров пользуются спектроскопом. Наиболее распространенный призматический спектроскоп состоит из двух труб, между которыми помещают трехгранную призму. В трубе 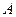 , называемой коллиматором, имеется узкая щель, ширину которой можно регулировать поворотом винта. Перед щелью помещается источник света, спектр которого необходимо исследовать. Щель располагается в фокальной плоскости линзы коллиматора, и поэтому световые лучи из коллиматора выходят в виде параллельного пучка. Пройдя через призму, световые лучи направляются в трубу , называемой коллиматором, имеется узкая щель, ширину которой можно регулировать поворотом винта. Перед щелью помещается источник света, спектр которого необходимо исследовать. Щель располагается в фокальной плоскости линзы коллиматора, и поэтому световые лучи из коллиматора выходят в виде параллельного пучка. Пройдя через призму, световые лучи направляются в трубу 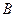 , через которую наблюдают спектр.» , через которую наблюдают спектр.»
| 
|
Расчет– «Тема: «Определение моментов инерции твердых тел с помощью крутильного маятника».
Расчетные формулы
1. Определение момента инерции твердого тела методом крутильных колебаний.
Как уже было сказано, крутильный маятник состоит из рамки, подвешенной на натянутой стальной нити и жестко закрепленного в ней твердого тела – рис 4,5. Период колебаний крутильного маятника равен
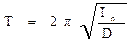 ,
,
где In – момент инерции маятника относительно n = 1,2; D – постоянная момента упругих сил стальной нити.
Момент инерции маятника равен сумме момента инерции I0 рамки и момента инерции исследуемого тела Iт
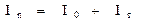 .
.
Если колеблется свободная рамка без тела, то её период колебаний:
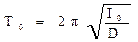 . (3)
. (3)
Таким образом, период колебаний крутильного маятника:
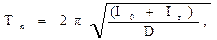 (4)
(4)
Если момент инерции рамки I0 известен, то решая совместно уравнения (3) и (4), получаем формулу для экспериментального определения моментов инерции исследуемых тел (рис. 6) методом крутильных колебаний:
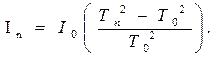 (5)
(5)
Период колебаний маятника для различных вариантов эксперимента определяется по формуле
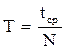 , (6)
, (6)
где N – число колебаний; tср – время N колебаний.
2. Расчет момента инерции твердого тела согласно формуле (1) .
Момент инерции сплошного цилиндра относительно оси n определяется согласно выражению
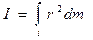 ,
где ,
где 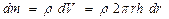 (рис. ): ρ – плотность цилиндра.
Таким образом, момент инерции сплошного цилиндра относительно оси 1: (рис. ): ρ – плотность цилиндра.
Таким образом, момент инерции сплошного цилиндра относительно оси 1:
| 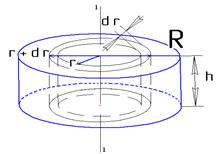 Рис. 4
Рис. 4
|
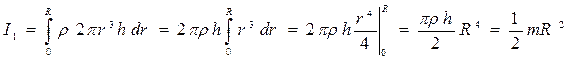 . (7) »
. (7) »
Компьютерное моделирование, расчет.
Тема: «Масс-спектрометрический метод определения удельного заряда частиц»
СХЕМА РАБОТЫ МАСС СПЕКТРОМЕТРА (рис.3). Проба исследуемого вещества подается в вакуумную камеру через входное отверстие. Сразу за входным отверстием поступающий газ ионизируется пучком электронов, идущих с анода ионизатора. Далее ионизированный газ проходит через мощное постоянное магнитное поле, которое отклоняет траектории движения ионизированных частиц газа. Ионы с более высоким отношением массы к заряду отклонятся на меньший угол вследствие своей большей инертности при одинаковой величине воздействия. В итоге газ разделяется на потоки по критерию величины отношения массы к заряду, то есть по химическому составу. Величины этих потоков регистрируются на коллекторах ионов на приемной поверхности вакуумной камеры. По показаниям счетчиков определяют процентное соотношение того или иного компонента.
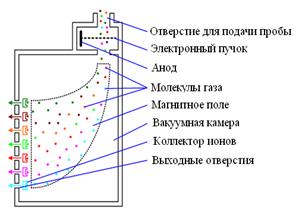 Рис.3. Схема работы масс-спектрометра.
Рис.3. Схема работы масс-спектрометра.
| 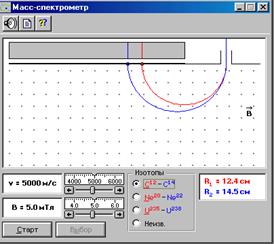 Модель масс-спектрометра для проведения компьютерных исследований показана на рис. 5.
Модель масс-спектрометра для проведения компьютерных исследований показана на рис. 5.
|
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:
1. Подведите маркер мыши к движку регулятора величины магнитной индукции, нажмите левую кнопку мыши и, удерживая ее в нажатом состоянии, двигайте движок, установив числовое значение В, указанное для таблиц 1- 4.
2. Аналогичным образом, зацепив мышью движок регулятора скорости, установите минимальное значение 1000 м/с.
3. Нажмите мышью кнопку «Изотопы С12-С14»
4. Нажмите мышью кнопку «Старт» и синхронно секундомер. Проследите за движением двух изотопов в магнитном поле модельного масс-спектрометра и по секундомеру определите время t этого движения.
5. Запишите в таблице значения радиусов окружностей, по которым двигались эти изотопы (они показаны красным и синим цветом в правом углу окна) и время движения изотопов в вакуумной камере масс-спектрометра.
6. Последовательно увеличивая скорость частиц на 1000 м/с, проделайте п.п. 4-5 ещё 9 раз и заполните таблицу 1.
7. Нажмите мышью кнопку «Изотопы Ne20-Ne22 », проведите измерения п.п. 4-6. Заполните таблицу 2.
8. Проведите аналогичные измерения с изотопами урана. Заполните таблицу 3
9. Проведите измерения согласно п.п. 4-5 для неизвестного химического элемента. Проведите расчеты и заполните таблицу 4.
10. Определите молярную массу изотопов неизвестного элемента по формуле
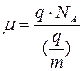 ,
,
где q/m – удельный заряд, рассчитанный по формуле (4); q = 1,6·10-19 Кл; NА = 6,02·1023 моль-1 – число Авогадро.
11. По молярной массе μ в таблице Менделеева найдите химический элемент Х. Запишите химические формулы изотопов Х1 и Х2 в таблице 4.
Таблицы 1. Результаты измерений и расчётов
В = 5 мТл
| v×103,м/с | ||||||||||||
| R1, см (С12) | ||||||||||||
| t, с (С12) | ||||||||||||
| R2, см (С14) | ||||||||||||
| t, с (С14) | ||||||||||||
| q1/m1, Кл/кг q2/m2, Кл/кг | ||||||||||||
| Табличные значения: q1/m1 = 0,80·107 Кл/кг q2/m2 = 0,69·107 Кл/кг | ||||||||||||
и т.д. »
Практическое задание.
При изучении методов научного познания привести примеры их применения в процессе проведения методических, научных и научно-методических мероприятий.
Дата добавления: 2016-03-05; просмотров: 2165;
