Приведение системы сходящихся сил к более простому виду

Пусть на твердое тело действует система сил 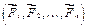которые приложены в точках 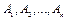соответственно (рис.2.1 а). Действующая система сил является сходящейся, так как линии действия всех сил пересекаются в одной точке – точке О. Поскольку сила – это скользящий вектор, перенесем все силы в точку О. Таким образом, мы получили систему сил, приложенных в одной точке. Она эквивалентна заданной системе сил.

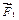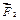На основе аксиомы параллелограмма сил (Дополнение А.2) проведем последовательное сложение сил. Сначала сложим силы и , находим равнодействующую 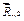(рис. 2.1 б)

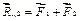. (2.1)

Дальше складываем 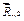и 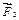(строя опять треугольник этих сил) и находим равнодействующую 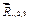. Продолжая сложение, дойдем до последней силы и получим

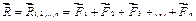, (2.2)

то есть вместо системы n сил, которая действовала на твердое тело, мы получили одну силу 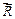, действие которой эквивалентно исходной системе сил (рис. 2.1 в).

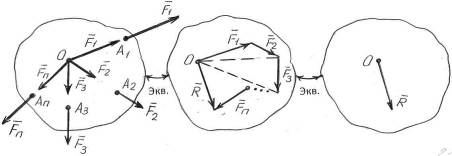
а б в

Рисунок 2.1

Таким образом, систему сходящихся сил можно заменить одной силой - равнодействующей:

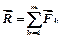.(2.3)

Равнодействующую можно определить двумя способами, геометрическим и аналитическим, так же как главный вектор.(1.2, п. 5).