ИНТЕГРАЛЬНАЯ ТЕОРЕМА КОШИ

Теорема коши. Если функция аналитична в области G, то интеграл по любому замкнутому контуру равен нулю, т.е.

.

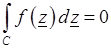Следствие. Интеграл по всякой дуге, находящейся в области аналитичности функции , зависит только от положения начальной и конечной точек этой дуги и, следовательно, одинаков для всех дуг, имеющих одинаковые начальную и конечную точки. Другими словами, интеграл от не зависит от пути интегрирования.

Действительно, если дуг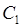и и 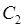имеют общую начальную точку 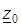и конечную точку 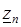(рис. 3.11), то интеграл

.

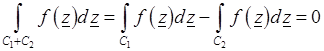Откуда следует, что

.

ФОРМУЛА КОШИ

Предположим, что функция 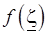является аналитической в односвязной области G плоскости 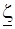, а также на контуре Г, ограничивающем эту область. Пусть 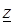– любая точка внутри области G (рис. 3.12).

Тогда для любой точки 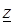области G справедливо равенство

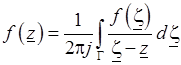, (3.10)

называемое формулой Коши. Величина, стоящая в правой части формулы (3.10), называется интегралом Коши. Для вычисления его необходимо знать значения функции 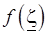только на контуре Г. Следовательно, формула Коши позволяет находить значения аналитической функции в любой точке, лежащей внутри области G, если известны значения этой функции на контуре Г.