НУЛИ И ОСОБЫЕ ТОЧКИ

Если в точке 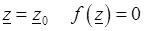, то эта точка называется нулем функции.

Точка, принадлежащая области аналитичности G, называется изолированной особой точкой, если вокруг нее можно описать круг, не содержащий других особых точек. Например, функция

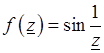
имеет в точке 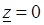изолированную особую точку, так как в ней не определена, но в любой ее окрестности эта функция является аналитической.

В основу классификации изолированных особых точек может быть положен вид разложения функции в ряд Лорана в окрестности особых точек. Изолированная особая точка 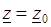называется:

1) устранимой, если существует конечный предел

;

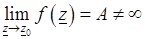2) полюсом, если

;

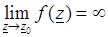3) существенно особой точкой, если не существует .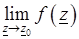

ПОНЯТИЕ О ВЫЧЕТЕ

Вычетом функции в изолированной особой точке 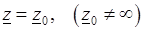называется величина

,

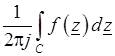где C – достаточно малая окружность, такая, что в описываемом ею круге нет других особых точек, кроме 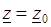. Величина вычета не зависит от радиуса. Обход контура C ведется против часовой стрелки.

Обозначается вычет функции в точке 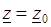следующим образом: 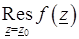. Как видно из формулы (3.13), при следует, что

,

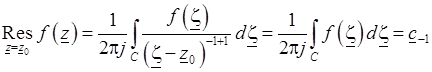где 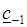– коэффициент ряда Лорана при .

Если особая точка 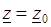является устранимой, то вычет в ней равен нулю.

Дадим определение вычета в бесконечно удаленной точке. Пусть в окрестности точки 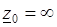функция допускает разложение в ряд Лорана

.

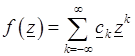Тогда вычет в бесконечно удаленной точке определяется формулой

,

где С – окружность достаточно большого радиуса, обход которой выполняется по часовой стрелке (бесконечно удаленная точка остается слева). При этом вне этой окружности не должно быть других особых точек функции , отличных от бесконечно удаленной точки.

ТЕОРЕМА О ВЫЧЕТАХ

С помощью вычетов можно значительно облегчить вычисление интегралов от функций комплексного переменного. Следующая теорема показывает, как это можно сделать.

Пусть 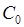– простой замкнутый контур, на котором функция аналитична всюду, за исключением n изолированных особых точек 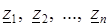внутри круга.

Тогда интеграл функции комплексного переменного

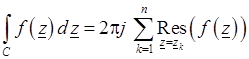. (3.17)