РАЗЛОЖЕНИЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ В РЯД
Ряды вида
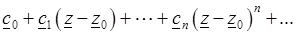 (3.11)
(3.11)
называются степенными.
3.11.1 РЯД ТЕЙЛОРА
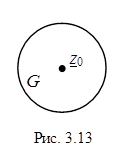 Пусть функция
Пусть функция  однозначная и аналитическая внутри ограниченной области G с центром в точке
однозначная и аналитическая внутри ограниченной области G с центром в точке 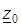 (рис. 3.13).
(рис. 3.13).
Тогда во всякой точке 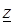 , находящейся внутри круга G, функция
, находящейся внутри круга G, функция  может быть представлена с помощью степенного ряда (3.11), коэффициенты которого вычисляются по формулам
может быть представлена с помощью степенного ряда (3.11), коэффициенты которого вычисляются по формулам
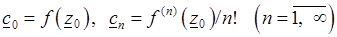 .
.
В развернутой форме ряд имеет следующий вид:
 (3.12)
(3.12)
Пример 3.4. Разложить в ряд  в окрестности точки
в окрестности точки  .
.
Поскольку
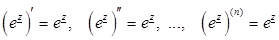 ,
,
то в соответствии с (3.12)
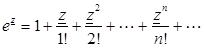
3.11.2. РЯДЫ ЛОРАНА
 Пусть функция
Пусть функция  является однозначной аналитической внутри кольца между концентрическими окружностями
является однозначной аналитической внутри кольца между концентрическими окружностями 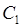 и
и 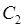 с центром в точке
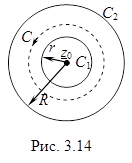
с центром в точке 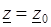 (рис. 3.14). Тогда функция
(рис. 3.14). Тогда функция  может быть представлена в этом кольце с помощью ряда Лорана
может быть представлена в этом кольце с помощью ряда Лорана
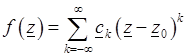 ,
,
где
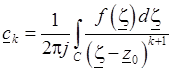
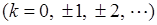 . (3.13)
. (3.13)
Здесь C – произвольно выбранный замкнутый путь интегрирования внутри кольца, по которому обходят точку 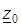 против часовой стрелки.
против часовой стрелки.
Часто разложение функции  можно получить, не прибегая к формуле (3.13) для вычисления коэффициентов
можно получить, не прибегая к формуле (3.13) для вычисления коэффициентов 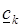 . В этих случаях используются свойства бесконечной геометрической прогрессии
. В этих случаях используются свойства бесконечной геометрической прогрессии
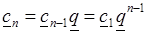 ,
, 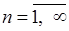 .
.
Как известно, при 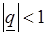 сумма этой прогрессии
сумма этой прогрессии
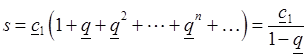 .
.
Пример 3.5.Разложить функцию
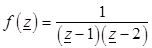 (3.14)
(3.14)
в кольце 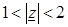 с центром в точке
с центром в точке  .
.
Функцию (3.14) можно представить в виде суммы дробей
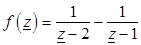 .
.
Разложим каждую дробь в отдельности в ряд. Преобразуем дробь 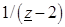 в выражение суммы бесконечной геометрической прогрессии со знаменателем
в выражение суммы бесконечной геометрической прогрессии со знаменателем 
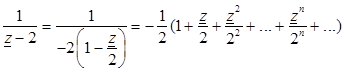 . (3.15)
. (3.15)
Аналогично поступим с дробью 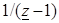
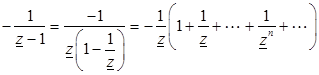 . (3.16)
. (3.16)
Складывая (3.15) и (3.16), получим искомый ряд для функции (3.14)
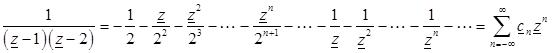 ,
,
где 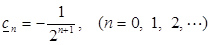 ,
, 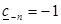
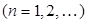 .
.
Дата добавления: 2016-02-14; просмотров: 944;
