КОМПЛЕКСНОГО ПЕРЕМЕННОГО. Пусть функция комплексного переменного определена и непрерывна на дуге C (рис
 Пусть функция комплексного переменного
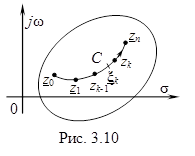
Пусть функция комплексного переменного  определена и непрерывна на дуге C (рис. 3.10). Разобьем дугу C на "элементарные" дуги и пронумеруем точки деления в направлении от начальной точки
определена и непрерывна на дуге C (рис. 3.10). Разобьем дугу C на "элементарные" дуги и пронумеруем точки деления в направлении от начальной точки 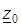 к конечной
к конечной 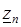 . Введем обозначения
. Введем обозначения
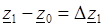 ,
, 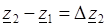 , ... ,
, ... ,
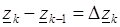 , ... ,
, ... , 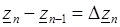 .
.
Число 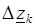 изображается вектором, идущим от точки
изображается вектором, идущим от точки 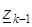 к
к 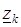 . Выберем по одной точке
. Выберем по одной точке 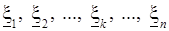 на каждой элементарной дуге. Составим сумму
на каждой элементарной дуге. Составим сумму
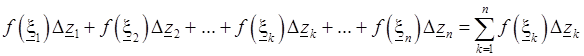 .
.
Предел этой суммы, вычисленной при условии, что 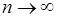 , а длина наибольшей из элементарных дуг
, а длина наибольшей из элементарных дуг 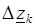 стремится к нулю, называется интегралом от функции
стремится к нулю, называется интегралом от функции  по дуге C и обозначается следующим образом:
по дуге C и обозначается следующим образом:
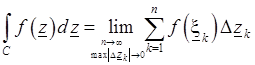 . (3.8)
. (3.8)
Вычисление интеграла (3.8) сводится к вычислению криволинейных интегралов от действительных функций. Пусть
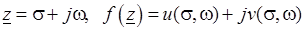 .
.
Тогда
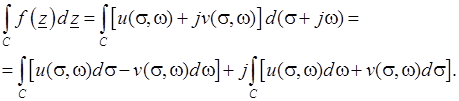
Свойства интеграла ФКП:
1. Для любых постоянных 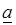 и
и 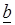 справедливо
справедливо
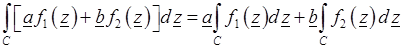 .
.
2. При изменении направления интегрирования знак интеграла меняется на обратный:
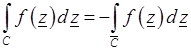 . (3.9)
. (3.9)
Здесь дуга 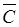 геометрически совпадает с дугой C, но имеет противоположное направление. Свойство (3.9) следует из уравнения (3.8), в правой части которого при замене направления интегрирования все
геометрически совпадает с дугой C, но имеет противоположное направление. Свойство (3.9) следует из уравнения (3.8), в правой части которого при замене направления интегрирования все 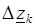 меняют свой знак.
меняют свой знак.
3. Если дуга состоит из дуг 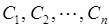 , то
, то
 .
.
Дата добавления: 2016-02-14; просмотров: 669;
