НЕПРЕРЫВНОСТЬ ФУНКЦИЙ

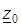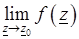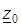Если функция определена в точке и в некоторой ее окрестности и предел не только существует, но и равен значению функции в точке , т.е.

,

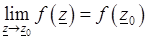то функция называется непрерывной в точке .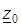

Функция непрерывна в области G, если она непрерывна в каждой точке этой области.

Для непрерывных ФКП справедливы все свойства непрерывных функций действительного переменного:

1. Сумма, разность, произведение и частное (если знаменатель не обращается в нуль) двух непрерывных функций есть функция непрерывная.

2. Непрерывная функция 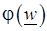от непрерывной функции 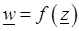является непрерывной.

ПРОИЗВОДНАЯ ФКП

Пусть функция 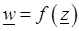определена и непрерывна в некоторой области Е. Рассмотрим две точк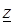и и 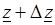, принадлежащие области Е, и составим отношение

.

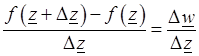Если существует предел отношения 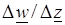при стремлении 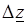к нулю по любому закону, то этот предел называется производной функции в точке 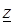и обозначается следующим образом:

.

Отметим, что требование существования предела отношения 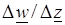и его независимости от закона стремления 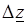к нулю накладывает на функцию более сильные ограничения, чем аналогичное требование для функции 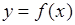действительного переменного .

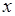Так, для того чтобы показать, что функция 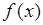имеет предел, достаточно доказать, что при приближении к точке 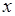слева и справа существуют пределы, и эти пределы равны. В случае функции комплексного переменного 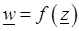требование существования производной означает существование предела отношения 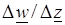при приближении к точке 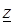по любому пути.

Поскольку определение производной ФКП совпадает с определением производной функции действительного переменного, то все правила дифференцирования функций действительного переменного применимы к ФКП.