Базисы представления переключательных функций

Функционально полные системы переключательных функций представляют собой базис. Всего можно получить 17 различных минимальных базисов из логических функций двух переменных.

Имеются функции, обладающие всеми пятью отмеченными свойствами. Таковы функции 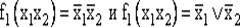(см. табл. 26). Часто их называют соответственно ИЛИ-НЕ, И-НЕ. Таким образом, это базисы, состоящие из одной функции (базис Вебба и базис Шеффера). Этот факт очень важен при технической реализации дискретных устройств: достаточно иметь элементы, реализующие только одну из этих функций, чтобы построить любую, сколь угодно сложную схему. Имеются базисы, состоящие из двух функций:

Иногда используется не минимальный базис — из трех функций:

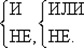
Имеется и довольно экзотический базис Жегалкина:

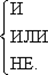
В дальнейшем нам пригодится так называемый импликативный базис:

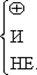
Если рассматривать переключательные функции большего числа аргументов, то можно поставить задачу отыскания базисов, не зависящих от некоторых модификаций соответствующих функций. Такие модификации могут быть, например, вызваны подстановкой констант 0, 1 и инверсией переменных, что происходит при некоторых отказах (дефектах) соответствующих логических элементов. Такие базисы называют толерантными. Например, переключательная функция четырех переменных 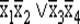— толерантный базис — функционально полная толерантная функция, которая при подстановке констант вместо переменных или при инверсии переменных модифицируется также в базисную функцию:

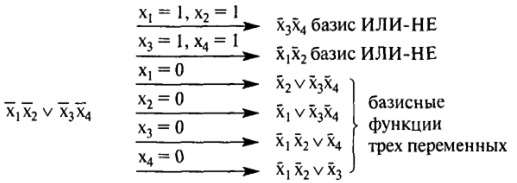
Пример анализа и определения свойств ПФ,
заданной десятичным номером

Дано; двоичная переключательная функция № 17410.

Получим соответствующий двоичный код: 101011102(27+ 25+ 23+ 22+ 21). Таблица истинности ПФ № 17410показана в табл. 29.

Таблица 29

Таблица истинности

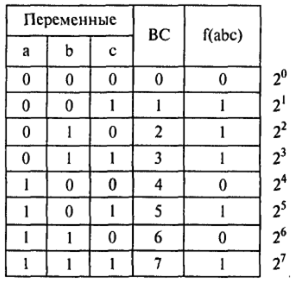
Получим восьмеричный код ПФ: 2568.

Получим шестнадцатеричный код ПФ: АЕ16.

Получим символическую форму: f ( abc )10= 1, 2, 3, 5, 7 [0, 4, 6].

В двоичном виде: f ( abc )2= 0012∨ 0112 ∨ 1012 ∨ 1112∨ 0102.

Определим свойства ПФ №17410.

1. Поскольку на наборе 000 ПФ равна 0, то ПФ обладает свойством сохранения константы «0»,

2. Поскольку на наборе Ш ПФ равна 1, то ПФ обладает свойством сохранения константы «1».

3. Рассмотрим все возможные линейные ПФ от трех аргументов в зависимости от значений коэффициентов полинома k 0⊕ k 1c ⊕ k 2b ⊕ k 3а (табл. 30).

Таблица 30