Бинарная дизъюнкция

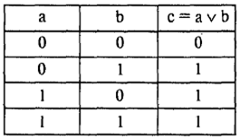
Дизъюнкция n переменных ложна тогда и только тогда, когда все составляющие ее переменные ложны.

Логическая операция, соответствующая частице «не», словосочетанию «неверно, что», называется инверсией . Пример инверсии: «Студент Петров не отличник», «Неверно, что студент Иванов является спортсменом».

Инверсией называется также переключательная функция (ПФ), полученная отрицанием данной ПФ.

Инверсию a обозначают 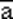, используя знак дополнения множеств.

Таблица истинности унарной операции инверсии В ↦ В имеет вид, представленный в табл. 18.

Таблица 18

Бинарная инверсия

Логическая операция, соответствующая союзу «если, ... то», называется импликацией .

Примеры импликации: «Если вы будете хорошо заниматься в семестре, то сдадите экзамен по дискретной математике».

Импликацией называется также логическая операция, соединяющая две переменных а и b в такую переключательную функцию c , которая равна 0 (ложна) только тогда, когда а истинно, а b ложно. Импликация обозначается символом →.

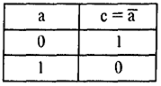
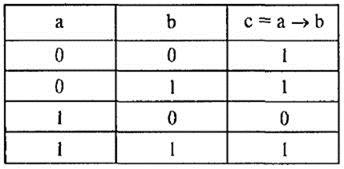
Таблица истинности импликации имеет вид, представленный в табл. 19.

Таблица 19

Импликация

Приведенное выше высказывание преподавателя будет расценено студентами как ложь, если они действительно хорошо занимались в семестре, а на экзамене получили неудовлетворительные оценки.

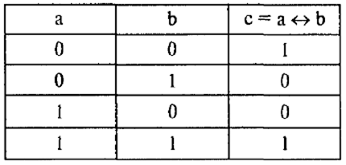
Логическая операция, соответствующая союзу «тогда и только тогда, когда», называется эквиваленцией (эквивалентностью).

Пример эквиваленции (эквивалентности): «Я поеду к морю тогда и только тогда, когда сдам экзамен по дискретной математике».

Эквиваленцией (эквивалентностью) называется также логическая операция, соединяющая две переменных в такую ПФ, которая истинна тогда, когда обе образующих ее переменных одновременно истинны или одновременно ложны. Эквиваленция обозначается символом ↔.

Таблица истинности эквиваленции имеет вид, представленный в табл. 20.

Таблица 20

Эквиваленция

Основные двоичные логические операции:

1) дизъюнкция ∨ («ИЛИ»);

2) конъюнкция & («И»);

3) инверсия, или отрицание ¯ («НЕ»);

4) импликация → («ЕСЛИ, ТО»);

5) эквиваленция ↔ («ТОГДА И ТОЛЬКО ТОГДА, КОГДА»).

Кроме того, имеется операция:

6) сумма по модулю 2 ⊕ («НЕВЕРНО, ЧТО ТОГДА И ТОЛЬКО ТОГДА, КОГДА» «ИЛИ-ИЛИ»).

Имеются также специальные операции:

7) стрелка Пирса ↓ («ИЛИ-НЕ»);

8) штрих Шеффера | («И-НЕ») и др.

Алгебра, несущим множеством которой является множество ПФ, а операциями — дизъюнкция, конъюнкция и инверсия, называется булевой алгеброй ПФ .

ПФ можно описать некоторые условия, например, равенства (неравенства) некоторых битов, значения отдельных битов 0 или 1, например:

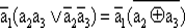
означает, что бит а1должен быть равен нулю и при этом биты а2и а3равны.

Решить логическое уравнение — значит определить значения переменных, при которых соответствующая ПФ = 1 (истинна), где 1 — константа.

Решить систему логических уравнений — значит определить значения переменных, при которых соответствующие ПФ = 1.

Пример. Дана таблица истинности для трех ПФ (табл. 22).

Таблица 22

Таблица истинности трех ПФ

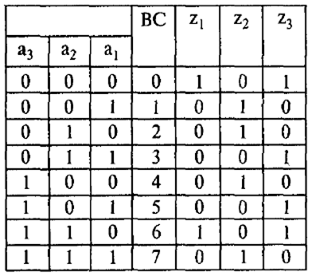
z1= 0, 6 [1, 2, 3, 4, 5,7];

z2= 1, 2, 4, 7 [0, 3, 5, 6] = a1⊕ a2⊕ a3= 1;

z3= 0, 3, 5, 6 [1, 2, 4, 7].

Здесь указаны номера наборов, на которых ПФ равны единице. Это так называемая символическая форма задания ПФ (СФ ПФ). Видно, что общих решений нет.

Если же взять

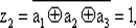
то получим

z2= 0, 3, 5, 6 [1, 2, 4, 7],

т. е. решение системы z1, z2, z3= 0, 6.

Если же в уравнении указывается равенство с другой переменной или функцией, то, как мы уже знаем из теории множеств:

a1⊕ a2⊕ a3= a3, a1⊕ a2⊕ a3⊕ a3= 0, a1⊕ a2= 0.V

Решение: 01, 10 á a 1a 2ñ .

Понятие о переключательных схемах и
технической реализации переключательных функций

Исторически первое практическое применение теория переключательных функций нашла в так называемых переключательных схемах (ПС, контактных схемах). Такие схемы построены на механических переключателях и реле (дистанционных переключателях), содержащих контакты двух типов: замыкающие, обозначаемые: 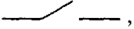и размыкающие, обозначаемые: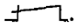

При этом параллельное соединение контактов соответствует дизъюнкции, а последовательное — конъюнкции.

Например, переключательная схема, реализующая импликацию x 1→ х2, представлена на рис. 29.

Такая схема проводит ток, если х2замкнут (сработал) или х1замкнут (не сработал).

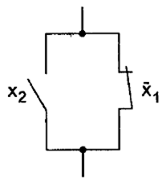
Рис. 29.Переключательная схема , реализующая импликацию x 1→ х2

Переключательная реализация функции 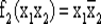представлена на рис. 30.

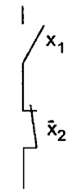
Рис. 30.Переключательная схема , реализующая импликацию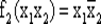

Предполагается, что контакты срабатывают, когда подается напряжение на обмотки соответствующих реле, не изображенных на рис. 29–30, или нажимаются соответствующие кнопки, включаются соответствующие тумблеры, и т. д.

Иногда с целью упрощения переключательные схемы изображают в виде только символов контактов (рис. 31).

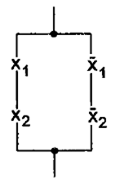
Рис. 31.Упрощенная переключательная схема эквиваленции x 1↔ х2

Таким образом, каждой такой последовательно-параллельной схеме можно поставить в соответствие некоторую переключательную функцию (формулу логики).

Переключательная схема — схема из замыкающих, размыкающих и переключающих контактов, показана на рис. 32.

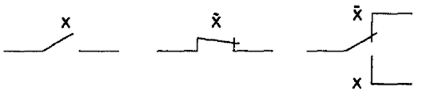
Рис. 32.Переключательная схема

Последовательно-параллельная контактная схема соответствует конкретной ПФ.

Упрощенная ПС изображается в символах переменных (рис. 33).

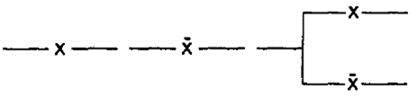
Рис. 33.Упрощенная переключательная схема

Применяя равносильные преобразования ПФ, можно упрощать ПС, уменьшая число контактов.

Возможна реализация ПФ схемами из функциональных элементов, программно. Техническая реализация базисных логических функций может быть основана на использовании различных физических явлений, например, базисы И-НЕ, ИЛИ-НЕ — явлений в полупроводниках, импликация — магнитных явлений.

В ряде случаев используются пневматическая реализация (струйные элементы), гидравлическая реализация, оптическая реализация.

Переключательные (логические) элементы изображают в виде прямоугольников, в которых инверсные входы и выходы изображают в виде кружков, а символы логических операций указывают в верхней части прямоугольника. Это условное графическое обозначение логических элементов ( рис. 34).

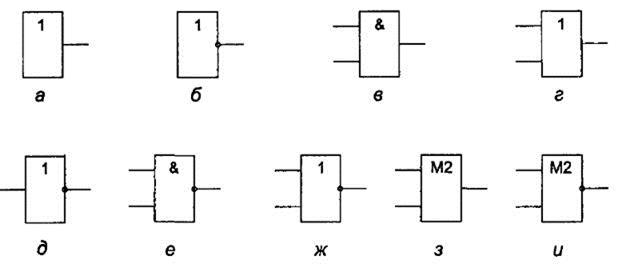
Рис. 34.Условное графическое обозначение логических элементов по стандарту РФ:

а — константа 1; б — константа 0; в — конъюнкция; г — дизъюнкция; д — инверсия;
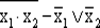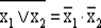e — ; ж — ; з — x 1⊕ х2; и —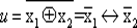

Путем соединения логических элементов получают схему, реализующую требуемую логическую функцию в виде суперпозиции базисных функций, каждая из которых реализуется определенным логическим элементом.

В электронных приборах конъюнкция и дизъюнкция реализуются соответственно последовательным и параллельным соединением ключевых полупроводниковых элементов, отрицание — включением нагрузки в коллекторную цепь транзистора. Так, переключательная функция 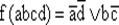реализуется, как показано на рис. 35.

Здесь кружки — это транзисторы, т. е. элементарные бесконтактные переключатели (ключи), прямоугольники — это резисторы. На один из полюсов схемы подается напряжение питания, на другой — «нуль вольт».

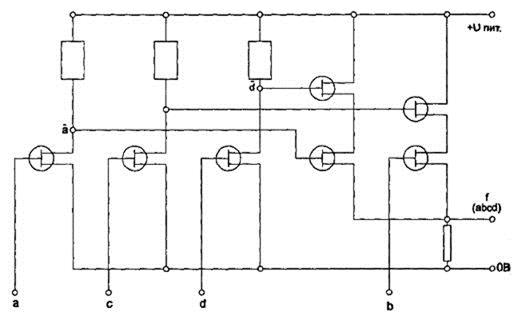
Рис. 35.Реализация ПФ транзисторной схемой

Реализация импликации может быть основана на использовании магнитных процессов. Представление функции 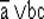в виде суперпозиции операций → выглядит следующим образом:

Переключательные схемы и схемы из функциональных элементов реализуют так называемые конечные автоматы, которые будут рассмотрены далее.