Двоичные переключательные функции и способы их задания

Функция f, зависящая от n переменных, называется двоичной переключательной (булевой ), если она и любой из ее аргументов xi, 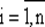принимают значение только из конечного множества, содержащего два элемента.

Таким множеством может быть бинарное множество В = {0, 1}.

Произвольная переключательная функция задается одним из способов: матричным (табличным), геометрическим, аналитическим.

При матричном способе переключательная функция f(x1, ..., хn) задается таблицей ее значений — таблицей истинности — одномерной или двухмерной (картой Карно), где указываются наборы переменных и соответствующие значения функции.

Под двоичным набором δ = á δ1, δ2, …, δnñ , δ ∈ {0, 1} понимается совокупность значений аргументов x 1, x 2, …, xnПФ.

Иногда двоичные наборы в таблицах истинности удобно представлять номерами наборов:

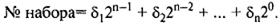
Значения функций на 2n-наборах также могут быть заданы десятичным номером:

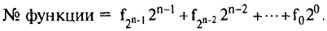
При геометрическом способе ПФ задается с помощью соответствующей отметки вершин n-мерного куба, который по сути является решеткой Хассэ, представляющей собой частично упорядоченное множество наборов (каждая вершина — точка n -мерного пространства). Каждый путь из вершины, соответствующей нулевому набору в вершину единичного набора, соответствует увеличению сравнимых наборов (рис. 28, отношение ≥).

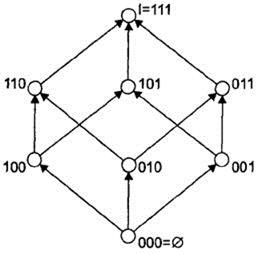
Рис. 28. Геометрическое представление переключательной функции

Этот рисунок изображает частично упорядоченное множество наборов 000, 001, 010, 011, 100, 101, 110, 111, на которых задана переключательная функция трех переменных, например, а, b , с. Вершины, на которых функция равна 1, должны быть как-то отмечены.

Переключательная функция может быть задана и некоторым словесным описанием, указывающим, на каких наборах аргументов какое значение она принимает, и исключающим неверное толкование, всякую двусмысленность. Переключательная функция может быть задана перечислением ее рабочих (единичных), запрещенных (нулевых) и условных наборов (на этих наборах функция не определена). Для упорядоченного задания n -мерных наборов переменных функции f (x 1, x 2, …, xn) удобно рассматривать их в виде целого неотрицательного числа. При этом младший разряд располагается справа. Например, для переменных х5, x 4, х3, х2, х1конкретное их значение истинности 1, 0, 0, 1, 1 соответствует двоичному числу 10011. Это число еще называют номером набора . Для компактной записи наборов значений переменных логической функции целесообразно представлять их номерами — числами в десятичной, восьмеричной, шестнадцатеричной системах счисления. Такой номер-набор называют еще весовым состоянием , или весом этого набора.

Так, 100112↔ 1910↔ 238↔ 1316, ↔ знак эквивалентности.

В случае использования десятичной системы счисления каждой переменной соответствует степень числа 2 (вес разряда) в зависимости от номера переменной, например, в порядке 2423222120. Зафиксированный порядок переменных, каждая из которых имеет свой вес, называется базой функции (старший вес — слева). Переключательная функция может быть задана таблицей истинности, которая иногда еще называется таблицей соответствия.

Таблицу истинности можно представить в двухмерном виде, который называется картой Карно (табл. 13–14).

Около карты Карно (табл. 14) иногда указываются области единичного значения переменных. Каждая клетка такой таблицы соответствует одному набору значений переменных, весовое состояние которого указано в правом верхнем углу, и в ней проставлено значение функции на таком наборе.

Таблица 13

Одномерная таблица истинности некоторой функции

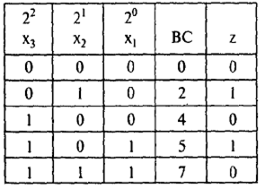
Таблица 14

Двухмерная таблица истинности

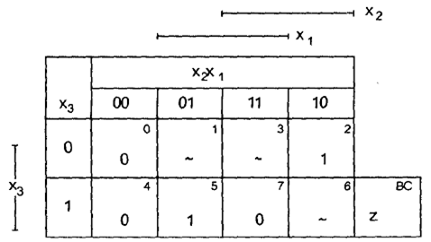
Переключательная функция может быть представлена в виде формулы, такое представление носит название аналитического. Например, переключательная функция, заданная табл. 13–14, может быть представлена формулой 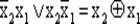, т. е. данная функция не зависит от х3.