Линейные функции двух переменных

Из табл. 28 видно, что каждая линейная функция имеет инверсную ей функцию: константа 0 — константа 1; повторение х1, х2— инверсия 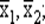сложение по модулю 2х1⊕ х2— эквиваленция х1↔ х2

5. Класс монотонных функций. Монотонная функция на большем сравнимом наборе переменных принимает не меньшие значения. Это удобно проверять на решетках Хассэ. Так, для двух переменных решетка имеет вид, как на рис. 37.

На рис. 37 проставлены значения монотонной функции х1. Видно, что 11 > 01 > 00, 11 > 10 > 00 (частично упорядоченное множество наборов).

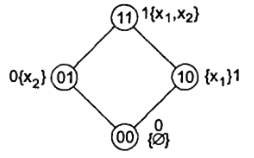
Рис. 37. Решетка Хассэ для двух переменных с указанием значений fl0( x 1x 2) = x 1

Очевидно, что константы 0, 1 — монотонные функции, дизъюнкция и конъюнкция — монотонные функции, повторения х1, х2— монотонные функции.

Система логических функций называется функционально полной , если любая произвольная переключательная функция от любого числа переменных может быть представлена в виде суперпозиции функций из этой системы.

Функционально полная система логических функций называется минимальной , если удаление из нее хотя бы одной функции превращает ее в неполную. Критерий функциональной полноты устанавливает теорема Поста, в которой утверждается, что для функциональной полноты систем переключательных функций необходимо и достаточно, чтобы они содержали следующие функции:

● не сохраняющую константу 0;

● не сохраняющую константу 1;

● несамодвойственную;

● нелинейную;

● немонотонную.