Переключательные функции от трех аргументов

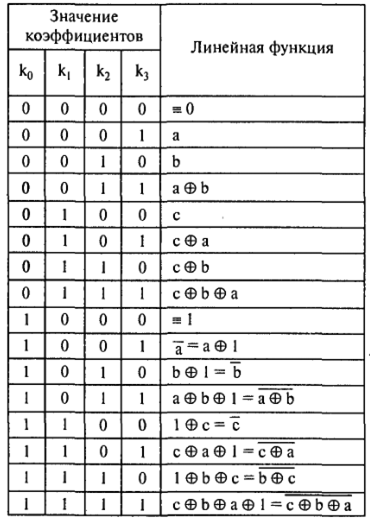
Проверим, не равна ли наша функция функциям

а ⊕ b , а ⊕ с, b ⊕ с, а ⊕ b ⊕ с и их инверсиям:

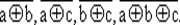
Для этого получим соответствующие векторы этих линейных ПФ (табл. 31).

Таблица 31

Векторы переключательных функций

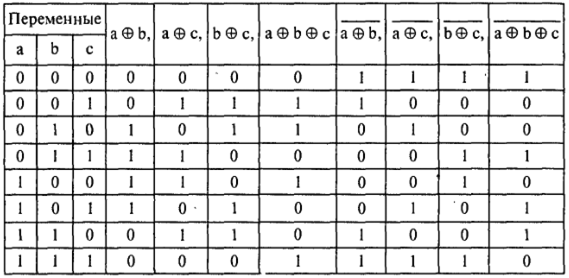
Видим, что ни один из полученных векторов этих восьми линейных ПФ не совпадает с вектором нашей функции.

Следовательно, функция № 17410— не линейная.

4. Определим, обладает ли наша ПФ свойствами самодвойственности.

Для этого проанализируем ее вектор в двоичном коде (рис. 38).

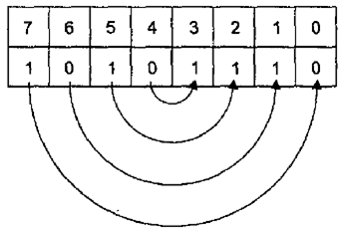
Рис. 38. Вектор в двоичном коде

Видим, что симметричные разряды 5 и 2 неортогональны. Следовательно, ПФ — несамодвойственна. У самодвойственной ПФ симметричные разряды ортогональны (противоположны).

5. Определим, монотонна ли наша ПФ.

Посмотрим на куб соседних чисел. Монотонная функция по всем возможным путям из вершины (000) в вершину (111) монотонна. Однако наша функция на наборе (010) принимает значение «1», а на большем сравнимом наборе (110) — «0». Следовательно, она не монотонна.

Представим вектор свойств ПФ (табл. 32).

Таблица 32

Вектор свойств ПФ

В восьмеричном коде вектор свойств равен 308, а в шестнадцатеричном — 1816.