Понятие о технической интерпретации конечных автоматов

В абстрактной теории автоматов существенна только работа автомата со словами при наличии конечной памяти.

Нас же более всего будет интересовать прикладная сторона теории конечных автоматов.

Конечный автомат представляет собой хотя и абстрактную, но с функциональной точки зрения довольно точную модель дискретного (цифрового) вычислительного или управляющего (контролирующего) устройства с конечным числом состояний. Входной символ (буква) — это входной сигнал, точнее комбинация (набор) сигналов на всех входах x1, x2, ..., хn(это не буквы алфавита X) устройства. Эта комбинация сигналов на дискретных входах еще называется входным вектором (набором) 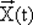. Выходной сигнал (буква) — комбинация (набор) сигналов на дискретных выходах z 1, z 2, ..., zm(это не буквы алфавита Z) — выходной вектор (набор) . Входное слово — последовательность входных векторов, поступающих в дискретные моменты времени (такты) t = 1, 2, 3...

Состоянию автомата соответствует вектор 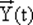— текущее, 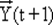— последующее. Этот вектор задает комбинация (набор) состояний y 1, y 2, ..., ys(это не буквы алфавита Y) элементов памяти автомата.

Выходное слово — последовательность выходных векторов в дискретные моменты времени.

Комбинационный автомат интерпретируется некоторой переключательной схемой или схемой из функциональных элементов (рис. 54).

Рис. 54.Техническая интерпретация комбинационного автомата

Функция выходов 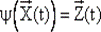(отображение 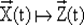) реализуется, например, с использованием функционально-полного набора элементов, соответствующих логическим функциям, составляющим функционально-полную систему. При этом представляется в виде суперпозиции этих логических функций. Вопрос представления логических функций в разных базисах и получения соответствующих схем, так же, как и вопрос получения переключательных комбинационных схем, рассматривается особо.

Последовательностный автомат интерпретируется схемой с обратными связями в виде так называемых задержек на один такт (рис. 55).

Рис. 55. Техническая интерпретация автомата Мили

Дело в том, что проблема автоматной полноты (для последовательностного автомата) алгоритмически неразрешима в отличие от проблемы полноты для переключательных функций (для комбинационного автомата).

Однако в теории конечных автоматов доказано, что последовательностный автомат может быть реализован как композиция комбинационного автомата и двоичных задержек на один такт в цепи обратной связи.

На рис. 55 ЛП — логический преобразователь — комбинационный автомат, реализующий функции переходов φ и выходов ψ, D — задержки (от слова delay — задержка). В качестве задержек могут использоваться так называемые элементы памяти.

В автомате Мура функции выходов реализуются отдельно (рис. 56), т. е. имеются два логических преобразователя (ЛП1, ЛП2).

Таким образом, в автомате Мили выходной вектор в некоторый момент времени зависит как от текущего состояния автомата, так и от входного вектора в этот момент времени.

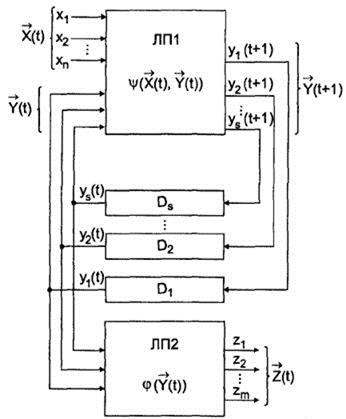
Рис. 56. Техническая интерпретация автомата Мура

В автомате Мура выходной вектор в некоторый момент времени непосредственно не зависит от входного вектора, а однозначно определяется внутренним состоянием в этот же момент времени. Поэтому автоматы Мура менее быстродействующие, чем автоматы Мили. Автоматы могут быть описаны также уравнением (функциями) переходов и выходов (аналитически).

Реальные дискретные автоматы функционируют по тактам. Такт — отрезок времени произвольной длины, в течение которого состояние автомата остается неизменным. Такты могут обозначаться моментом времени t0, t1, t2,..., tμ, причем последовательность номеров тактов образует дискретное (автоматное) время.

В теории конечных автоматов принимается допущение, что переход из одного внутреннего состояния в другое происходит скачкообразно, мгновенно. В реальных автоматах всегда имеет место конечная длительность переходных процессов.

Такты бывают устойчивыми и неустойчивыми. Такт называют устойчивым , если очередное изменение состояния автомата происходит только за счет изменения состояния входов, т. е. после поступления очередного входного набора. Такт называют неустойчивым , если очередное изменение состояния автомата происходит только за счет изменения внутреннего состояния — элементов памяти. Устойчивые такты в клетках таблицы переходов-выходов обычно отмечают кружками. Дискретные автоматы, в которых изменение внутренних состояний происходит в определенные моменты времени, определяемые специальным генератором синхронизирующих импульсов, называют синхронными . При этом, как правило, все тактовые интервалы равны.

Автоматы, в которых переходы из одного состояния в другое заранее не определены и могут совершаться в произвольные моменты времени через неравные промежутки времени, называют асинхронными .

Дискретный автомат — это устройство дискретного преобразования информации: при подаче на его вход некоторой последовательности входных наборов он формирует некоторую последовательность выходных наборов.

Для реального автомата актуальным является наиболее экономичная его реализация из всех возможных реализаций в смысле затрат элементов, энергопотребления и т. д.

Можно интерпретировать автомат не только как устройство. Известно, что всякое управление (вычисление, контрольную операцию) можно реализовать как аппаратурно (в виде устройства), так и программно (в виде программы ЭВМ). Это приводит к более общему толкованию конечных автоматов как алгоритмов с конечной памятью, многие свойства которых можно исследовать и безотносительно к способу их реализации.

Имеется еще и другая интерпретация автоматов. Фон Нейман рассматривал автоматы как удобный язык для описания основных законов взаимодействия сложных систем, т. е., по существу, как метаязык кибернетики.

Задачами теории конечных автоматов являются:

1) изучение возможностей автоматов в терминах множеств слов, с которыми они работают (распознавание входных последовательностей — слов), формирование требуемых выходных, т. е. автоматных отображений;

2) распознавание различных свойств автоматов;

3) описание автоматов (анализ) и их реализация, т. е. представление автомата как структуры, состоящей из объектов фиксированной сложности (синтез).

При синтезе автоматов выделяют следующие этапы:

1) абстрактный синтез, или формализация условий работы, когда от некоторого высокоуровневого описания автомата (например, на естественном языке — в виде словесной формулировки) переходят к математической модели. Такой моделью может быть таблица истинности для комбинационного автомата, таблица переходов-выходов для последовательностного автомата. В свою очередь по этим моделям получают переключательные функции в символической форме;

2) структурный синтез — производится минимизация переключательных функций, описывающих автомат, выполняется их представление в виде, соответствующем заданному базису реализации.

Эти два этапа называют логическим проектированием . Их результатом является функциональная схема автомата (например, функциональная электрическая схема);

3) физический синтез — решаются вопросы построения принципиальной схемы (например, принципиальной электрической схемы), создания топологии кристалла микросхемы, обеспечения надежности, помехоустойчивости и в дальнейшем изготовления автомата.

При синтезе последовательностного автомата проводится и минимизация числа состояний автомата — путем сжатия таблицы переходов-выходов.