Расстояние Хемминга

Американский математик Хемминг исследовал, от чего зависит данный код, будет ли он обнаруживать ошибки и когда может их исправлять. Интуитивно ясно, что это зависит от того, как разнесены между собой кодовые слова и сколько ошибок может появиться в передаваемом слове. M ы сейчас формализуем следующую идею. При кодировании надо согласовывать число возможных ошибок в передаваемом слове так, чтобы при изменении передаваемого кодового слова оно оставалось более близким к исходному кодовому слову, чем к любому другому кодовому слову.

Определение 13.1.Рассмотрим на множестве всех двоичных слов в алфавите В = {0,1} длины т расстояние d ( x , у ), которое равно числу несовпадающих позиций этих слов. Например, Для слов х = 011101, у = 101010 расстояние равно d ( x , y ) = 5. Это расстояние носит название расстояние Хемминга .

Можно показать, что расстояние Хемминга удовлетворяет аксиомам метрического пространства:

1) d ( x , у ) ≥ 0, d ( x , у ) = 0 тогда и только тогда, когда х = у;

2) d ( x , y ) = d ( y , x );

3) d ( x , у ) ≤ d ( x , z ) + d ( z , у ) — неравенство треугольника.

Теорема 13.1(об обнаруживающем коде ). Код является обнаруживающим в случае, когда в передаваемом слове имеется не более чем k ошибок, тогда и только тогда, когда наименьшее расстояние между кодовыми словами

d ( b 1, b 2) ≥ k + 1.

Теорема 13.2(об исправляющем коде .). Код является исправляющим все ошибки в случае, когда в передаваемом слове имеется не более k ошибок, тогда и только тогда, когда наименьшее расстояние между кодовыми словами

d ( b 1, b 2) ≥ 2k + 1.

Доказательство . Доказательства этих теорем аналогичны. Поэтому докажем только последнюю теорему.

Достаточность . Пусть для любых кодовых слов имеем d ( b 1, b 2) ≥ 2k + 1. Если при передаче кодового слова b 1произошло не более k ошибок, то для принятого слова с имеем d ( b 1, c ) ≤ k . Но из неравенства треугольника для любого другого кодового слова b 2имеем d ( b 1, с ) + d ( c , b 2) ≥ d ( b 1, b 2) ≥ 2 k + 1. Следовательно, от принятого слова до любого другого кодового слова расстояние d ( c , b 2) ≥ k + 1, т. е. больше, чем до b 1. Поэтому по принятому слову с можно однозначно найти ближайшее кодовое слово b 1и далее декодировать его.

Необходимость . От противного. Предположим, что минимальное расстояние между кодовыми словами меньше, чем 2 k + 1. Тогда найдутся два кодовых слова, расстояние между которыми будет d ( b 1, b 2) ≤ 2 k . Пусть при передаче слова b 1принятое слово с находится на отрезке между словами b 1, b 2и имеет ровно k ошибок. Тогда d ( c , b 1) = k , d ( c , b 2) = d ( b 1, b 2) – d ( c , b 1) ≤ k . Тем самым по слову с нельзя однозначно восстановить кодовое слово, которое было передано, b 1или b 2. Пришли к противоречию.

Пример 13.3. Рассмотрим следующие пятиразрядные коды слов длиной 2 в алфавите В = {0,1}:

b 1= K (00) = 00000, b 2= K (01) = 01011,

b 3= K (10) = 10101, b 4= k (11) =11110.

Минимальное расстояние между различными кодовыми словами равно d ( bi, bj) = 3. В силу первой теоремы об обнаруживающем коде, этот код способен обнаруживать не более двух ошибок в слове. В силу второй теоремы, код способен исправлять не более одной ошибки в слове.

Групповые коды

Рассмотрим подробнее коды слов в алфавите В = {0, 1}. Если для слов длиной т используются кодовые слова длиной n , то такие коды будем называть (т , п )-коды. Всего слов длиной m равно 2 m. Чтобы задать (т , п )-код, можно перечислить кодовые слова для всех возможных слов длиной m , как в предыдущем примере. Более экономным способом задания кодовых слов является матричное задание.

В этом случае задается порождающая матрица G = ∣∣ gij∣∣ порядка т × п из 0 и 1. Кодовые слова определяются каждый раз по слову а = а 1a 2... атпутем умножения этого слова слева, как вектора, на порождающую матрицу

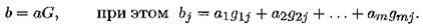
Здесь сложение определяется по модулю 2. Для того чтобы разным словам соответствовали разные кодовые слова, достаточно иметь в матрице G единичный базисный минор порядка т , например крайний левый.

Пример 13.4. Рассмотрим порождающую матрицу

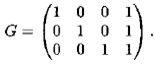
Эта матрица задает (3, 4)-код. При этом три первые символа в кодовом слове информационные, а четвертый — контрольный. Он равен 0, если четное число единиц в исходном слове, и 1, если нечетное число единиц. Например, для слова а = 101 кодом будет b = aG = 1010. Минимальное расстояние Хемминга между кодовыми словами равно d ( bi, bj) = 2. Поэтому это — код, обнаруживающий однократную ошибку.

Определение 13.2.Код называется групповым, если множество всех кодовых слов образует группу. Число единиц в слове а называется весамслова и обозначается 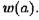Если b — кодовое слово и принятое в канале связи слово с = b + е , то слово е называется вектором ошибок.

Теорема 13.3.Пусть имеется групповой (т , п )-код. Тогда коммутативная группа К всех кодовых слов является подгруппой коммутативной группы С всех слов длины п , которые могут быть приняты в канале связи. Наименьшее расстояние между кодовыми словами равно наименьшему весу ненулевого кодового слова и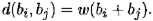

Рассмотрим фактор-группу С / K . Смежные классы здесь будут определяться сдвигом е + b , b ∈ K .

В качестве представителя смежного класса выберем элемент с наименьшим весом. Будем такие элементы называть лидерами смежного класса .

Если лидеры трактовать как векторы ошибок, то каждый смежный класс — множество искаженных слов в канале связи с фиксированным вектором ошибок, в частности при е = 0 имеем смежный класс слов без искажений, т. е. множество всех кодовых слов. Процесс коррекции и декодирования слова с заключается в поиске того смежного класса, к которому относится слово с = е + b . Вектор ошибок е определяет число и локализацию ошибок, кодовое слово b определяет коррекцию принятого слова.

Чтобы облегчить поиск смежного класса и тем самым вектора ошибок, Хемминг предложил использовать групповые коды со специальными порождающими матрицами.

Хемминговы коды

Рассмотрим построение хеммингова (т , п )-кода с наименьшим весом кодового слова равным 3, т. е. кода, исправляющего одну ошибку.

Положим п = 2 r– 1 и пусть в каждом кодовом слове будут r символов контрольными, а т символов (т = п – r = 2 r– 1– r ) — информационными, r ≥ 2, например (1, 3)-код, (4, 7)-код и т. д. При этом в каждом кодовом слове b = b 1b 2... b псимволы с индексами, равными степени 2, будут контрольными, а остальные информационными. Например, для (4, 7)-кода в кодовом слове b = b 1b 2b 3b 4b 5b 6b 7 символы b 1b 2b 4будут контрольными, а символы b 3b 5b 6b 7— информационными. Чтобы задать порождающую матрицу G хеммингова (т , п )-кода, рассмотрим вспомогательную матрицу М порядка r × п , где п = 2 r– 1, такую, что в каждом j столбце матрицы М будут стоять символы двоичного разложения числа j , например для (4, 7)-кода матрица М будет 3 × 7:

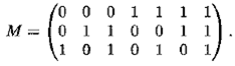
Множество всех кодовых слов зададим как множество решений однородной системы линейных алгебраических уравнений вида

b МТ= 0.

Например, для (4, 7)-кода такая система будет:

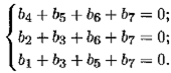
Выберем естественный базисный минор системы b МТ= 0, стоящий в столбцах с номерами, равными степени 2. Тем самым переменные разделим на базисные (кодовые) и свободные (информационные). Теперь, задав свободные переменные, легко получить базисные. Найдем фундаментальную систему m = п – r решений этой однородной системы. Тогда любое решение системы есть линейная комбинация этих m решений. Поэтому, выписав построчно m решений фундаментальной системы в виде матрицы G размером m × п , получим порождающую матрицу хеммингова группового (т , п )-кода, например для (4, 7)-кода фундаментальной системой решений будут 4 = 7 – 3 следующих решения однородной системы:

g 1= 1110000, g 2= 1001100, g 3= 0101010, g 4= 1101001.

Любая линейная комбинация этих решений будет решением, т. е. кодовым словом. Составим из этих фундаментальных решений порождающую матрицу

Теперь по любому слову а длиной т = 4 легко вычислить кодовое слово b длиной п = 7 при помощи порождающей матрицы b = aG . При этом символы b 3, b 5, b 6, b 7будут информационными. Они совпадают с а 1, а 1, а 3, а 4.Символы b 1, b 2, b 4 будут контрольными.

Вывод . Хемминговы коды удобны тем, что при декодировании легко определяются классы смежности. Пусть принятое по каналу связи слово будет с = е + b , где е — ошибка, b — кодовое слово. Тогда умножим его на вспомогательную матрицу сМТ= (е + b )МТ= еМ T. Если еМ T= 0, то слово с — кодовое и считаем: ошибки нет. Если еМ T≠ 0, то слово е определяет ошибку.

Напомним, что построенный хеммингов (т , п )-код определяет одну ошибку. Поэтому вектор ошибки е содержит одну единицу в i позиции. Причем номер i позиции получается в двоичном представлении как результат еМ T, совпадающий с i столбцом матрицы М . Осталось изменить символ i в принятом по каналу слове с, вычеркнуть контрольные символы и выписать декодированное слово.

Например, пусть принятое слово будет с = 1100011 для (4, 7)-кода Хемминга. Умножим это слово на матрицу М T. Получим

(1100011}М T=(010).

Следовательно, есть ошибка во втором символе. Поэтому кодовое слово будет b = 1000011. Вычеркнем контрольные символы b 1, b 2, b 4.Декодированное слово будет а = 0011.

Конечно, если ошибка была допущена более чем в одном символе, то этот код ее не исправит.