Основные определения теории конечных автоматов

Конечным автоматом (просто автоматом) называется система (пятерка) :

S = <X , Y , Z , φ, ψ>,

где X = {х1, х2, …, хi} — конечное входное множество (входной алфавит);

Y = {y 1, y 2, …, yj} — конечное множество внутренних состояний автомата (алфавит состояний);

Z = {z 1, z 2, …, zk} — конечное выходное множество (выходной алфавит);

φ — функция переходов (из состояния в другие состояния);

ψ — функция выходов.

Если указанные множества бесконечные, то это уже не конечный автомат.

Если функция переходов вероятностная, то это недетерминированный автомат.

Если в автомате выделено одно состояние, называемое начальным (обычно это y 1), то полученный автомат называется инициальным и обозначается <S , y >. Таким образом, по неинициальному автомату с i состояниями можно i различными способами определить инициальный автомат.

Функция переходов представляет собой отображение вида φ: X × X ↦ Y или в другом виде:

y (t + 1) = φ[x (t ), y (t )],

где x (t ), y (t ), y (t + l ) — конкретные символы алфавитов X и Y соответственно в моменты автоматного времени t , t + 1 (в тактах t и t + 1); y (t ) — текущее внутреннее состояние при соответствующем x (t ); y (t + l ) — последующее внутреннее состояние.

Иначе говоря, функция переходов определяет последующее состояние автомата по заданному текущему и входному символу.

Функция выходов представляет собой отображение вида ψ: X × Y ↦ Z или в другом виде:

z (t ) = ψ[x (t ), y (t )],

где x (t ), y (t ), z (t ) — конкретные символы алфавитов X , Y , Z соответственно. Мы не будем особо выделять последующие значения x (t + 1) и z (t + 1), поэтому зависимость от t будем указывать только для внутреннего состояния, чтобы отделять y (t ) от y (t + l ).

Указанная функция выходов — функция так называемого автомата Мили .

В теории конечных автоматов рассматривается также автомат Мура , у которого функция выходов проще: ψ: X ↦ Y или z (t ) = ψ[y (t )].

Автомат называется комбинационным , если для любого входного символа х и любых состояний уi, yj φ(х, уi) = φ(х, уj) = z , иначе говоря, если выходной символ z не зависит от состояния и определяется текущим входным символом. Говорят, что у такого частного класса автомата все состояния эквивалентны и, следовательно, комбинационный автомат имеет одно состояние. Такой автомат задается тройкой символов:

S = <X , Z , ψ>.

Рассмотрим представление конечного автомата (КА) в виде «черного ящика» (рис. 51).

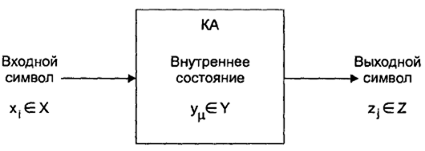
Рис. 51. Конечный автомат в виде «черного ящика»

В комбинационном автомате внутренних состояний не указывают.

Входное слово — последовательность входных символов.

Выходное слово — последовательность выходных символов, соответствующих входному слову. В конечном автомате также выделяется последовательность символов внутренних состояний, соответствующих входному слову.

Большой вклад в теорию дискретных (цифровых) автоматов внесли отечественные ученые: М.А. Гаврилов, который опубликовал первую в мире монографию «Теория релейно-контактных схем» (1950 г.), В.М. Глушков, В.Н. Рогинский, П.П. Пархоменко, В.Г. Лазарев, С.И. Баранов, А.Д. Закревский, Э.А. Якубайтис, С.В. Яблонский, В.И. Варшавский и др.

Описание конечных детерминированных автоматов
таблицами переходов-выходов и графами

Поскольку функции φ и ψ определены на конечных множествах, их можно задавать таблицами. Обычно две таблицы сводят в одну, φ × ψ: X × Y ↦ Y × Z и называют таблицей переходов-выходов, или просто таблицей переходов (автоматной таблицей). При задании автомата ориентированным графом (орграфом) его вершины сопоставляют с внутренними состояниями, а дуги — с условиями перехода из состояния в состояние. Дуги помечают входными символами автомата, а также соответствующими выходными символами, если это автомат Мили.

Рассмотрим граф переходов некоторого автомата Мили (рис. 52), X = {х1, х2}, Y = {у1, у2, y 3}, Z = {z 1, z 2, z 3}.

На графе автомата Мили (рис. 52) дуги помечаются дробью, где в числителе — входной символ, а в знаменателе — выходной символ.

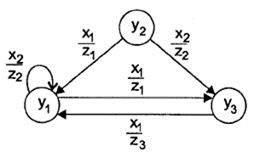
Рис. 52. Граф некоторого автомата Мили

Представим этот же автомат Мили таблицей переходов (табл. 51).

Таблица 51

Таблица переходов выходов автомата Мили,
заданного графом, представленным на рис. 52

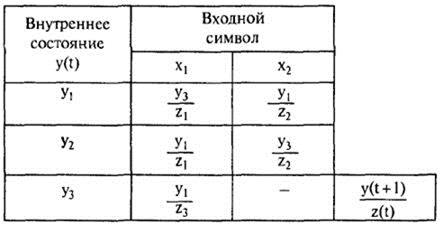
В клетках табл. 51 записывается дробь, в числителе которой указывается последующее внутреннее состояние y (t + l ), а в знаменателе — выходной символ z (t ). Это указано в специальной выноске таблицы 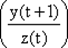. Видно, что автомат не полностью определенный (клетка у 3х 2не заполнена).

Рассмотрим граф некоторого автомата Мура (рис. 53), X = {х1, х2}, Y = {у1, у2, y 3}, Z = {z 1, z 2, z 3}:

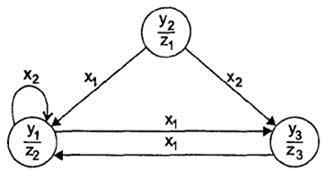
Рис. 53. Граф некоторого автомата Мура

Выходные символы в автомате Мура сопоставляются с конкретными внутренними состояниями и записываются в знаменателе дроби, помечающей внутренние состояния. Само внутреннее состояние указывается в числителе. Дуги графа автомата Мура помечаются только входными символами. Соответствующая этому автомату Мура таблица переходов представлена табл. 52.

Таблица 52

Таблица переходов выходов автомата Мура,
заданного графом, представленным на рис. 53

В клетках табл. 52, соответствующих входным символам, записывается только последующее внутреннее состояние y (t + l ), что указано в специальной сноске (y (t + l )).

Комбинационный автомат задается таблицей истинности (соответствия), уже известной нам, так как граф переходов такого автомата имеет одну вершину и m петель, где m — число входных символов. Пример таблицы истинности, задающей некоторый комбинационный автомат, приведен в табл. 53.

Таблица 53

Таблица истинности комбинационного автомата:

X ={х1, х2, х3,х4}, Z = { z 1, z 2, z 3, z 4}

В отличие от комбинационного конечного автомата, имеющего одно внутреннее состояние, конечные автоматы, имеющие больше, чем одно внутреннее состояние, называются последовательностными конечными автоматами , или просто последователъностными автоматами .

Рассмотрим последовательностный автомат, заданный табл. 54. Зафиксируем начальное состояние y 1и каждому входному слову (последовательности входных символов) 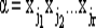поставим в соответствие слово ω в выходном алфавите:

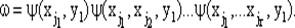
Это соответствие, отображающее входные слова в выходные, называется автоматным отображением .

Таблица 54

Таблица переходов-выходов некоторого автомата Мили

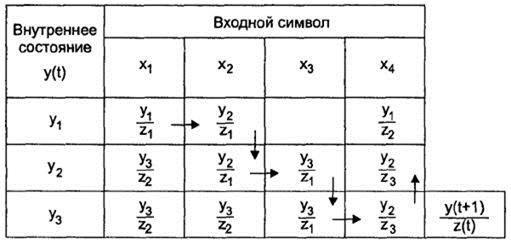
Зададим входное слово а = x1х2х3х4. Тогда выходное слово ω = z 1z 1z 1z 3.

Рассмотрим подробнее процесс формирования выходного слова:

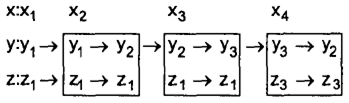
В этой последовательности указаны так называемые переходы из состояния в состояние, обведенные линией. Например, при поступлении х2автомат сначала находится в состоянии y1, а затем переходит в состояние у2. Указанные выше последовательности иногда изображают стрелками в таблице переходов-выходов.

Состояния yjназывают достижимыми из состояния yi, если существует входное слово α, такое, что φ(α, yi) = yj.

Состояния называются эквивалентными , если они соответствуют одинаковым последовательностям «входное слово — выходное слово»; причем длина такой последовательности может быть любая ≥ 1.

Автомат называется сильно связанным , если из любого его состояния достижимо любое другое состояние.

Автомат называется автономным , если его входной алфавит состоит из одной буквы X = {х}. Все входные слова автономного автомата имеют вид хх…х.