Синтез автомата-распознавателя последовательности

Дано: кодовая последовательность 0-1-3-2 двоичного двухразрядного сигнала (в десятичном коде).

Требуется получить ПФ, описывающие соответствующий конечный автомат-распознаватель последовательности (рис. 75).

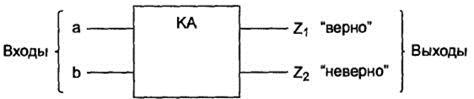
Рис. 75. Распознаватель последовательности на входах a, b

Последовательность поступает на входы a, b конечного автомата (КА):

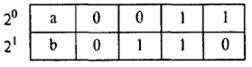
Это правильная последовательность изменения входов а, b в соответствии с заданием.

Возможны и неправильные последовательности из алфавита А = {0, 1, 2, 3}. Ограничим возможные неправильные коды изменением только одного двоичного разряда.

Рассмотрим соответствующий квадрат соседних чисел (рис. 76, так как всего два входа).

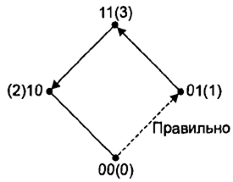
Рис. 76. Иллюстрация изменения входов

Направление изменения входных кодов показано стрелками. Видно, что вначале из 00 (0) имеем переход в 01 (1), если последовательность правильная. Если последовательность неправильная, тогда возможен лишь один вариант (рис. 77).

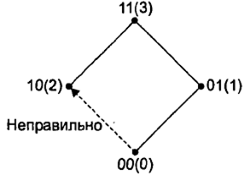
Рис. 77. Иллюстрация возможного нарушения последовательности: из 00(0) в 10(2)

На втором шаге правильно: 01 (1) в 11 (3), а неправильно (рис. 78), т. е. возможен возврат в 00.

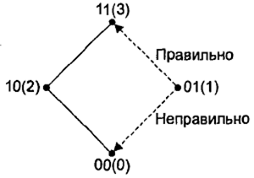
Рис. 78. Иллюстрация возможного нарушения последовательности: из 01(1) в 00(0)

Аналогично на третьем шаге неправильным будет переход из 11 (3) в 01 (1) (рис. 79).

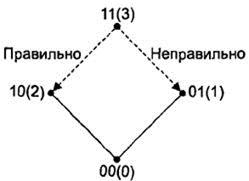
Рис. 79. Иллюстрация возможного нарушения последовательности: из 11(3) в 01(1)

Таким образом, можно построить граф возможных последовательностей (рис. 80).

Рис. 80. Граф последовательностей распознавателя 0-1-3-2

Таким образом, имеем всего 4 последовательности:

Строим первичную таблицу переходов (ПТП) соответствующего конечного автомата-распознавателя последовательности 0-1-3-2 (табл. 63).

Таблица 63

Первичная таблица переходов-выходов распознавателя 0-1-3-2

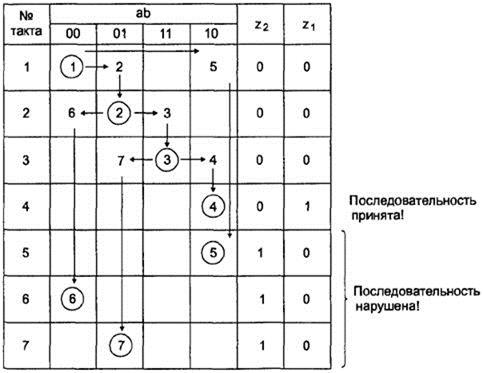
Здесь (см. табл. 63) кружком обведены устойчивые такты работы автомата-распознавателя. Переход от одного устойчивого такта в соответствующей строке таблицы переходов-выходов к другому осуществляется через неустойчивый такт. В каждой строке ПТП только один устойчивый такт, номер которого соответствует номеру строки.

Цит. по: Дискретная математика и математическая логика: учебник /
Ю.А. Аляев, С.Ф. Тюрин. — М.: Финансы и статистика, 2006. — С. 157–189.