Синтез методом каскадов

При синтезе комбинационных автоматов используется метод каскадов, основанный на разложении Шеннона:

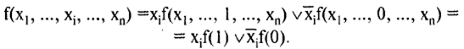
Такое разложение позволяет исключать переменные и понижать размерность по каскадам до тех пор, пока остаточные функции не будут иметь простой вид и их реализация не будет представлять трудности.

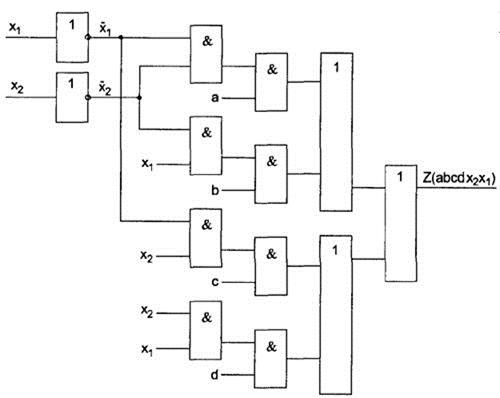
Рис. 61. Схема с учетом наличия только двухвходовых элементов И , ИЛИ

Реализуем вышерассмотренную функцию z(abcdx2x1) методом каскадов с использованием блоков исключения переменной 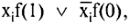которые легко реализуются в базисе И, ИЛИ, НЕ.

Очевидно, что

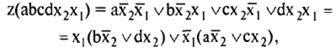
т. е. 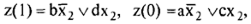которые реализуются на двухвходовых элементах И, ИЛИ. Проводить дальнейшее разложение нет необходимости. Соответствующая схема комбинационного автомата изображена на рис. 62.

Интересно, что схема на рис. 62, построенная по методу каскадов, проще в смысле числа элементов — для ее построения необходимо 11 элементов (9 двухвходовых и 2 инвертора). Сравните ее со схемой на рис. 61, для построения которой потребовалось 13 элементов (11 двухвходовых и 2 инвертора).

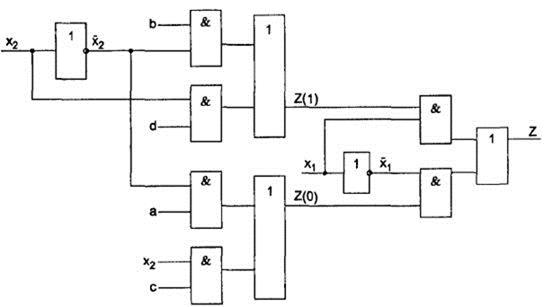
Рис. 62. Схема , построенная по методу каскадов

В общем случае сложность остаточных функций зависит от порядка исключения переменных, и оптимальное их исключение ищут специальными методами, основанными на понятии булевой производной:

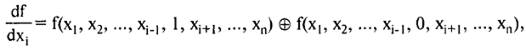
где ⊕ — сумма по модулю 2.

При использовании базисов, отличных от рассмотренного базиса И, ИЛИ, НЕ, блоки исключения переменных и блоки реализации остаточных функций реализуются в заданном базисе.