Алгоритм решения задач ЛП графическим методом

Шаг 1. В системе ограничений задачи ЛП заменить знаки неравенств на знаки точных равенств и построить соответствующие прямые.

Шаг 2. Найти и заштриховать полуплоскости, разрешенные каждым из ограничений-неравенств задачи ЛП. Для этого необходимо подставить в конкретное неравенство координаты какой-либо точки (например, (0;0)), и проверьте истинность полученного неравенства.

Если неравенство истинное,

то надо заштриховать полуплоскость, содержащую данную точку;

иначе (неравенство ложное) надо заштриховать полуплоскость, не содержащую данную точку.

Поскольку x₁ и x₂ должны быть неотрицательными, то их допустимые значения всегда будут находиться выше оси x₁ и правее оси x₂.

Ограничения-равенства разрешают только те точки, которые лежат на соответствующей прямой, поэтому необходимо выделить на графике такие прямые.

Шаг 3. Определить область допустимых решений как часть плоскости, принадлежащую одновременно всем разрешенным областям, и выделить ее. При отсутствии области допустимых решений задача не имеет решений.

Шаг 4. Если область допустимых решений – не пустое множество, то построить целевую прямую, т.е. любую из линий уровня 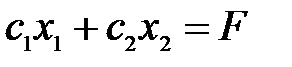, где F – произвольное число.

Шаг 5. Построить вектор 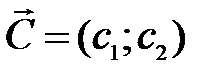, который начинается в точке (0;0), заканчивается в точке 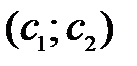. Если целевая прямая и вектор 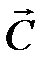построены верно, то они будут перпендикулярны.

Шаг 6. При поиске максимума целевой функции необходимо передвигать целевую прямую в направлении вектора 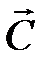, при поиске минимума целевой функции – против направления вектора 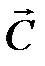. Последняя по ходу движения вершина области допустимых решений будет точкой max или min целевой функции. Если такой точки (точек) не существует, то целевая функция не ограничена на множестве планов сверху (при поиске max) или снизу (при поиске min).

Шаг 7. Определить координаты точки max (min) целевой функции 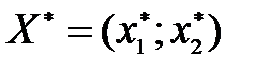и вычислить значение самой целевой функции F(X^*). Для вычисления координат оптимальной точки X^* необходимо решить систему уравнений прямых, на пересечении которых находится X^*.