Пример составления математической модели задачи
Пример №1.1. Составить математическую модель задачи.
Для производства компьютерных столов I-го и II-го видов требуются три типа ресурсов: дерево, пластик и трудозатраты. Потребности в ресурсах для производства одного стола каждого вида, запасы ресурсов, а также прибыль от реализации одного стола каждого вида, заданы в таблице 1.1.:
Таблица 1.1. – Исходные данные
| Тип ресурса | Единица продукции I-го вида | Единица продукции II-го вида | Запас ресурса |
| Дерево (м2) | |||
| Пластик (м2) | |||
| Трудозатраты (чел/час) | |||
| Прибыль (руб.) |
Необходимо найти план выпуска продукции, позволяющий получить наибольшую прибыль.
Решение.
Пусть x1 и x2 – количество продукции I-го и II-го вида соответственно.
Тогда условия – ограничения для каждого вида продукции составляются следующим образом: т.к. план выпуска продукции необходимо составлять в пределах имеющегося запаса ресурса, то расход каждого типа ресурса должен быть не более установленного предела, либо строго этот предел.
Поэтому:
условие – ограничение по дереву имеет вид:
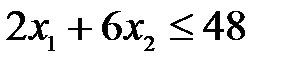 ,
,
условие – ограничение по пластику:
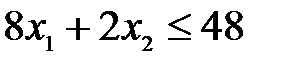 ,
,
условие – ограничение по трудозатратам:
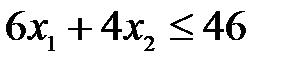 .
.
Кроме того, переменные x1, x2 должны быть больше или равны нулю:
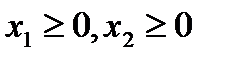 .
.
Прибыль при реализации продукции составит:
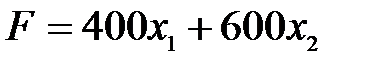 (руб).
(руб).
Т.к. прибыль должна быть максимальной, то необходимо найти максимум функции цели 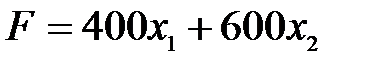 .
.
Ответ.
Математическая модель задачи имеет вид:
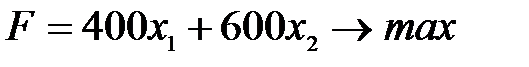
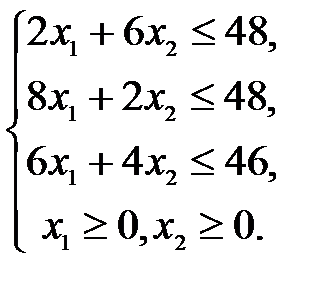
После расчета данной математической модели (ее решения) определяются значения x1, x2, удовлетворяющие системе ограничений и доставляющие максимум функции цели, т.е. рассчитывается количество производимой продукции каждого вида, необходимое для получения максимальной прибыли в условиях заданных запасов ресурсов.
Пример №1.2. Составить математическую модель задачи.
Фабрика производит два вида мыла: хозяйственное и туалетное. Продукция обоих видов поступает в оптовую продажу. Для производства мыла используются два ингредиента – А и В. Максимально возможные суточные запасы этих ингредиентов составляют 6 т и 8 т соответственно. Известны расходы ингридиентов А и В на 1 т соответствующих видов мыла (табл. 1.2.). Изучение рынка сбыта показало, что суточный спрос на туалетное мыло никогда не превышает спроса на хозяйственное мыло более, чем на 1 т. Кроме того, установлено, что спрос на туалетное мыло никогда не превышает 2 т в сутки. Оптовая цена одной тонны хозяйственного мыла равна 3 тыс. руб., а одной тонны туалетного мыла – 2 тыс. руб.
Таблица 1.2. – Исходные данные
| Ингредиенты | Расход ингредиентов, т ингр./т мыло | Запас, т ингр./сутки | |
| Хозяйственное мыло | Туаленое мыло | ||
| А | |||
| В |
Необходимо построить математическую модель, позволяющую установить, какое количество мыла каждого вида надо производить, чтобы доход от реализации продукции был максимальным.
Решение.
Пусть x1 – количество хозяйственного мыла,
x2 – количество туалетного мыла.
Запись условий – ограничений:
для ингредиента А в условиях запаса:
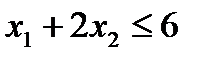 (т ингр.А/сутки),
(т ингр.А/сутки),
для ингредиента В в условиях запаса:
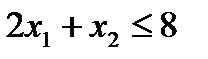 (т ингр.В/сутки),
(т ингр.В/сутки),
суточный спрос обоих ингредиентов:
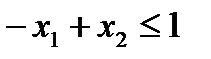 (т мыла/сутки),
(т мыла/сутки),
суточный спрос туалетного мыла:
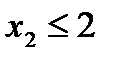 (т мыла/сутки).
(т мыла/сутки).
Переменные x1, x2 должны быть больше или равны нулю:
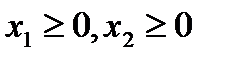 .
.
Формирование функции цели:
доход от реализации продукции составит:
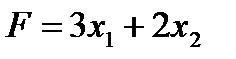 (руб. /сутки).
(руб. /сутки).
Ответ.
Математическая модель задачи имеет вид:
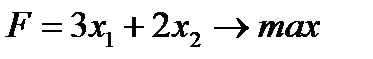
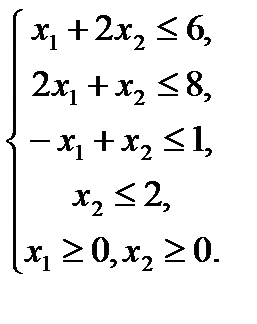
Дата добавления: 2016-04-02; просмотров: 3491;
