ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Графический метод довольно прост и нагляден для решения задачи ЛП с двумя переменными. Он основан на геометрическом представлении допустимых решений и целевой функции задачи.

Каждое из неравенств задачи ЛП определяет на координатной плоскости (x₁, x₂) некоторую полуплоскость (рис.2.1), а система неравенств в целом – пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений.

Область допустимых решений всегда представляет собой выпуклуюфигуру, т.е. обладающую следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей.

Область допустимых решений графически может быть представлена:

- выпуклым многоугольником,

- неограниченной выпуклой многоугольной областью,

- отрезком,

- лучем,

- одной точкой.

В случае несовместности системы ограничений задачи ЛП область допустимых решений является пустым множеством.

Целевая функция 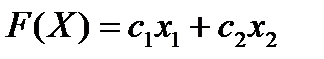при фиксированном значении 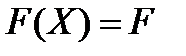определяет на плоскости прямую линию 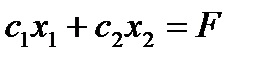. Изменяя значения F формируется семейство параллельных прямых, называемых линиями уровня.

Это связано с тем, что изменение значения F повлечет изменение лишь длины отрезка, отсекаемого линией уровня на оси x₂ (начальная ордината), а угловой коэффициент прямой 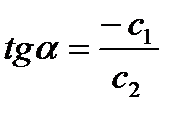останется постоянным (рис.2.1). Поэтому для решения будет достаточно построить одну из линий уровня, произвольно выбрав значение F.

Вектор 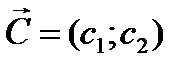с координатами из коэффициентов целевой функции при x₁ и x₂ перпендикулярен к каждой из линий уровня (рис.2.1).

Направление вектора 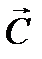совпадает с направлением возрастания целевой функции. Направление убывания целевой функции противоположнонаправлению вектора .

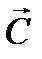Суть графического метода заключается в следующем. По направлению или против направления вектора 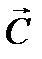в области допустимых решений производится поиск оптимальной точки 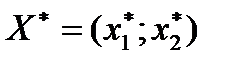. Оптимальной считается точка, через которую проходит линия уровня F_max(F_min), соответствующая наибольшему или наименьшему значению функции F(X). Оптимальное решение всегда находится на границе области допустимых решений. Например, в последней вершине многоугольника области допустимых решений, через которую пройдет целевая прямая, или на всей его стороне.

При поиске оптимального решения задачи ЛП возможны следующие ситуации:

1) существует единственное решение задачи;

2) существует бесконечное множество решений (альтернативный оптиум);

3) целевая функция не ограничена;

4) область допустимых решений – единственная точка;

5) задача не имеет решений.

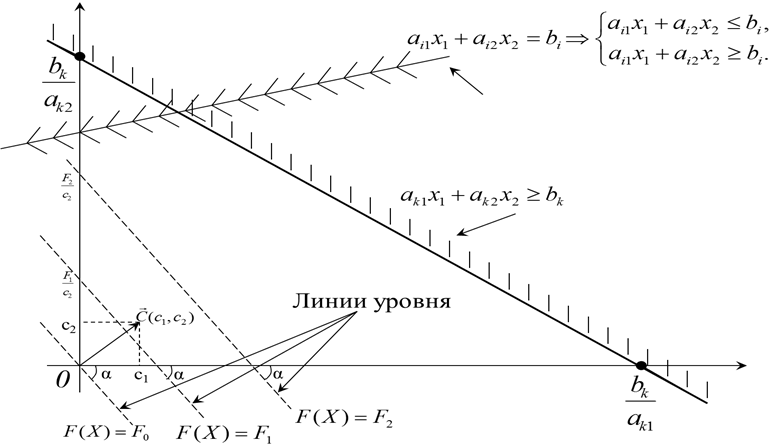
Рис. 2.1. Геометрическая интерпретация ограничений и целевой функции задачи ЛП