Правила приведения задачи ЛП к каноническому виду

1.Если условие–ограничение представляет собой неравенство со знаком ≤, то от него можно перейти к равенству, введя в левую часть ограничения дополнительную неотрицательную переменную.

Пример.

Условие ограничение в стандартной форме: ,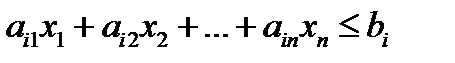

в канонической форме: ,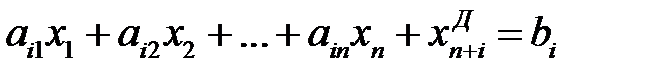

при этом .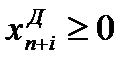

2.Если условие–ограничение представляет собой неравенство со знаком ≥, то от него можно перейти к равенству, введя в левую часть дополнительную переменную со знаком минус.

Пример.

Условие ограничение в стандартной форме: ,

в канонической форме: ,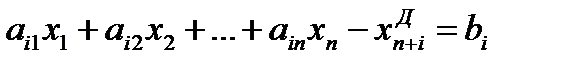

при этом .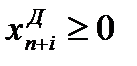

3.Функция цели приводится к каноническому виду путем добавления в нее всех дополнительных переменных, входящих в систему ограничений, с коэффициентом 0.

Пример.

Функция цели в стандартной форме: F=c₁x₁+c₂x₂+c₃x₃+…+c_nx_n→max(min),

в канонической форме:

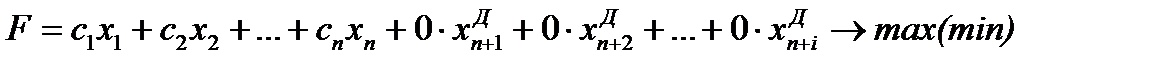
Пример приведения математической модели задачи ЛП

К каноническому виду

Пример №3.1.

Записать представленную математическую модель в каконическом виде.

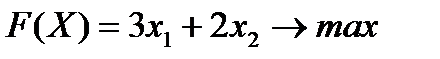
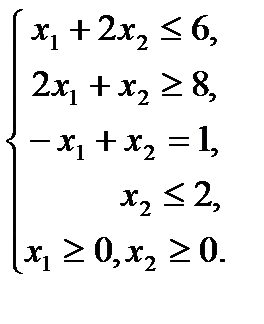
Решение.

Первое условие–ограничение представляет собой неравенство со знаком ≤. От него можно перейти к равенству, введя в левую часть ограничения дополнительную неотрицательную переменную:

.

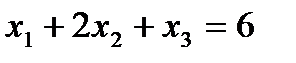Второе условие–ограничение представляет собой неравенство со знаком ≥. От него можно перейти к равенству, введя в левую часть дополнительную переменную со знаком минус:

.

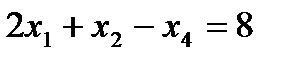Третье условие–ограничение представляет собой равенство. Его следует оставить без изменений.

Четвертое условие–ограничение представляет собой неравенство со знаком ≤. От него можно перейти к равенству, введя в левую часть ограничения дополнительную неотрицательную переменную:

.

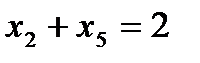Функция цели приводится к каноническому виду путем добавления в нее всех дополнительных переменных, входящих в систему ограничений, с коэффициентом 0:

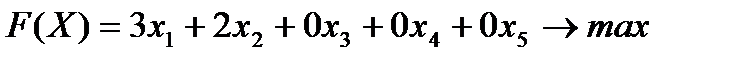
Ответ.

Математическая модель в каноническом виде имеет следующий вид:

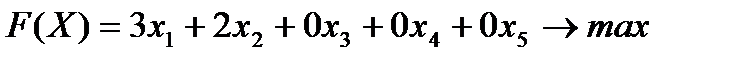
Симплексный метод является методом упорядоченного перебора решений системы ограничений, при условии, что каждое следующее решение улучшает значение функции цели.

Симплексный метод включает в себя 2 этапа:

1) определение начального допустимого базисного решения системы ограничений и функции цели;

2) последовательное улучшение начального решения и получение оптимального.

В качестве базисных переменных необходимо выбирать (если возможно) такие m переменных, каждая из которых входит только в одно условие–ограничение с коэффициентом +1 и в остальные n-m условий–ограничений с коэффициентом 0.